以上介绍了传递函数综合法的原理和步骤。在实际运用中,其实还会遇到各种问题。例如在图4.11所示的例子中,我们只考虑到了平移运动,实际中,结合点肯定还存在回转自由度。也就是说,严密的建模应该把回转自由度也考虑进来。但是,由于在回转方向上加振并测量回转方向响应的实验很困难,一般的做法是忽略掉回转自由度的影响,这就会引起误差。
传递函数矩阵是频率的函数,在某些频率上(如反共振频率上),由于测量误差的影响,传递函数矩阵可能接近病态矩阵,一般的矩阵逆运算会带来较大的数值误差。为了改进计算精度,可以利用特异值分解的方法来求逆矩阵(参见5.4.5节)。
最不好处理的情况是,子结构与主体结构之间不是通过弹性元件相结合,而是直接用螺钉连接起来,如图4.14所示。因为是面接触,理论上有无限个结合点,如何通过测量有限个传递函数来代表子结构的动特性是一个困难的工作。不严密但实用的处理方法是认为只在每个螺钉位置存在结合,这样,传递函数的测量工作仅限于各个螺钉位置,易于操作。但是,当螺钉个数很多时,测量工作量将很大,这些困难都会影响传递函数综合法的应用。
当子结构的结合面变形相对于其他部位来说很小,可以认为是刚体时(如法兰盘较厚的情况),可以近似地用一个等价结合点的6个刚体自由度(3个平移,3个回转)来代表结合面的特性。这样,只要构成6×6阶传递函数矩阵即可。由于回转响应不能直接测量,可以通过测量若干个点的平移方向的响应(如4点×3方向),根据刚体运动的法则,运用最小二乘原理来估算出等价结合点的平移及回转响应。需要指出的是,当使用工程单位(mm,kgf,s)时,平移刚性与回转刚性在数值上可能相差巨大,从而引起数值计算误差。使用国际标准单位(m,N,s)可以有效地减少这个误差。(https://www.xing528.com)
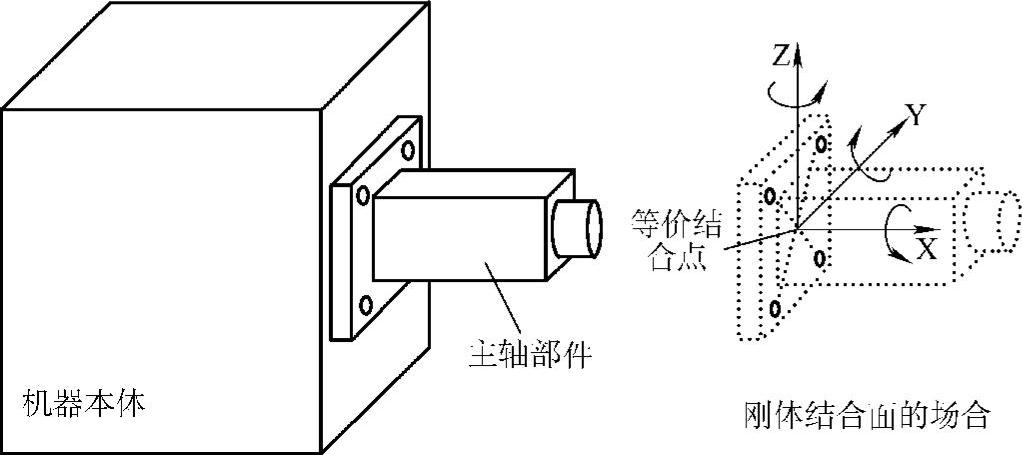
图4.14 子结构与主体结构固结的情况
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




