基于子结构模态综合法的基本思路

子结构模态综合法的思路是：把整体结构分割为若干子结构，各子结构结合部的自由度称为边界自由度，子结构内部节点的自由度称为内部自由度。对每个子结构来说，边界自由度属于A-集，内部自由度属于O-集。运用Craig-Bampton缩减法进行缩聚，可以得到各个子结构在其G-集自由度上的质量和刚性矩阵。G-集自由度是指A-集自由度与导入的固定边界模态自由度的集合。所有子结构的G-集自由度放在一起，构成了所要求解的对象结构，称为剩余结构（Residual Struc-ture）。剩余结构的质量和刚性矩阵可以由各个子结构的对应结果组装而成。

图4.4所示为子结构模态综合法的示意图。各个子结构相互独立，可以单独处理。这是最简单的情况。对于一个子结构包含另一个子结构的复杂情况，这里不予讨论。显然，在结构修改分析中，只对有变动的子结构进行重新计算即可，从而可以大大提高分析的效率。

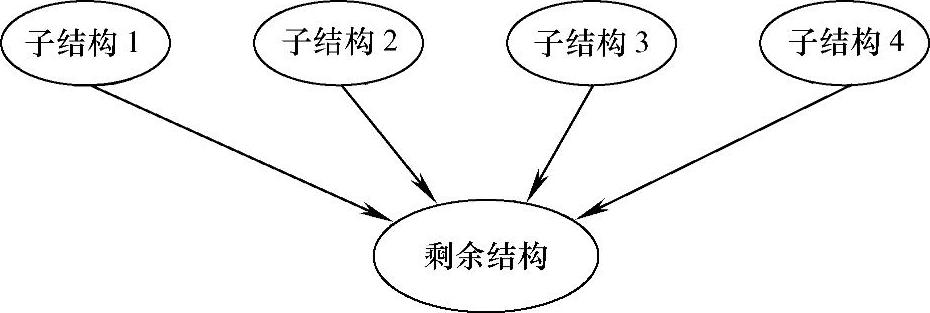
图4.4 子结构模态综合法的示意图

这里，我们以如图4.5所示的三自由度系统为例，来说明子结构模态综合法的步骤。

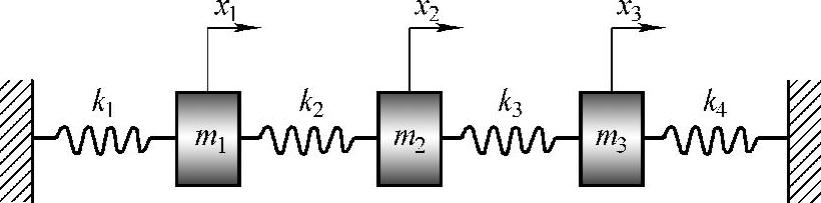
图4.5 一个三自由度系统

在应用子结构模态综合法之前，先来看看该系统的固有值的真值。为了方便起见，假设各个质量和弹簧系数的值均为1，则系统的质量和刚性矩阵为（参见3.1节的内容）

通过求解特征方程[k]-ω²[m]=0，可得系统的3个固有频率为

ω₁=0.765，ω₂=1.414，ω₃=1.848

现在来应用子结构模态综合法求解。把该系统分割为两个子结构，如图4.6所示。两个子结构的边界点为节点2，因此这个点对于子结构来说属于外点。以下分别对每个子结构的处理进行说明。

图4.6 子结构的划分

1.子结构1的处理

子结构1包括内部节点1和外部节点2。节点1处的质量和与其相连的两个弹簧是该子结构的物理构成，节点2处的质量属于剩余结构。因此，可以写出子结构1的质量和刚性矩阵为

与A-集自由度（x₂）和O-集自由度（x₁）相对应，对刚性矩阵进行划分，可以得到

[k_oo]=[2]，[k_oa]=[-1]

于是根据Guyan缩减公式（4.11），可以得到子结构1的一个Guyan模态为

x₁=[G]=-[k_oo]^-1[k_oa]=0.5

即将外部节点（x₂）强制移动一个单位位移时，内部节点（x₁）的位移为0.5。这个结果也可以由以下静力平衡方程的求解得到

其中，F为外部节点x₂=1时在该点上产生的反力。

接着来看子结构1的固定边界模态。这可以由求解以下方程得到

（[k_oo]-ω²[m_oo]）{ϕ}=0

将[k_oo]=[2]，[m_oo]=[1]代入，可得ω²=2，{ϕ}=1（质量正规化后的模态）。事实上，将外部节点（x₂）约束住后，得到的就是一个单自由度系统，只有一个模态。

在经过以上处理之后，根据Craig-Bampton变换式（4.17），得到以下变换矩阵

列数代表保留到剩余结构中去的自由度（G-集自由度），行数代表子结构的自由度数。这里，q代表固定边界模态的自由度。

于是，可以得到子结构1缩减后的刚性和质量矩阵为(www.xing528.com)

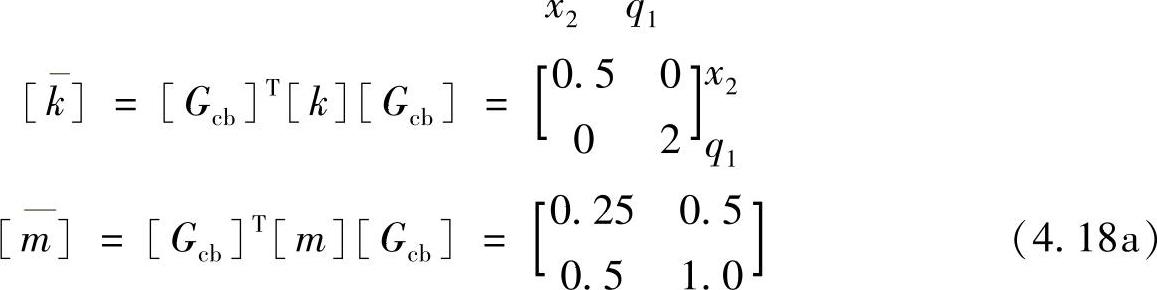
2.子结构2的处理

子结构2包括内部节点3和外部节点2。节点3处的质量和与其相连的两个弹簧是该子结构的物理构成，节点2处的质量属于剩余结构。因此，可以写出子结构2的质量和刚性矩阵为

经过同样的处理（Guyan模态和固定边界模态求解），可以得到该子结构的Craig-Bampton变换矩阵为（与子结构不同的是，这里，A—集在前，O—集在后）

于是，可以得到子结构2缩减后的刚性和质量矩阵为

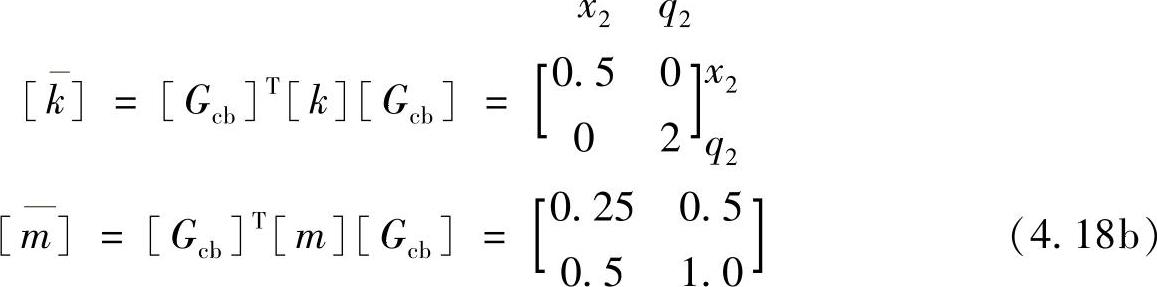
3.剩余结构的组装

剩余结构的自由度包括子结构的边界点和引入的子结构的固定边界模态自由度，总共有3个自由度，如图4.7所示。该系统中没有弹簧，只有节点2处的质量。因此，物理意义上的刚性和质量矩阵为

但是，在子结构的缩减处理过程中，我们得到了各子结构在剩余结构自由度上的等价刚性和等价质量特性。还应该把这些特性组装到上列矩阵中去，才能得到真正的剩余结构的刚性和质量矩阵。

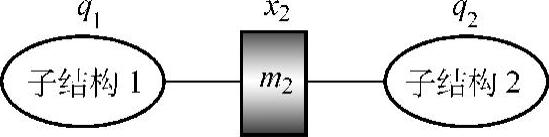
图4.7 剩余结构的构成

首先，考虑把子结构1的结果组装进来。式（4.18a）所示的结果对应于自由度x₂、q₁，把它们加到式（4.18c）所示矩阵的对应元素上去，得到的结果如下

然后，把对应于自由度x₂、q₂的子结构2的结果式（4.18b）组装进来，得到最终结果为

式（4.18e）是剩余结构的刚性和质量矩阵，求解与之相对应的特征值问题

（[k]-ω²[m]）{ϕ}=0

可以得到固有频率为ω₁=0.765，ω₂=1.414，ω₃=1.848。这与直接求解原有系统的特征方程得到的结果相同。另外，还可以得到剩余结构的模态矩阵为

最后，对子结构内部节点的还原计算做一个简单说明。从上面式（4.18f）所示的结果可以得到，子结构1和子结构2的G-集自由度上的模态向量矩阵为

利用相应的Craig-Bampton变换矩阵，可以计算得到两个子结构上所有点的模态向量

也就得到了整体结构的模态向量。在得到各种模态参数后，如果需要的话，可以进一步利用模态法计算结构的动态响应。

在这个简单的例子中，所有的固定边界模态自由度均被引入到了Craig-Bamp-ton缩减中去，因此在精度上没有损失。在实际中应用子结构模态综合法时，总是要舍去相当部分的高频模态，因此会产生一定的误差。

由于这个方法中引入了边界固定的模态自由度，所以也称为固定边界模态法。另外还有采用边界不固定的自由边界模态（Free Interface Modes）的方法，这里不做进一步说明。