Craig-Bampton缩减方法

鉴于Guyan缩减法在处理动力学方程时所带来的精度损失问题，人们又开发出了许多动力缩减方法（Dynamic Reduction），其中最有代表性的就是所谓的Craig-Bampton法。其原理是基于结构力学中著名的瑞利-利兹方法（Rayleigh-Ritz Meth-od）：结构的位移场可以由有限个含有独立系数的变形函数来逼近，这些变形函数可以任意选取，只要能满足边界条件即可。这些独立的系数也叫做广义坐标。所采用的变形函数的个数越多，即广义坐标数越多，逼近的精度越高。当广义坐标的个数与系统自由度数相等时，误差为0。这个方法是利用离散模型逼近连续体力学结构的基本原理。

事实上，Guyan缩减法也是基于这个原理。考察式（4.13），把{x_a}作为这里所说的系数（广义坐标），把由Guyan模态构成的矩阵[G_g]作为这里所说的有限个变形函数，则结果{x}就是对结构位移场的近似。显然，选取的A-集自由度的个数越多，精度越高。如果把所有的自由度都纳入A-集，则相当于没有缩减，精度不损失。由于模型缩减方法本质上相当于对原有系统增加了“看不见的约束”，因此缩减后的模型会变“刚”，这就是用Guyan缩减法计算出的固有频率偏大的原因。

作为对静态缩减法的改进，Craig-Bampton法在O-集自由度的强制变形（Guy-an模态）的基础上，引入了由O-集自由度构成的子系统在其边界固定的条件下得到的固有模态（Fixed Interface Modes），从而构成以下变换关系

{x_o}=[G]{x_a}+[ϕ]{q}（4.16）这里，[ϕ]为固定边界条件下的O-集子系统的模态矩阵，{q}为对应的模态坐标。如果将所有的模态都引入以上计算，则式（4.16）严格成立，精度不会损失（相当于没有缩减）。由于引入有限个固有模态的个数即可大大改善精度，因此在无需很多A-集自由度的情况下，仍可以达到较高的计算精度，从而实现计算精度与计算速度的“两全其美”。

综上所述，Craig-Bampton缩减法可以表示为

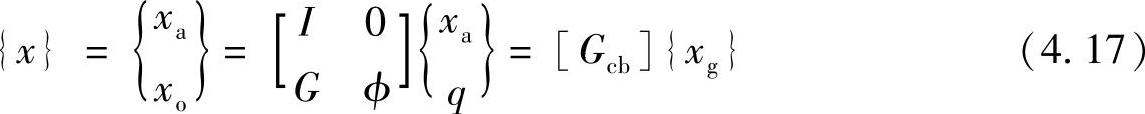
其中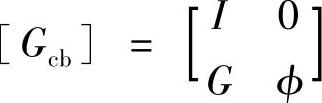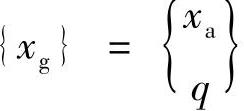，，分别为变换矩阵与广义坐标。代入到式（4.12），可得

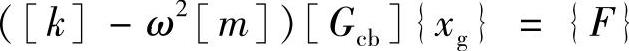
给上式两边同乘以[G_cb]^T，得到缩减后的动力学方程为

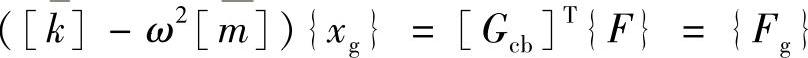
这里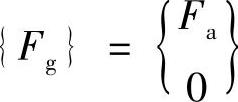，为扩展外力向量，缩减后的刚性矩阵与质量矩阵分别为

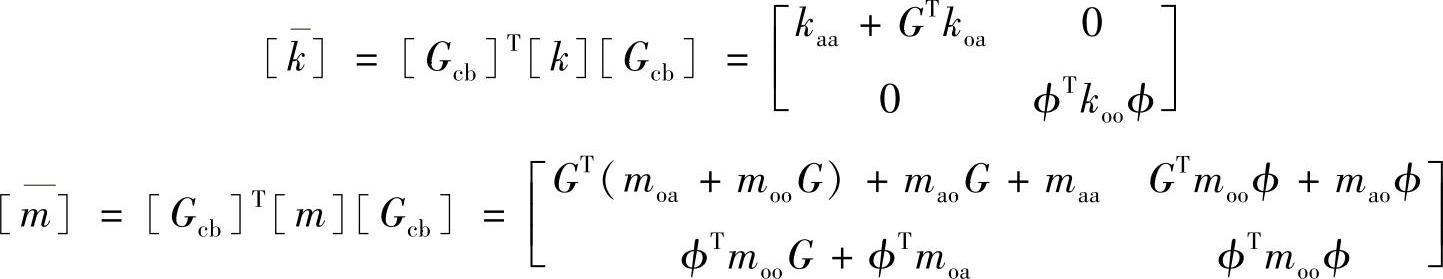
下面，我们以第3章中的悬臂梁（见图3.14）为例，来具体说明Craig-Bampton法的步骤。该悬臂梁模型共有20个没有约束的节点，每个节点具有Y方向平移和绕Z轴旋转的2个自由度，总共有40个自由度。现在把右端点的2个自由度选作要分析的A-集自由度，其余的38个自由度纳入O-集，我们来看如何应用Craig-Bampton法把原有的40个联立方程的求解问题缩聚为2+q个联立方程的求解问题。

首先，求解在每个A-集自由度上施加单位强制运动时的O-集自由度上的变形，即Guyan模态。具体到这个例子，先把右端点的绕Z轴旋转的自由度约束住，然后在Y方向施加单位位移，得到O-集自由度上的变形如图4.1a所示，这是第一个Guyan模态。接着，把右端点的Y方向的平移约束住，给绕Z轴旋转的自由度施加一个单位转角，得到如图4.1b所示的变形，这是第二个Guyan模态。由于这里的A-集只有两个自由度，相应地，只有两个Guyan模态。

图4.1 悬臂梁的两个Guyan模态(www.xing528.com)

a）第一个Guyan模态 b）第二个Guyan模态

接着，求解以下方程

（[k_oo]-ω²[m_oo]）{ϕ}=0

得到右端点被固定后的O-集自由度的固有模态（Fixed-boundary Normal Modes）。这里给出前4阶模态的形状如图4.2所示。

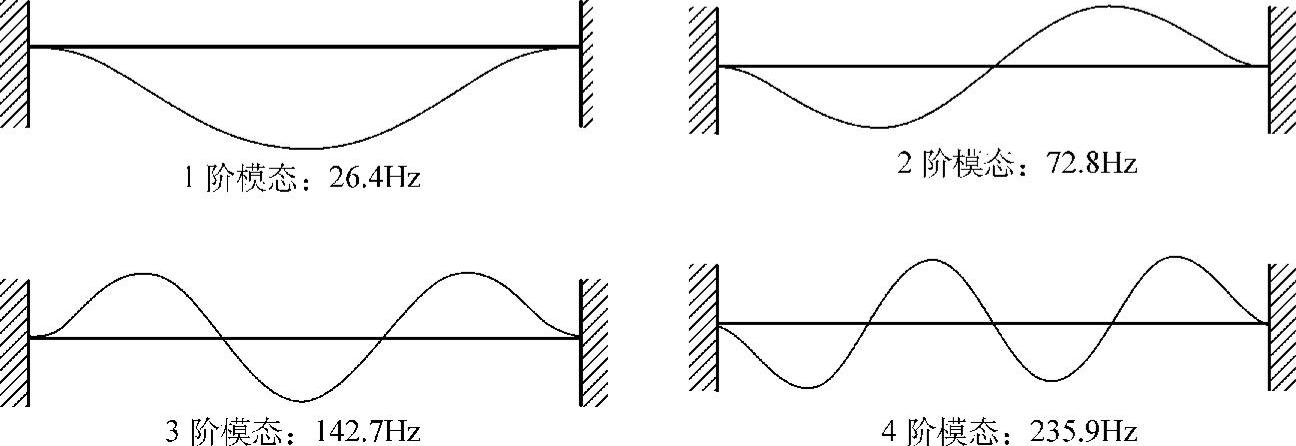
图4.2 固定边界条件下的固有模态

用以上得到的两个Guyan模态和四个固定边界条件下的固有模态，来构成以下Craig-Bampton变换矩阵

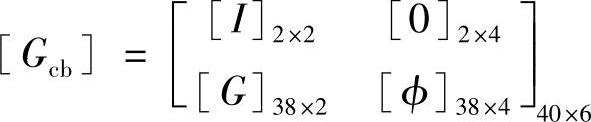
于是，得到缩聚后的运动方程为

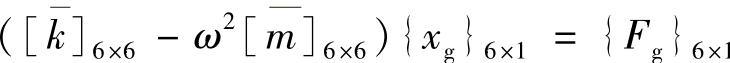
其中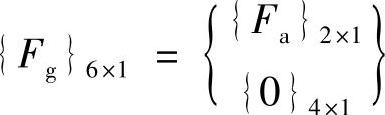，。可见，应用Craig-Bampton法，把原有的40个联立方程的求解问题缩聚为6个联立方程的求解问题。当A-集自由度选定以后（即Guy-an模态数已定），选用的固定边界模态的个数越多，计算精度越高。作为一般的准则，如果所需的最高频率为f_max，则至少应将固有频率在2f_max以内的所有固定边界模态都选进Craig-Bampton变换中去。以后，我们将A-集自由度与固定边界模态自由度合称为G-集自由度。

图4.3所示为悬臂梁右端点的加振点频率响应函数。其中，实线为利用模态法计算出的结果，点线为利用Craig-Bampton缩减法计算出的结果（采用四个固定边界模态）。两者结果几乎重叠。作为参考，虚线给出利用Guyan缩减法计算出的结果（两个A-集自由度），可见，在A-集自由度较少的情况下，Guyan缩减法的误差很大。

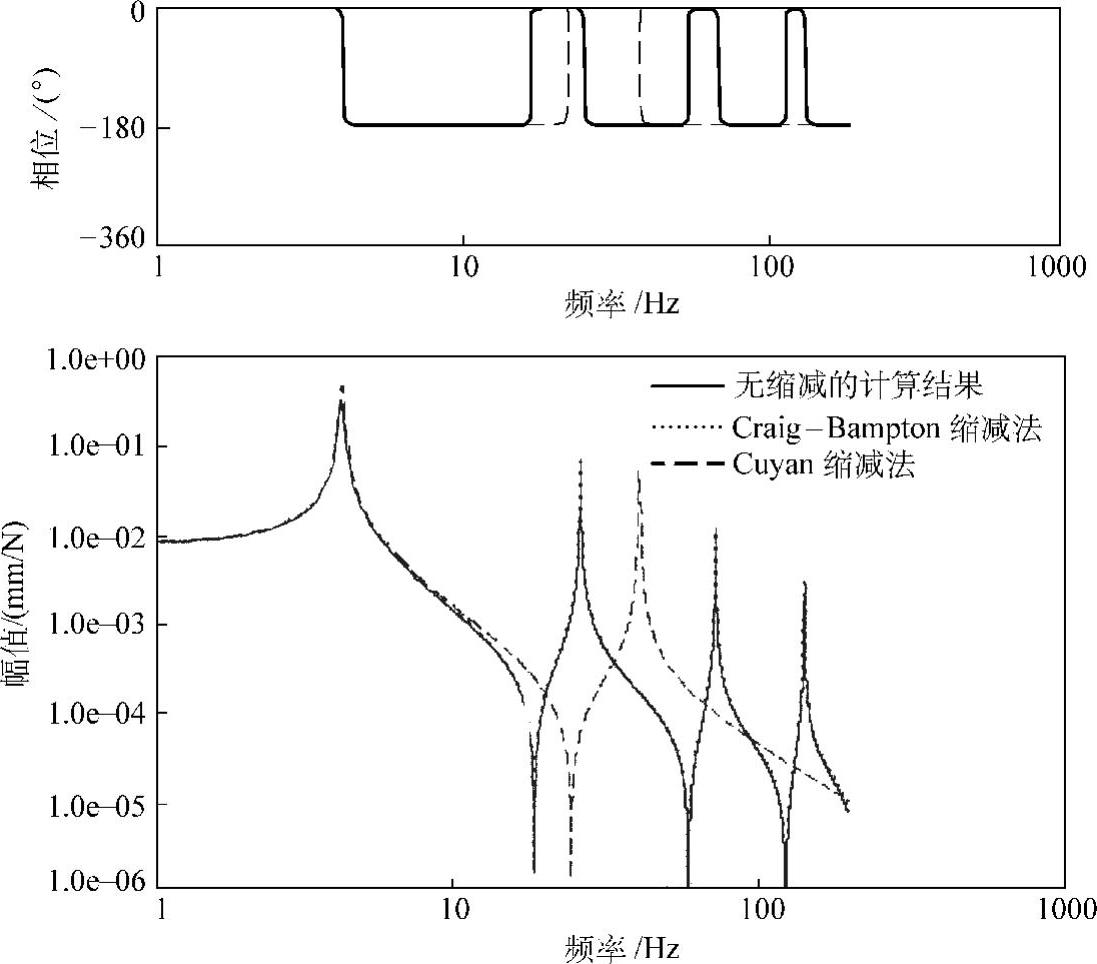
图4.3 悬臂梁右端点的加振点频率响应函数的计算结果

对于这个简单的例子来说，利用缩减法并不具有计算速度上的优势。但是，对于大规模系统来说，Craig-Bampton缩减法提供了高速求解动力学方程的计算方法的基础，这就是4.2节中要介绍的内容。