Guyan缩减方法优化建议：简单易懂的Guyan缩减技巧

有限元分析中常用的模型缩减方法是Guyan缩减法。其出发点是以下静力平衡方程

其中，{F_a}为作用在A-集自由度上的外力，{F_o}为作用在O-集自由度上的外力。式（4.6）可以写成以下两个方程

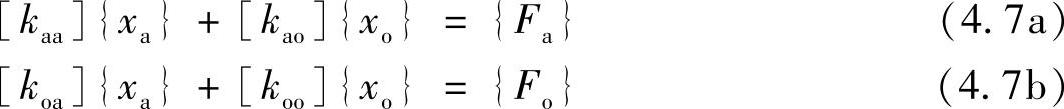
从方程式（4.7b）可以得到

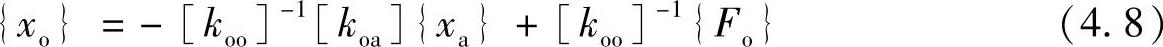
代入到方程式（4.7a）并整理，得

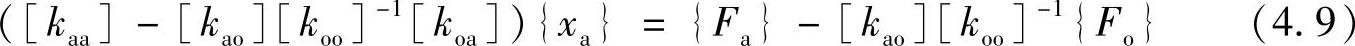
式（4.9）代表了缩减后的静力平衡方程。

为了简化说明，假定作用在O-集自由度上的外力为0（这是一个容易满足的条件，把外力不为0的点不要划分到O-集即可）。于是，式（4.8）和式（4.9）分别成为

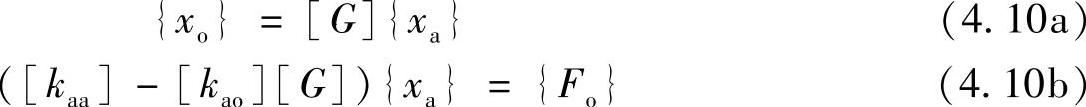
其中，[G]为（n-a）×a阶变换矩阵

[G]=-[k_oo]^-1[k_oa] （4.11）

显然，把式（4.4）定义的变换矩阵[T]中与频率变量关联的质量项略掉，即可得到这个变换矩阵。由于Guyan缩减法是建立在静力平衡方程基础之上的，因此也称为静力缩减法（Static Reduction）。

现在来看看如何把Guyan缩减法应用到以下动力学方程的求解中去。

（[k]-ω²[m]）{x}={F} （4.12）(https://www.xing528.com)

做以下变换

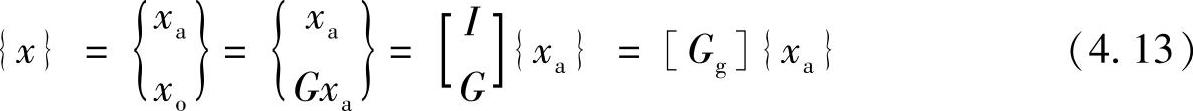
其中，[I]为（a×a）单位矩阵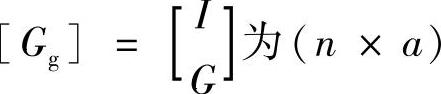，阶矩阵。将其代入到式（4.12），可得

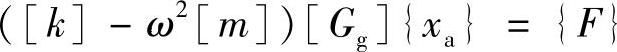
给上式两边同乘以[G_g]^T，得到缩减后的动力学方程为

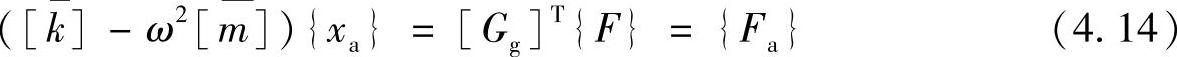
这里，缩减后的刚性矩阵与质量矩阵分别为以下（a×a）阶矩阵

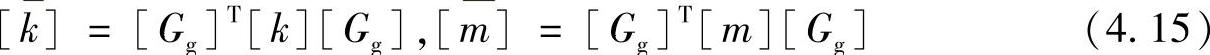
这样，就可以在压缩了的自由度上求解原有系统的特征值或响应问题，从而提高计算速度。在得到A-集自由度上的响应后，如果需要的话，可以通过式（4.10a）求得O-集自由度上的响应。这个过程叫做还原计算（Recovery）。

根据变换公式（4.10a），当{x_a}的第i个元素为1、其余元素为0时，{x_o}={G_i}，即变换矩阵[G]的第i列就是O-集自由度上的变形。也就是说，[G]的每个列对应于一个A-集自由度在其他A-集自由度被约束的情况下，强制作用一个单位变形时的O-集自由度上的变形（模态）。因此，把[G]也叫做Guyan模态矩阵。[G]的列数等于A-集自由度的个数，行数等于O-集自由度的个数。如果系统没有约束，则得到的[G]为强制刚体位移。

应该注意，Guyan缩减法中的矩阵变换对刚性矩阵来说是严格进行的，但对于质量矩阵来说，由于忽略了与O-集自由度相关的质量，这个变换是近似性的。因此，对于静力变形问题，Guyan缩减法不会影响计算精度；但对于动态问题来说，所得到的固有值或者响应是近似结果。为了减少误差，在选取A-集自由度时，应尽量把质量较大的部位包括进来。此外，Guyan缩减后的刚性矩阵变得非常稠密，对于现在广泛利用稀疏矩阵特征的算法（Sparse Solver）来说，Guyan缩减并不有利，因此对于一般规模的静力变形问题，用Guyan缩减法可能得不到太多的计算速度上的好处。

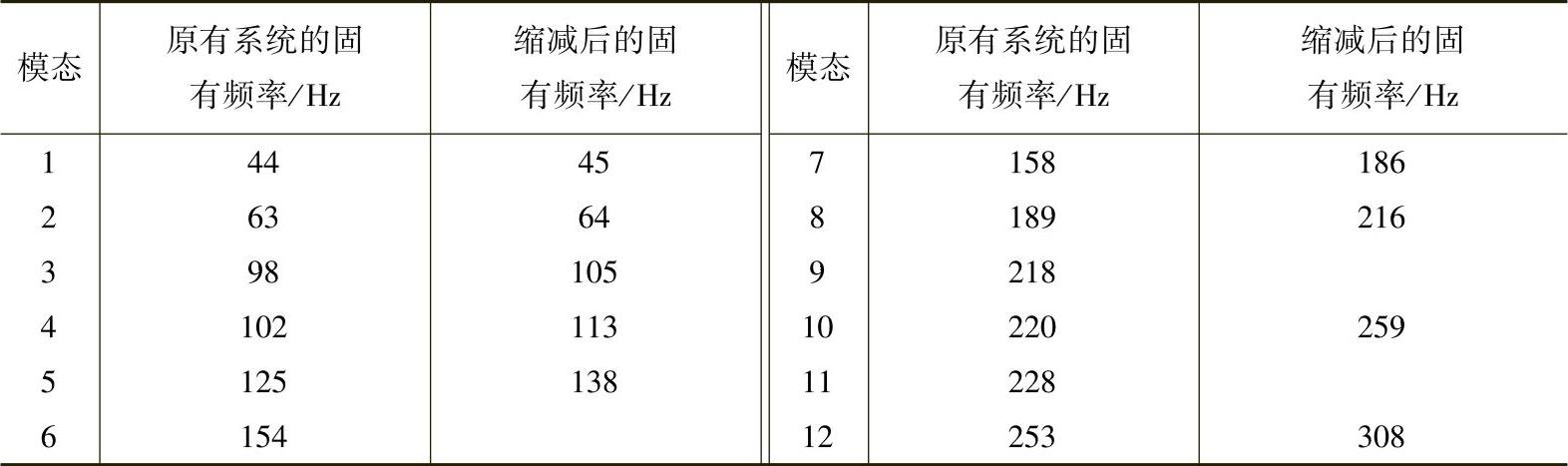
这里，作为举例，对第3章最后所介绍的平板结构（见图3.28）利用Guyan缩减法求解其固有值。该有限元模型总共有3306个自由度。选取如图3.29所示的9个模型点的面外方向的自由度为A-集自由度，则利用Guyan缩减法，可以把原有系统缩聚为9自由度系统。表4.1所示为缩减前后模态的固有频率。可见，利用Guyan缩减法计算出的固有频率偏高，并且频率越高，误差越大。这是由于忽略掉部分质量而引起的。另外，原有系统的第6阶、第9阶和第11阶模态在缩减后的系统中不存在，这是由于选取的9个自由度反映不了这些模态的缘故。所以，在应用Guyan缩减法时，根据需要选择合理的A-集自由度很重要。

表4.1 图3.28所示平板结构的缩减前后模态的固有频率