集中参数模型的状态反馈控制与建模方法

上节介绍了对多自由度系统实施模态控制的方法。尽管反馈控制设计是在模态坐标上进行的，其实还有赖于物理坐标上的测量与激振。因此，需要利用模态矩阵将物理坐标上的响应转换为模态状态向量，还需将模态控制力转换成实际的执行器的驱动力。如果传感器数目不够多，则估算出的模态状态量可能误差较大。此外，虽然利用模态截止方法可以大大降低模态自由度数（p<<n），参与上述变换的模态向量的长度依然为n，运算负担仍可能较大。

本节介绍一种在物理坐标上实施控制设计的建模方法。其步骤是：利用已经得到的原有系统的模态参数（可由实验方法或数值方法得到），经过逆运算建立可以代表所要控制的p个低阶模态的动态特性的离散模型。这个低阶模型的自由度数为p，并且由物理坐标上的集中参数构成（质量，弹簧），因此，可以直接方便地进行最优控制设计。之所以用少数自由度的集中参数模型可以代表原有的较大自由度数的系统的动特性，还是基于模态控制的思想，即只要模态变形上的一点或数点的特性得到了较好的模型化，并对这些点实施控制，则整个模态变形会得到抑制。

以悬臂梁为例，图3.15所示的模态变形是由有限元分析得到的。整个悬臂梁划分为20个梁元素，共有21个节点。除了左端点被完全约束外，其余节点在XY平面内具有2个自由度（Y方向上的平移和绕Z方向的旋转），总共有40个自由度。也就是说，图3.15所示的模态变形是由这40个自由度表现的。从模态控制的角度来说，只要把每个模态的特征表现出来即可，因此，可以设想用4个质点的运动来代表4个模态，如图3.25所示。这4个质点只有Y方向上的平移自由度，因而这个集中参数模型只有4个自由度。选取4个质点是为了表现第4阶模态的变形特征。如果只要表现第1阶模态，则1个质点即可（如m₄）；同样，如果还要表现第2阶模态，则需2个质点（如m₂、m₄）；表现第3阶模态，则需3个质点（如m₁、m₃、m₄）。总之，这里选取的4个质点可以同时表现从第1阶模态到第4阶模态的特征。给这4个质点赋予适当的质量，并把各质点通过弹簧接地，同时把各个质点通过弹簧相连接，则可以构成如图3.26所示的集中参数模型。现在的问题是如何决定这些质量和弹簧的值。

根据3.3.3节介绍的模态向量的正交性质，对于质量正规化后的模态形状矩阵来说，具有以下性质

其中，[I]为单位矩阵，[Ω]为对角矩阵，其对角元素为各个模态固有角频率的平方。对式（3.92）进行逆运算，可得质量矩阵和刚性矩阵为

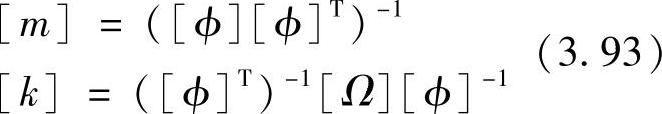
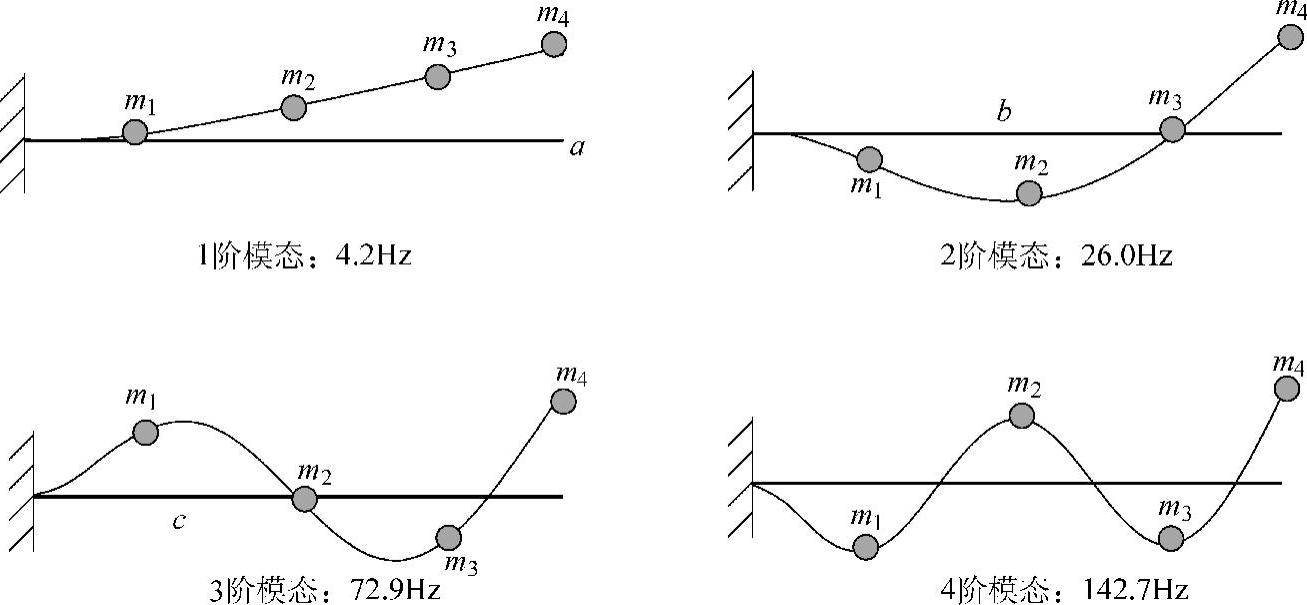
图3.25 用4个质点来表现悬臂梁的4个模态的变形特征

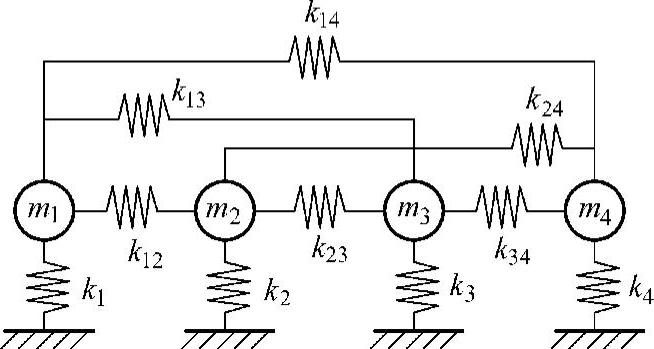
图3.26 悬臂梁的四自由度集中参数模型

对于图3.26所示的系统来说，如果知道了该系统的质量正规化后的模态形状矩阵及模态频率，用式（3.93）即可求得模型中的各个参数（质量和弹簧常数）。由于建立的这个集中参数模型是为了表现原有系统的前4阶模态的动特性，合适的做法就是由原有系统的前4阶模态在各个质点位置的模态变形，来构成这个新建立的集中参数模型的模态变形矩阵。这相当于对原有系统的模态向量在各个模型点进行空间采样，从而形成新的缩小了的模态向量。具体到这里的悬臂梁结构，可以构成以下模态矩阵（原有系统的模态向量由有限元分析得到，结果略去）

计算[ϕ][ϕ]^T，可得

可见，[ϕ][ϕ]^T对称但并不是对角矩阵。其理由是：尽管原有系统的模态向量具有正交性，但并不能保证通过对其采样得来的缩小了的[ϕ]也是正交的，因此，[ϕ][ϕ]^T的非对角元素不为零。也就是说，用以上方法构建的[ϕ]并不是图3.26所示模型的真正的模态形状矩阵，而只是一个初始值。我们可以以这个初始值为起点，通过以下步骤对[ϕ]进行修正，以使它满足正交性。

由矩阵乘法运算可知，[ϕ][ϕ]^T的非对角元素（这里有6个元素）可以写成以下6个关系式

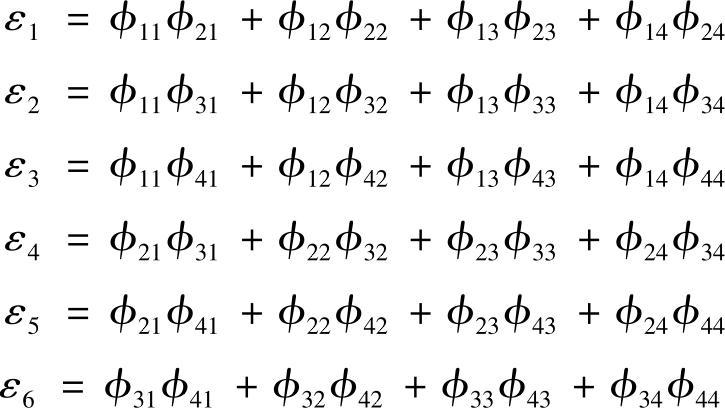
其中，含有16个模态变形成分。由这些模态变形成分构成以下向量

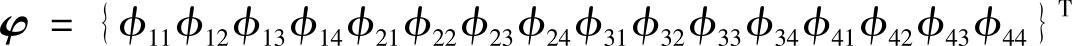
并定义一个残差向量

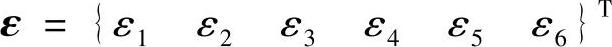
显然，ε是φ的函数，ε=f（φ）。

我们的目的是通过修改φ，以设法使ε变为零，即寻找φ的增分δφ，使残差从ε变为0。用公式表示为

这里，ε对φ的偏微分矩阵定义如下

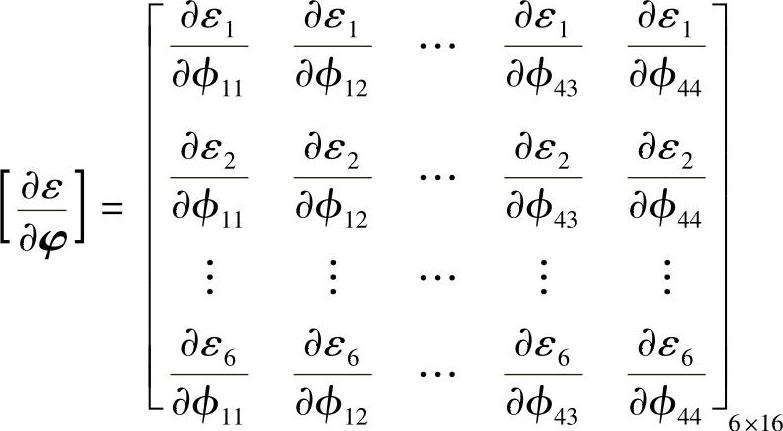
由式（3.93）可得，增分向量δφ为

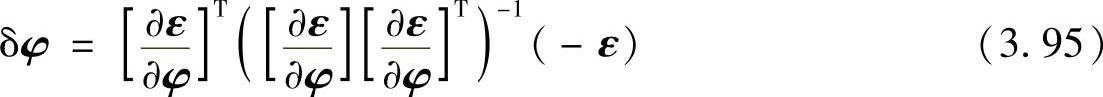
新的向量为

φ+δφ⇒φ

以上过程经过若干次反复运算，可以使ε趋于0。这里经过5次反复，得到最终的四自由度模型的模态形状矩阵为

验算[ϕ][ϕ]^T，

可知，其为对角矩阵。

于是根据式（3.93），可以求得该模型的质量矩阵为(www.xing528.com)

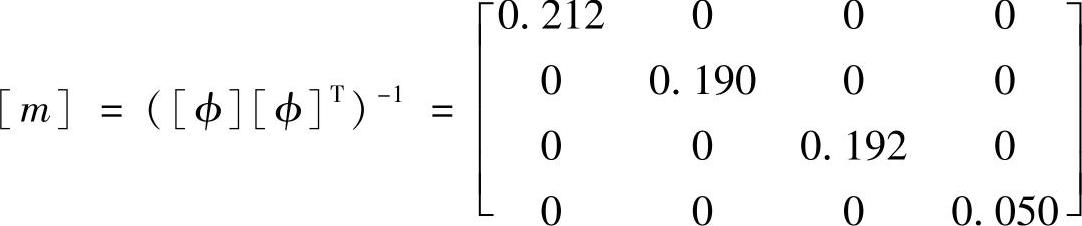
对角线上的元素分别是各个模型点的等价质量。刚性矩阵为

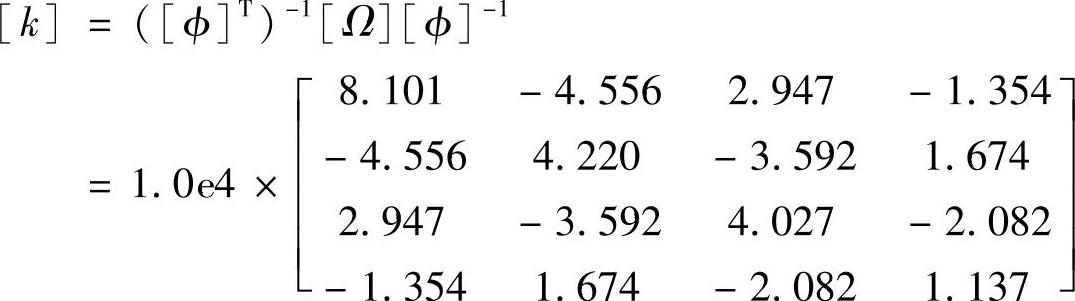
进一步可以得到图3.26中的各个弹簧常数为（单位：N/m）

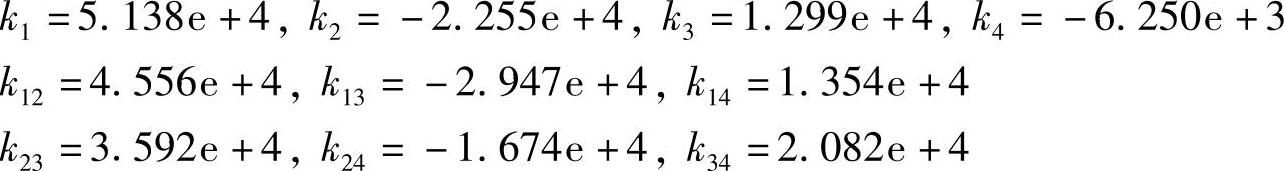
注意：有些弹簧常数为负值。这是由对原有系统的模态形状进行修改而引起的，其作用就是为了使得建立的低阶集中参数模型的动特性接近于原有系统的特征。由于建立起来的模型是纯粹的数学模型，不存在如何实现的问题，所以负的弹簧常数是允许的。

以上就是建立集中参数模型的方法。这样建立的模型并不是简单地对原有系统进行模态截止得来的，而是一个新的在物理坐标上描述的低阶模型，因而可以方便地应用LQ最优控制理论进行状态反馈控制设计，从而避免了3.8.2节介绍的模态控制设计的坐标转换的问题。

图3.27所示为建立的悬臂梁的四自由度模型的频率响应函数与原有系统的频率响应函数的比较。二者都是在右端点（模型质点4的位置）进行激励并检测该点的响应得来的，计算中都用了0.1%的阻尼比。可见二者特性基本吻合，表明建立的四自由度低阶模型可以反映出原有系统的前4阶模态的动特性。检测其他模型点的传递频率响应函数，可以得到同样良好的结果。

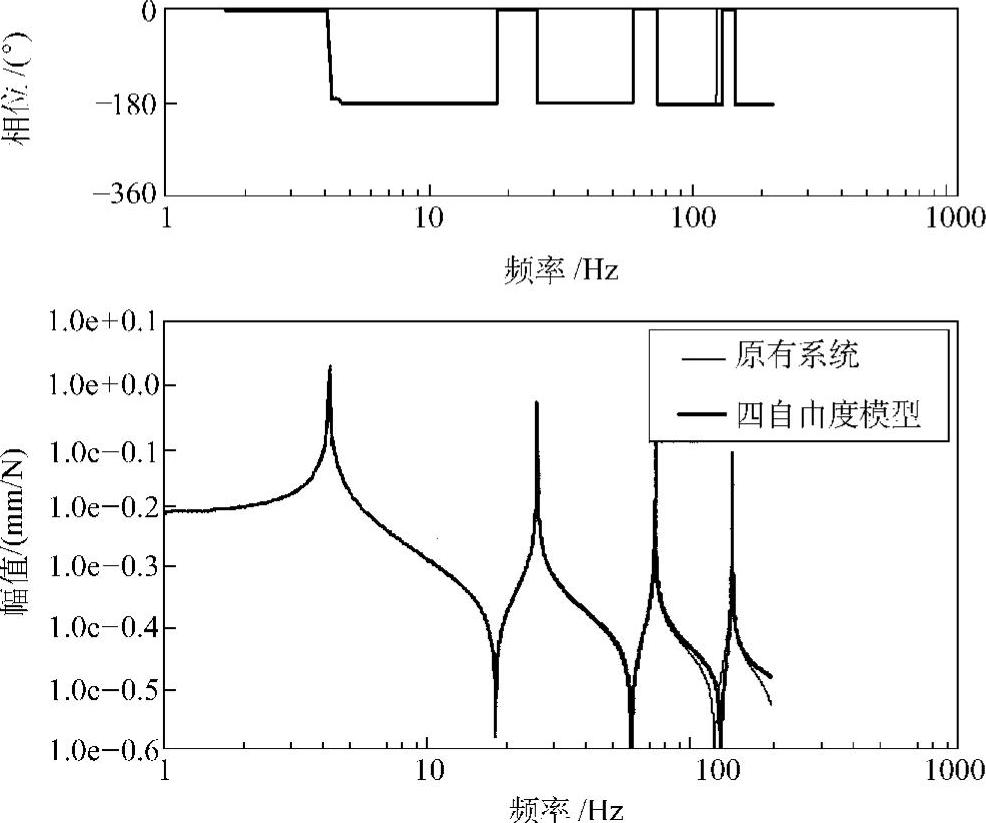
图3.27 悬臂梁的四自由度模型的频率响应函数与原有系统的频率响应函数的比较

表3.2给出以上模型化的Matlab计算程序。

表3.2 建立集中参数模型的Matlab程序

（续）

作为该方法的应用举例，这里介绍对周边固定的平板结构进行振动噪声控制的实验结果。

研究对象是一个400mm×600mm×1.2mm的钢板，用上、下两个钢框架将其周边固定。图3.28所示为有限元分析得到的这个平板结构的前12阶模态。经过分析，决定对其中的声辐射效率较高的1阶、3阶、8阶、11阶和12阶的5个模态进行控制。根据这些模态的特点，选取9个模型点（见图3.29），运用上面介绍的建模方法建立起九自由度的集中参数模型，如图3.30所示。9个集中质量与45个弹簧常数的具体值略去。由于这些模型点的位置正好处于第6阶和第9阶模态的节线（变形为0的线）上，因此这两个模态无法表现。此外，如果选取控制力作用点位置在平板中央位置，则第2阶、第4阶、第5阶、第7阶和第10阶模态得不到控制。这样，就可以把对象模态以外的7个模态排除在外，同时利用这些模态的不可观测和不可控性，保证了在这些非控模态上不会发生“溢出”现象。

根据以上建立的九自由度集中参数模型（见图3.30），进行LQ反馈控制设计，并利用第2章介绍的准最优控制的方法，可以确立利用3个传感器和1个执行器的控制系统。在这个研究中，传感器采用非接触的涡电流传感器（Gap Sensor），这样可以直接测到振动位移，经过微分回路可以得到速度。执行器为自制的电磁激

图3.28 对象平板结构的前12阶模态

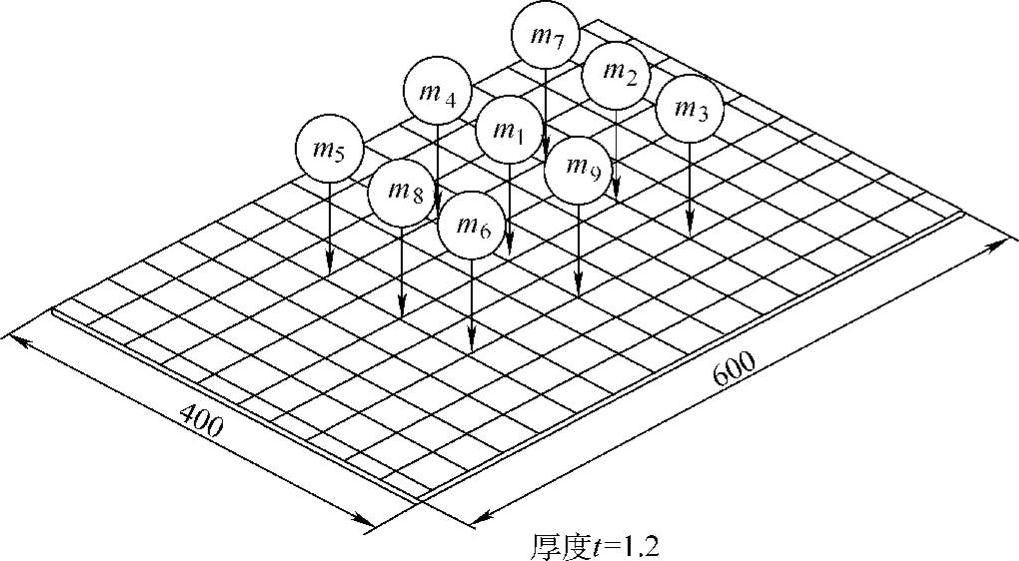
图3.29 模型点的位置

振器（Electromagnetic Actuator），如图3.31所示。图3.32为实验装置示意图。

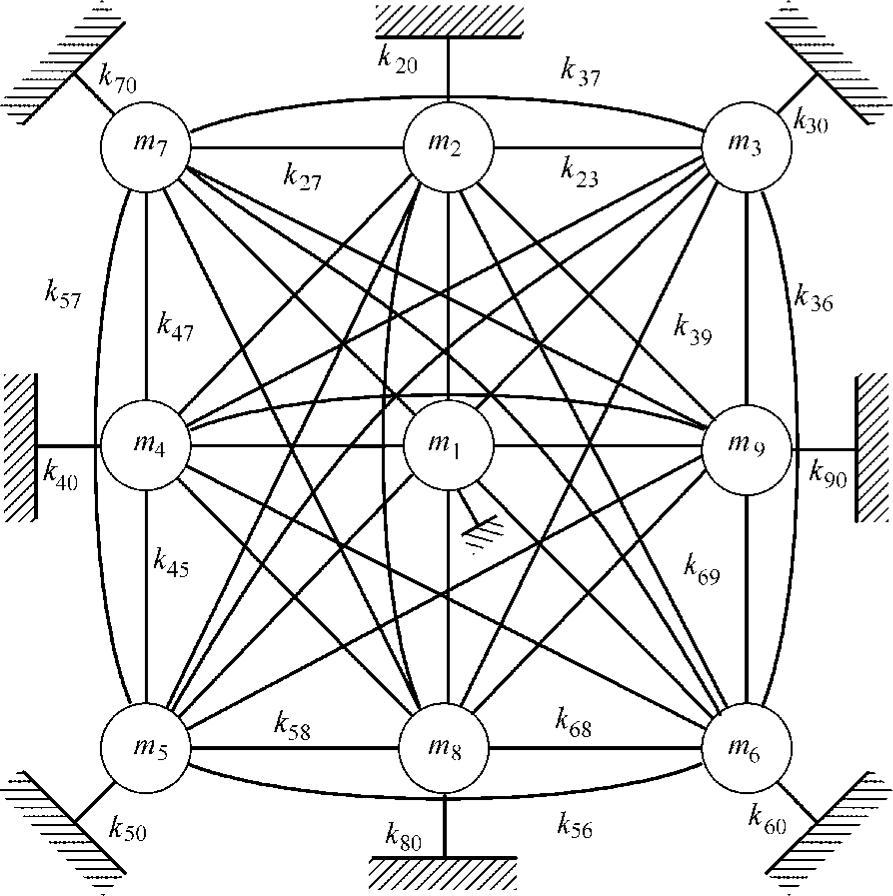
图3.30 建立的九自由度集中参数模型

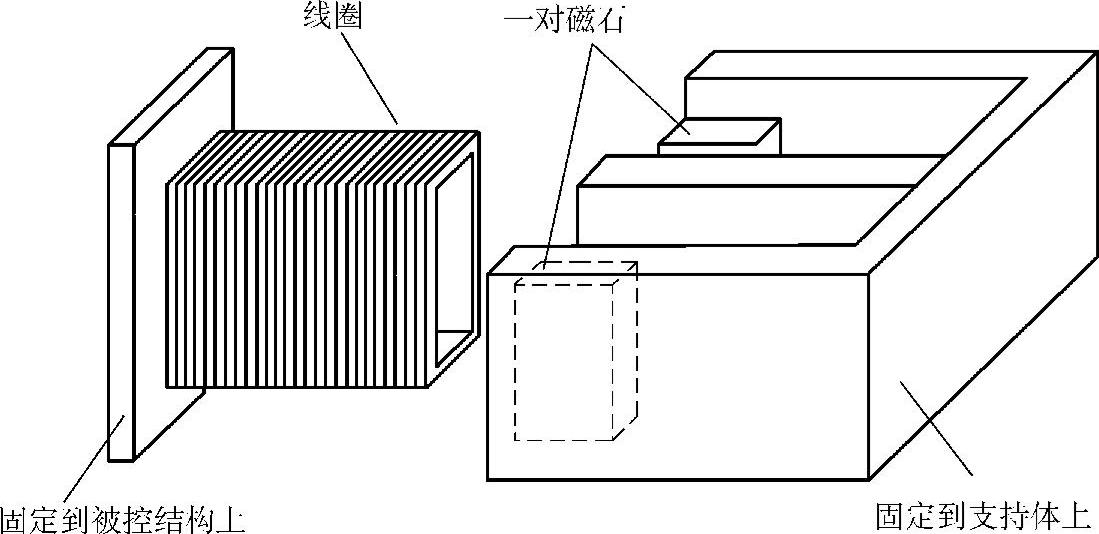
图3.31 电磁式激振器的结构

在实施控制实验之前，先利用Matlab进行仿真，得到状态反馈增益，再把这个增益用到实际的控制回路中去。在实验中，检测到的状态量（位移和速度）经过模数转换器（A/D）输入到信号处理器（DSP）中进行运算，得到的控制力信号经过数模转换器（D/A）输出到执行器去实施控制。图3.33是振动控制结果的一个例子。其中，图3.33a为在质点2用激振锤激振，在质点1附近测量响应得到的频率响应函数；图3.33b为在质点1激振，在质点1附近测量响应得到的频率响应函数。可见，振动峰值得到了良好的控制。在其他非模型点位置测量，也有同样良好的控制效果。

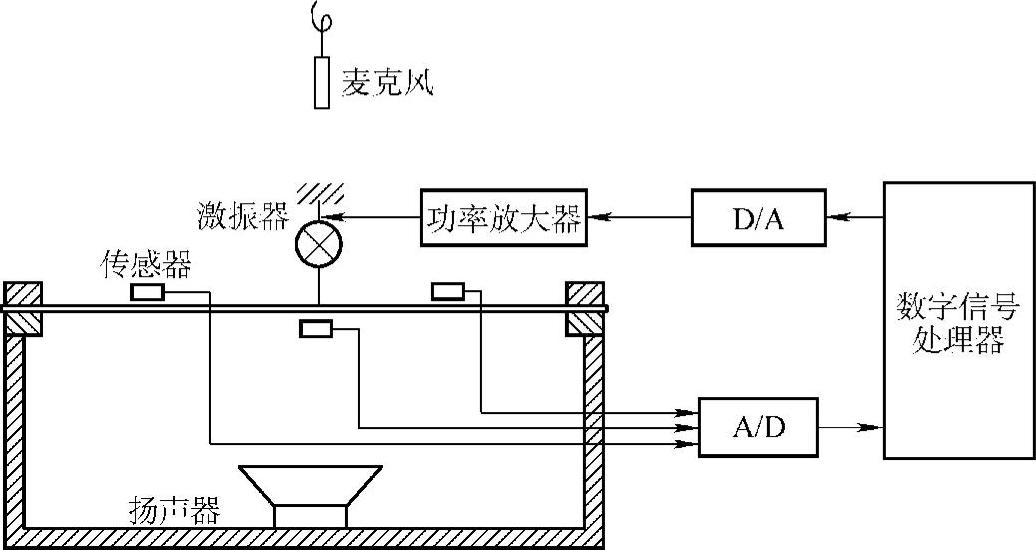
图3.32 实验装置示意图

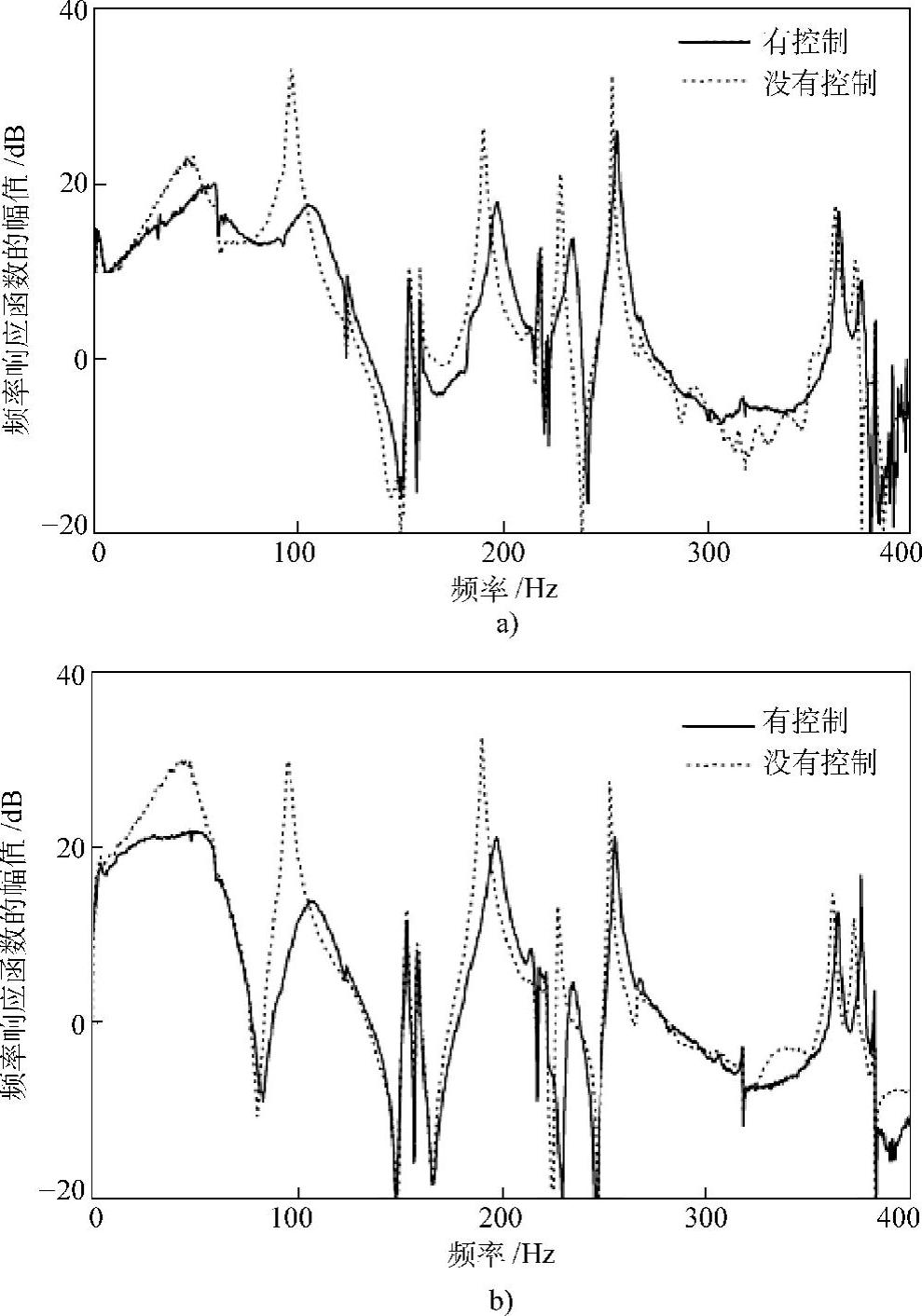
图3.33 振动控制结果

a）在质点2激振在质点1测振 b）在质点1激振并测振

另外，利用扬声器的0～400Hz的白噪声信号进行声响激励，并在平板上方0.5m的位置测量声压频谱，结果如图3.34所示。平板的声辐射也得到了良好的控制。

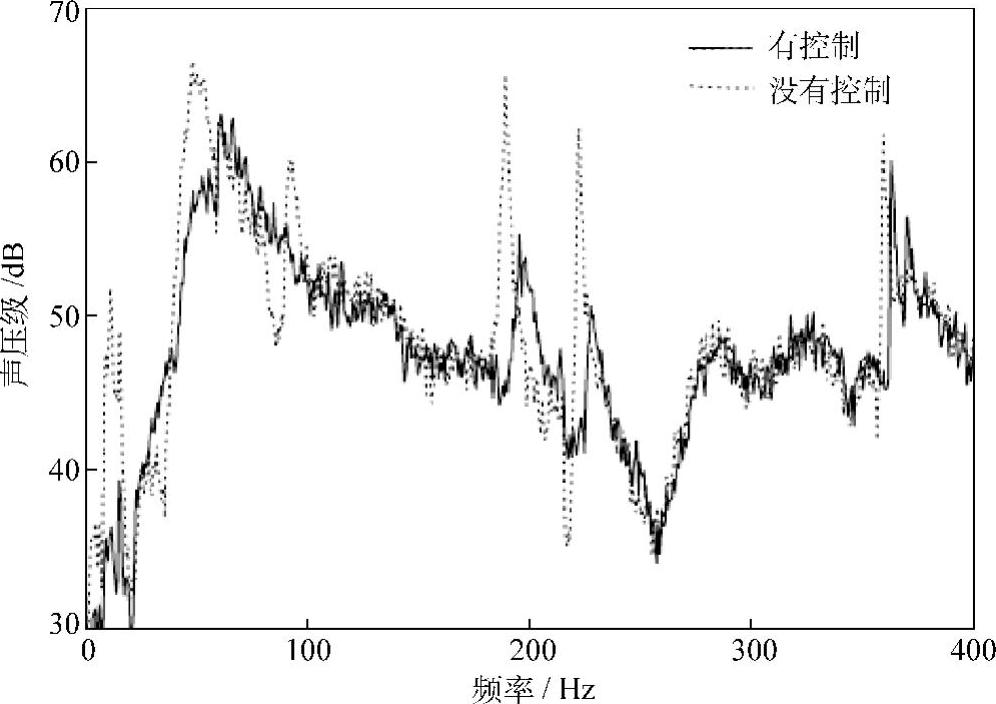
图3.34 扬声器激励下的噪声频谱