动力吸振器在机械领域的应用

在第2章中，我们针对单自由度系统介绍了动力吸振器的最优设计原则。这里来介绍对于实际的结构如何运用这种设计方法。图3.14所示为一个长方形断面的钢质悬臂梁结构，总质量为0.78kg。假定该悬臂梁只能在XY平面中振动，利用有限元分析，可以得到它的前4阶模态，如图3.15所示。此外，图3.16为在悬臂梁右端点加振时观测到的该点的频率响应函数（模态阻尼取为0.1%）。现在来考虑利用动力吸振器来控制该结构的振动。

图3.15 悬臂梁结构的前4阶模态

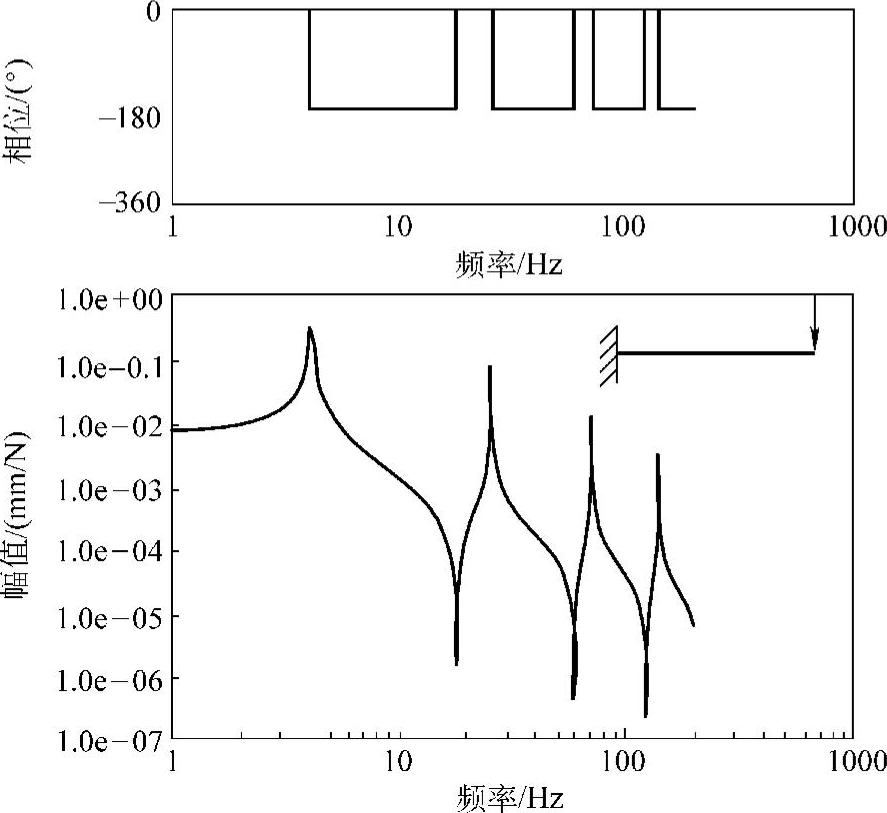
图3.16 悬臂梁结构的频率响应函数（驱动点柔顺性函数）

首先考虑控制第1阶模态。由图3.15所示的模态形状可知，悬臂梁最右端a点的模态变形最大，具体来说，质量正规化后的模态向量在该点的绝对值最大，为2.262。由式（3.36）可得，该点的等价质量为

这是第1阶模态中等价质量为最小的点。在这点上安装动力吸振器所需的附加质量也最小，因此效果最好。取质量比μ=0.1，则吸振器的质量为

m₁=μM^eq₁=0.0195kg

根据第2章中介绍的动力吸振器最优设计原则，同调频率为

ω₁=Ω_n1/（1+μ）=（2π×4.2/1.1）Hz=23.99Hz

于是，吸振器的支持刚性为

k₁=m₁ω²₁=（0.0195×23.99²）N/m=11.223N/m

再根据最优阻尼的式（2.33），可以得到吸振器的阻尼为

这样，就确定了动力吸振器的各个参数（质量、刚性、阻尼）。把这个动力吸振器安装在a点（如图3.17所示），再计算该点的频率响应函数，可得如图3.18所示的结果。可见，第1阶模态频率处的峰值得到了良好的控制。

然后，考虑控制第2阶模态。由于在a点已经设置了一个吸振器，控制第2阶模态的吸振器显然应设置在b点。假定激励力在a点，则第2阶模态在b点的等价质量为

其中，ϕ_a2=2.261为第2阶模态在激励点a的模态变形，ϕ_b2=-1.621为第2阶模态在响应点b的模态变形。同样取质量比μ=0.1，则可以确定该动力吸振器的最优参数为

m₂=0.0273kg

k₂=602.12N/m

c₂=1.497N·s/m

图3.19所示为同时在b点安装上以上吸振器后，在a点观测到的柔顺性函数。可见，第1阶和第2阶模态频率处的峰值同时得到了良好的控制。

图3.17 控制悬臂梁结构第1阶模态的动力吸振器

最后，考虑控制第3阶模态。控制该模态的吸振器显然应设置在c点。假定激励力在a点，则第3阶模态在c点的等价质量为

同样取质量比μ=0.1，则可以确定该动力吸振器的最优参数为(www.xing528.com)

m₃=0.0257kg

k₃=4490.86N/m

c₃=3.983N·s/m

在a点安装上控制第1阶模态的动力吸振器，在b点安装上控制第2阶模态的动力吸振器，同时在c点安装上控制第3阶模态的吸振器后，图3.20所示为在a点观测到的柔顺性函数。可见，第1、2、3阶模态频率处的峰值同时得到了良好的控制，甚至第4阶模态频率处的峰值也得到了一定程度的抑制。

图3.18 悬臂梁结构第1阶模态的控制效果（驱动点柔顺性函数）

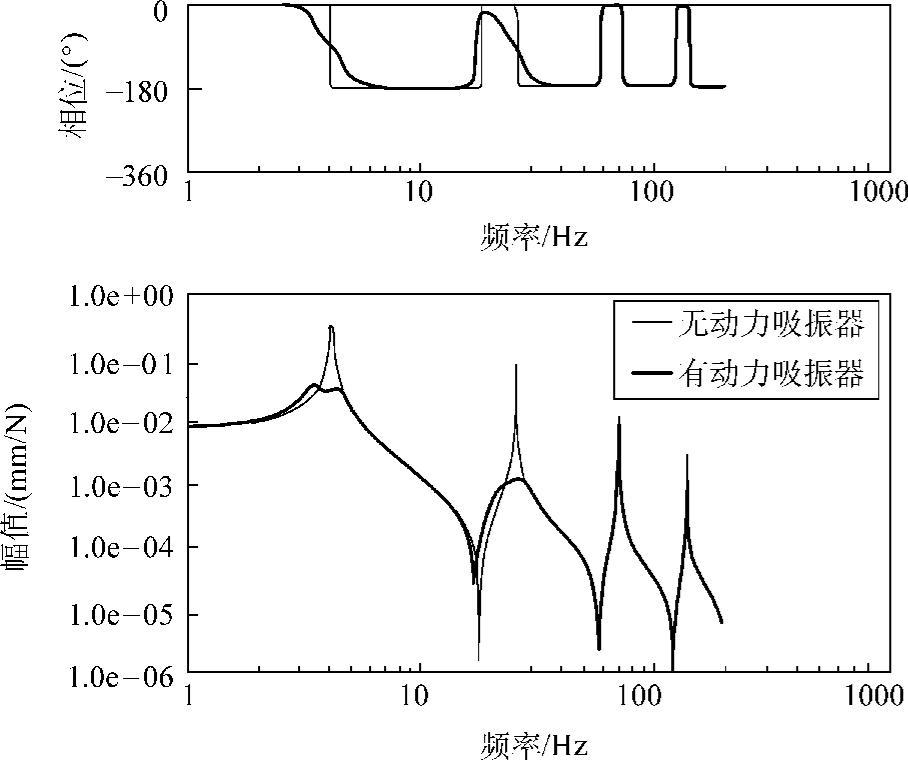
图3.19 悬臂梁结构第1阶及2阶模态的控制效果（驱动点柔顺性函数）

图3.21所示为在a点激振、在b点观测到的传递柔顺性函数，同样，对象模态频率处的峰值得到了良好的控制。图3.22所示为在a点激振、在b点观测到的瞬态响应函数。可见，附加了3个动力吸振器后，振动响应得到了快速衰减。

三个吸振器的质量总和为0.072kg，相当于悬臂梁质量的1/10以下。可见，这是一种有效的给原有结构附加阻尼的振动控制方法。总而言之，基于单自由度系统的动力吸振器的设计理论可以方便地应用到实际结构的振动控制中去。其基本思想就是把结构的各个模态当作单自由度系统来对待，对目标模态进行控制。这里，关键的步骤是确定吸振器设置位置的等价质量。如果利用有限元分析或者实验模态分析方法得到了结构的模态参数，则利用式（3.36）就可以方便地得到设置点的等价质量。在上面的例子中，考虑上了激励力的位置。在激励力位置未知的情况下，可以简单地认为等价质量为M^eq_i=1/ϕ²_i，其中，ϕ_i表示第i阶模态在设置位置的经过质量正规化后的模态向量的值。设动力吸振器的质量为m，则质量比为μ=m/M^eq_i=mϕ²_i，最优同调频率比（吸振器的固有频率与结构的第i阶模态频率之比）和最优阻尼比分别为

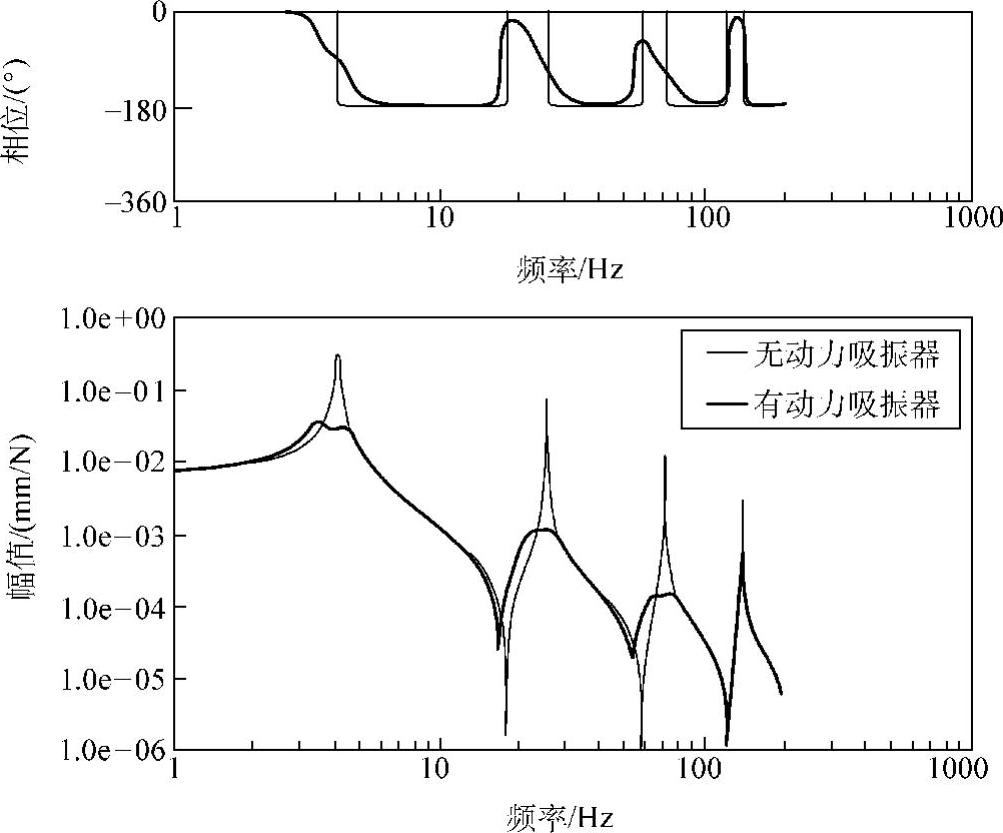
图3.20 悬臂梁结构前3阶模态的控制效果（驱动点柔顺性函数）

图3.21 悬臂梁结构前3阶模态的控制效果（传递柔顺性函数）

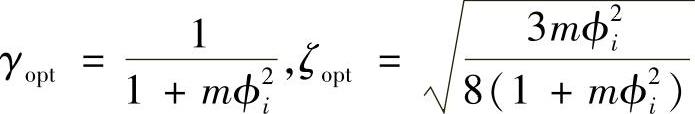
据此可以确定控制第i阶模态的动力吸振器的刚性和阻尼系数的值。

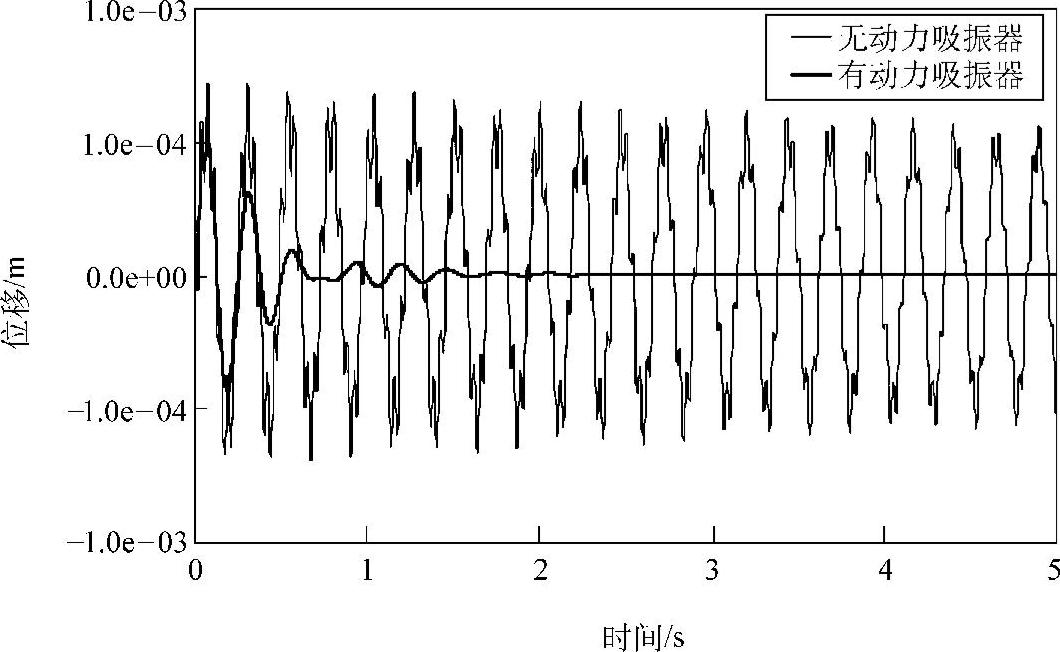
图3.22 悬臂梁结构的自由振动控制效果（瞬态响应函数）

当没有条件进行模态分析时，可以利用以下简易方法确定吸振器设置位置的等价质量。首先测量结构的频率响应函数，以确定需要控制的峰值频率。设该目标频率为Ω₁，则有以下关系

其中，M可以理解为设置位置的等价质量，K为等价刚性。然后在设置位置附加一个小质量Δm，再次测量该点的频率响应函数，目标频率会有一个小的变动，成为Ω₂，其公式为

由式（3.78）和式（3.79）可得，等价质量为

这个简易方法很实用，称为质量感应法。使用该方法应注意的问题是附加质量不能太大，以免改变原有结构的振动模态。但是如果附加质量太小，则目标频率的变化不明显，在测量仪器分辨率不够高时，易引入测量误差。为了提高精度，可以附加几种不同大小的质量，得到相应个数的等价质量估计值，然后对得到的等价质量与附加质量进行最小二乘相关分析。根据得到的线性关系，推出附加质量为0时的等价质量，就是所要的结果。这样可以尽量排除掉附加质量带来的影响。

另外一种方法就是测量设置位置的惯量函数（加速度与激励力之比），在模态分离得很开的情况下，有可能直接从频率响应曲线的质量线上（massline）估测出该点的等价质量。