模态有效质量的重要性和优化策略

由3.7.2小节可知，在强制运动激励下结构的振动由下式决定

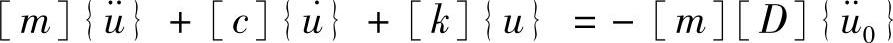
如果考虑一个方向上的运动，如r方向，上式变为

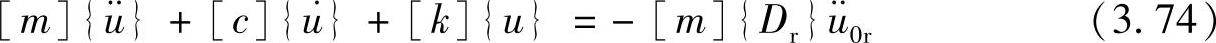
这是一组微分方程，其中，{D_r}是一个（n×1）向量。给式（3.74）两边同乘以{D_r}^T，得

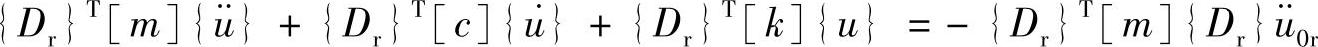
上式是一个单个的微分方程，反映了结构在r方向上的响应。这里定义

这个量的量纲为质量，反映了从r运动方向上观察到的结构的质量。下面，我们从另外一个角度来考察这个量。

回到式（3.74），利用模态坐标变换式（3.22）把它转换到模态坐标，并给两边同乘以[ϕ]^T，得到模态参数表示的模态方程

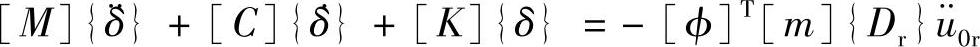
上式右边为一个向量，表示由于r方向的强制运动产生的作用在各个模态上的等效动载荷。从这个角度，可以定义一个模态贡献因子（Participation Factor）

{p}=[ϕ]^T[m]{D_r} （3.76）

由于模态向量为正交向量，任何运动均可由它们的线性组合得到。因此，刚体运动向量{D_r}可以写为(www.xing528.com)

{D_r}=[ϕ]{γ} （3.77）

这里，{γ}为一组加权系数。代入式（3.76），得

{p}=[ϕ]^T[m][ϕ]{γ}=[M]{γ}

通常，对模态形状进行质量正规化处理，由此得到的模态质量矩阵为单位矩阵，因此有{p}={γ}，或者p_i=γ_i。

另一方面，把关系式（3.77）代入式（3.75），得

m_ef={γ}^T[ϕ]^T[m][ϕ]{γ}={γ}^T[M]{γ}=∑γ²_i

可见，在r方向上呈现的等效刚体质量是各个模态贡献的总和。每一个模态的贡献称为模态有效质量（Modal Effective Mass），即

m_mef=Miγ²_i=γ²_i=p²_i

模态有效质量为模态贡献因子的平方。模态有效质量大，表示由强制运动产生的作用在该模态上的动载荷大，相应地，该模态的响应就可能大。把所有模态在各个方向上的有效质量加起来，就是结构的实际总质量。在对大规模系统应用模态法时，不可避免地要对高频模态进行取舍，计算出的模态总有效质量一般小于结构质量。如果小得太多，则说明漏掉了关键的模态。

模态有效质量是一个筛选重要模态的很有用的指标，它揭示了哪些模态支配着结构在强制运动激励下的响应。该方法不仅可以应用于土木工程中，而且可以应用在航天工程上。一般，计算出6个方向上（3个平移方向和3个回转方向）的模态有效质量，以显示在不同方向上哪些模态重要。作为举例，表3.1所示为某航天结构的模态有效质量的计算结果。在这个项目中，70Hz以下的、模态有效质量在2%以上的模态被选为目标模态。尽管模态5不满足这个准则，但由于它在T_z方向（z为平移方向）上存在较大的变形（数据略去），也被选为目标模态。

表3.1 某结构的模态有效质量的计算结果

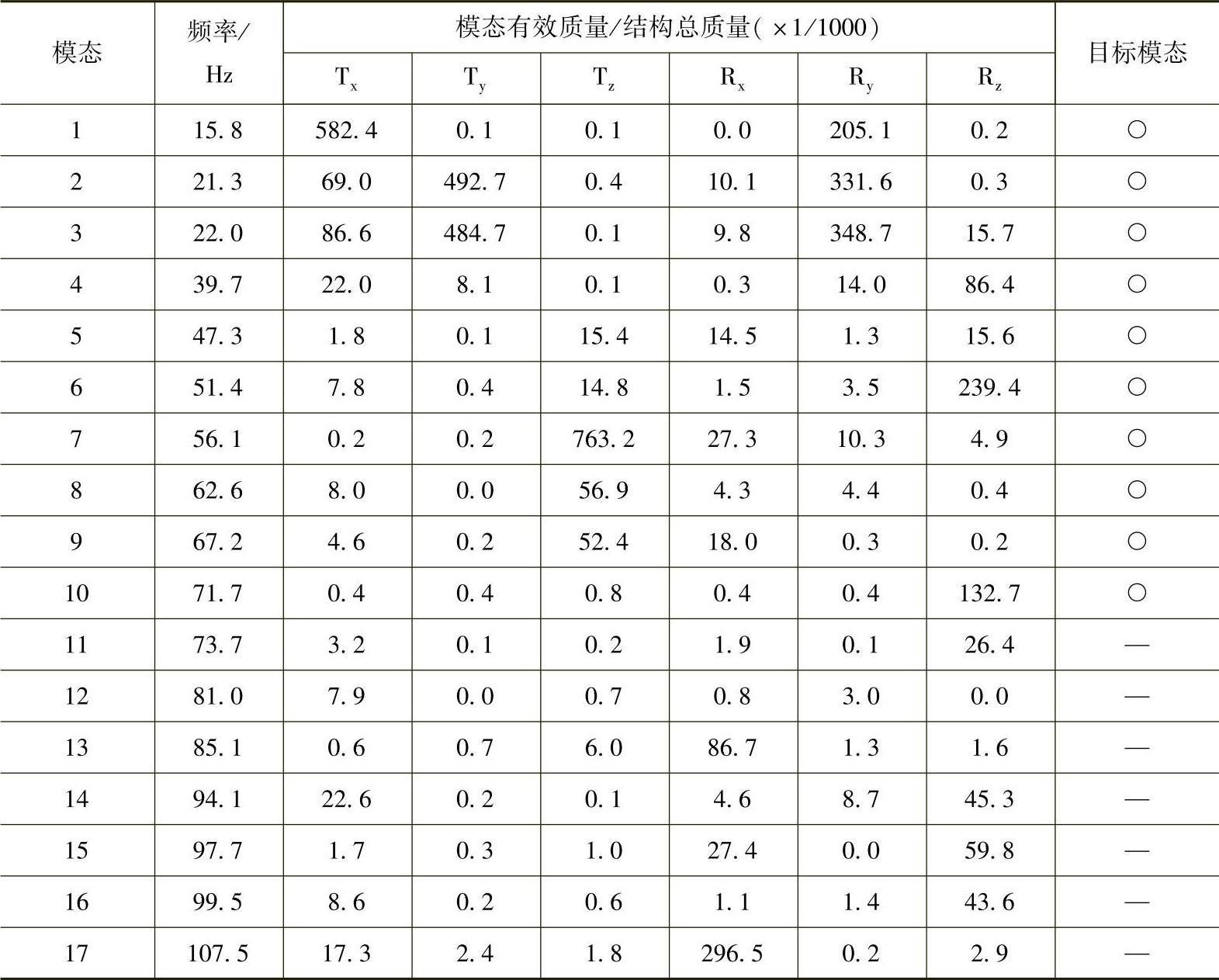
注：○表示目标模态。