最大响应估算法——冲击与响应谱分析方法

以上介绍的各种强制运动作用下的响应计算方法如果在时域求解的话，均需进行数值积分运算。这样，虽然得到的结果比较精确，但是计算成本也较大。在工程上，特别是土木工程上，常常需要对强制运动激励下结构响应的最大值做出估算，例如在地震激励下建筑物的最大变形等。这里，介绍一种较为简便的估算最大响应的方法，就是所谓的冲击与响应谱分析方法（Shock and Response Spectrum Analy-sis）。该方法是模态法时间响应分析的简化形式，其基本概念是：先计算出强制运动激励下结构各个模态的响应，然后不考虑相位关系，把各个模态的响应简单相加，从而估算出可能的最大响应振幅。该方法的优点是无需数值积分运算，计算简单高效；相应的缺点是只能得到估计值。除了估算地震激励下建筑物的振动响应外，该方法还可应用于估算飞行器内部仪器所受到的冲击响应。

首先，给出冲击与响应谱的定义。冲击谱是指一个单位质量的单自由度系统在强制运动作用下的最大响应。显然，这些最大值是在系统固有频率处得到的。对于不同阻尼，最大振幅也不同。相应地，一个单位质量的单自由度系统在力激励下的最大振幅称为响应谱。图3.12是冲击及响应谱定义的示意图。

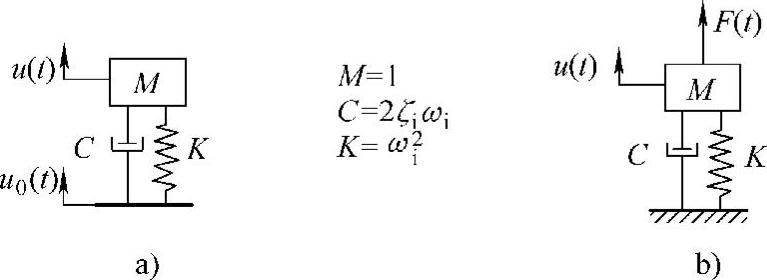
图3.12 冲击及响应谱的定义

a）强制运动作用下的冲击谱：|u|_max

b）力激励下的响应谱：|u|_max

然后，介绍该方法的原理。从式（3.65）可见，强制加速度运动所产生的等价惯性载荷为

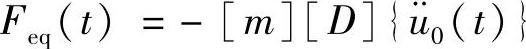
代入式（3.44），可得

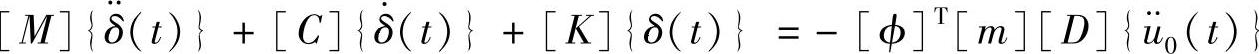
考虑比例阻尼以及模态向量经过质量正规化的情况，上式变形为

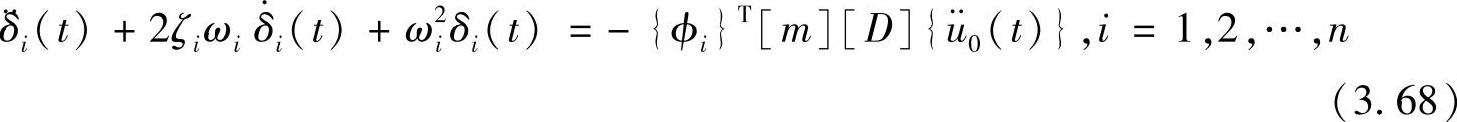
式（3.68）右边代表由强制加速度引起的作用在第i节模态上的等价模态力。这里，我们定义第i阶模态的贡献因子为{ψ_i}

{ψ_i}=-{ϕ_i}^T[m][D]

这是一个1×r向量，反映了r个方向的强制运动对第i阶模态的影响。假设强制加速度的作用点为a，且只考虑一个方向上的强制运动，式（3.68）成为

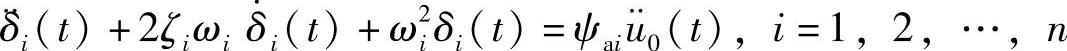
根据线性系统的叠加原理，上式的解可以写为

这里，z（ω_i，ζ_i，t）为以下单自由度系统的响应

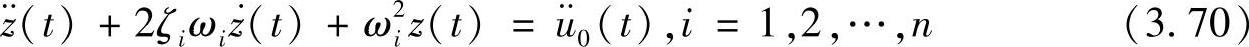(https://www.xing528.com)

把式（3.69）代入式（3.42），可以得到指定点b的实际响应为

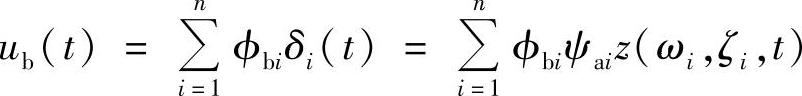
如果我们严密地求解方程式（3.70），则这个过程与前面介绍的模态法时间响应分析完全相同。这里，引入若干简化。首先，我们忽略掉方程式（3.70）的时域响应的解的细节，仅仅考虑共振时响应的最大幅值，即所谓的响应谱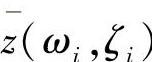=max|z（ω_i，ζ_i，t）|。其次，在模态叠加中不考虑相位关系，而取绝对值相加，得到最大可能的峰值如下

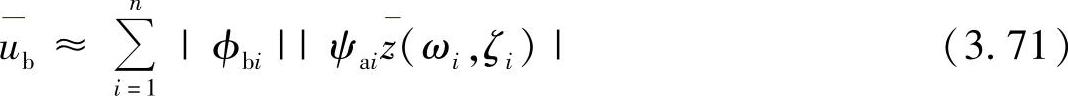
式（3.71）代表了最坏的情况，即所有模态的峰值对于结构上的每一个点来说，在同一时刻出现。显然，对于瞬间冲击，各个周期不等的模态仅有短暂的时间出现，上述这种近似误差较大；但对于延续时间较长的冲击，如地震，各个模态的峰值会反复出现，这种近似方法是可以接受的。这个近似方法称为绝对和法（ABsolute Sum method，ABS）。

一个更为现实的方法是假定模态幅值和相位按概率分布的方法相结合，得到最大响应的均方根（RMS）的估值

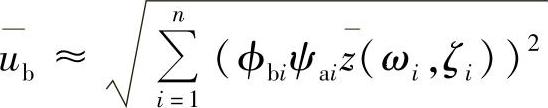
这个规则称为SRSS（Square Root of Sum-Squared）方法。这是最为常用的方法，在大多数情况下可以得到较为准确的结果。但是，这种方法假定模态响应是不相关的，每个模态的峰值在不同时间出现，因此模态耦合效应没有被考虑。这种方法得到的结果比较乐观，代表了动力响应峰值的下限。

第三种方法是ABS和SRSS的折中。它把贡献最大的第j阶模态独立出来，把其余模态的SRSS运算结果与第j阶模态的峰值响应进行绝对和运算。其关系式为

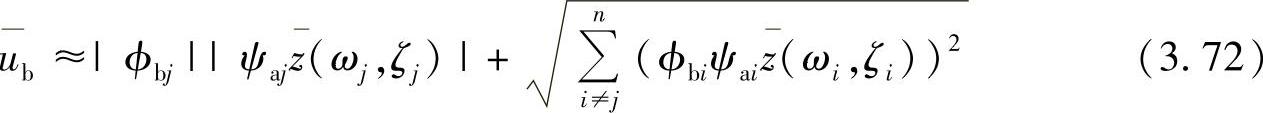
这个方法称为NRL（Naval Research Laboratory）规则。

更为复杂的运算规则是考虑上特征值密集的模态之间的耦合效果，称为CQC（Complete Quadratic Combination）方法。这种方法比前面的方法精度高，其定义为

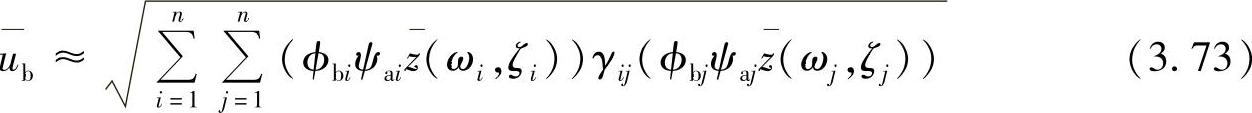
这里，γ_ij是模态i和j间的相关因子，取决于两个模态之间的模态频率之比与模态阻尼之比为

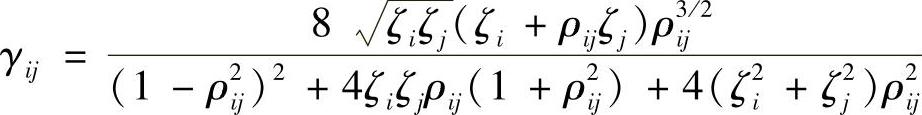
其中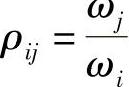，。如果模态频率分离较大，模态间的相关很小，则这个方法与SRSS的结果相同。

冲击谱分析法的关键步骤是确定响应谱z（ω_i，ζ_i）=max|z（ω_i，ζ_i，t）|。在大多数情况下，这些数据作为设计参数是已知的。如果只给出了基础结构的加速度，可以把这个强制加速度作用到一系列的单自由度振子上去，以求得它们的峰值，进而得到响应谱。对于单自由度系统来说，其共振峰值可由现成公式求得，计算很简单。每个单自由度系统的参数由结构模态分析取得，即一个模态对应于一个单自由度系统。模态阻尼可以取不同的值，以得到不同程度的响应谱，如图3.13所示。注意：只计算每个振子的振幅，它们的相位情报被忽略不计。得到响应谱后，用以上介绍的各种近似算法，即可估算出实际的物理响应幅值。

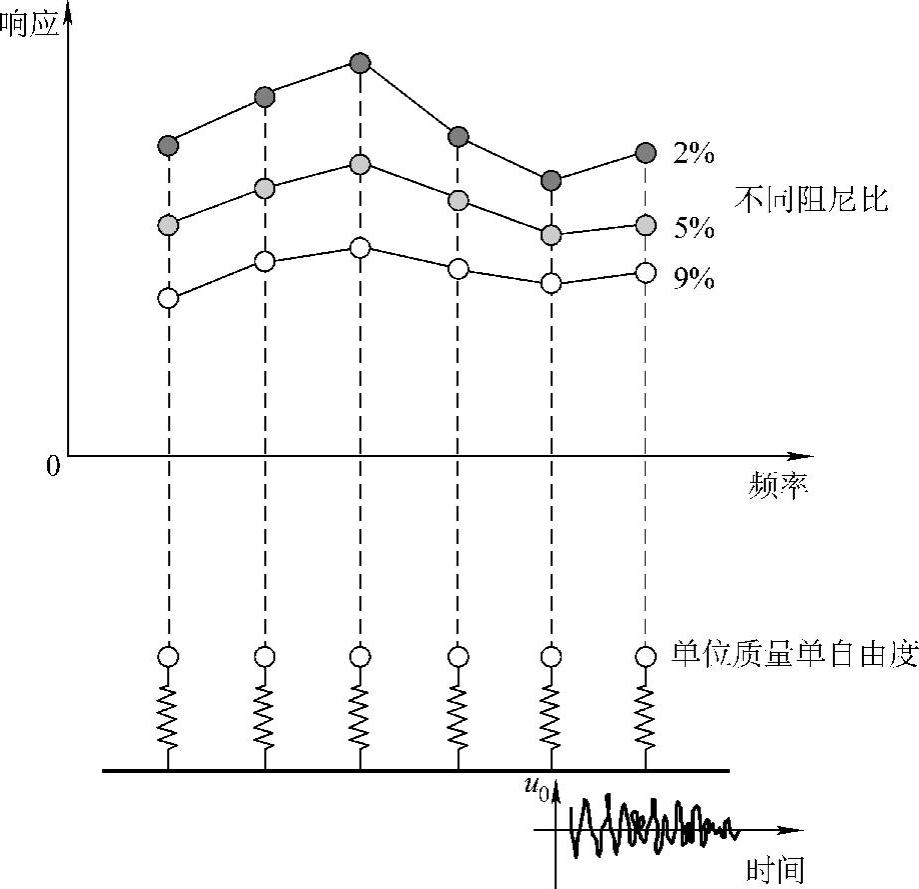
图3.13 响应谱示意图