探讨复模态和实模态的区别与联系

综上所述，在存在阻尼的一般情况下进行特征值分析，得到的特征值和特征向量一般为复数。严格地说，这些复数模态参数不同于实模态参数，但是我们可以近似地从复模态得到实模态的信息。在比例阻尼的特殊情况下（阻尼矩阵为质量矩阵和刚性矩阵的线性组合），复模态与实模态完全等价。这时，各个模态之间不存在耦合，一个模态储存与消耗的能量与其他模态无关。这种情况可以用模态坐标上的相互独立的单自由度系统来表示（如图3.8所示）。

对于实模态来说，各个点之间的相位关系是一定的（要么同相，要么反相），因此，对其放大或缩小并不改变其几何形状，即变形为零的模态的节点（线）位置不变。但是，复模态的各个点之间的相位不同，放大或缩小可能会引起模态实部与虚部之间的相对关系的变化（信息转移），使得模态节点（线）位置发生移动。因此，用不同的正规化方法可能使复模态形状发生变化。

尽管实模态只严格存在于数值分析的世界，在实际应用中，实模态的重要性却远大于复模态。复模态分析只是在某些特殊分析领域才得到应用，例如车闸的异声分析（Brake Squealing）、包含有控制系统的稳定性分析等。除非特别指明，通常所说的模态分析均指实模态分析。对于有阻尼系统，可以先略去阻尼，进行特征值分析，得到无阻尼系统的固有频率和模态形状，再将物理坐标上的联立方程转换到模态坐标上去。尽管实模态可以将质量和刚性矩阵对角化，但是一般不能同时将阻尼矩阵也对角化。因此，在模态坐标上，依然存在由模态阻尼的非对角元素而引起的模态耦合，如图3.9所示。

图3.8 比例阻尼下的物理坐标与实模态坐标(www.xing528.com)

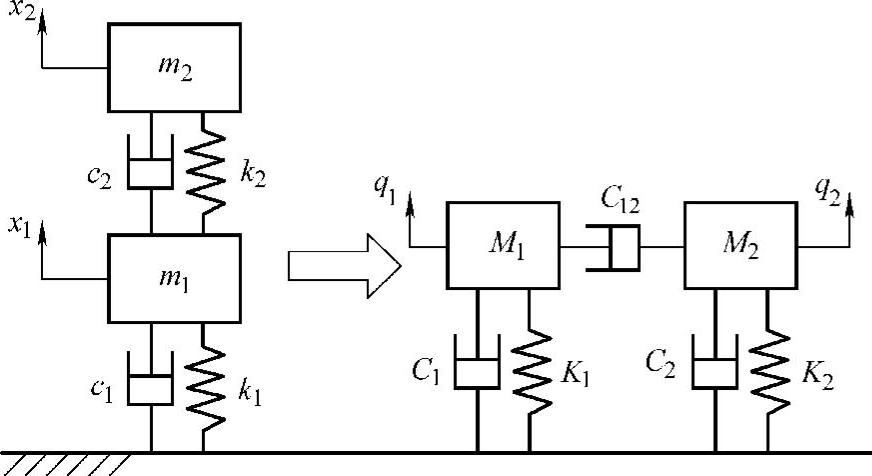
图3.9 非比例阻尼下的物理坐标与实模态坐标

需要指出，除了阻尼以外，主动控制系统、陀螺效应、空气动力效应或其他结构非线性特性（如摩擦）等原因也会导致非对称矩阵，产生复模态。