采用模态法进行瞬态时间响应分析

同模态法频率响应分析一样，模态法瞬态时间响应分析是把物理坐标上的联立方程转换到模态坐标上去，以进行数值积分运算的方法。用[ϕ]代表通过特征值分析得到的模态形状矩阵，则可以进行以下坐标变换

{x（t）}=[ϕ]{δ（t）} （3.42）

其中，{δ（t）}表示模态坐标上的响应。将式（3.42）代入式（3.6），得

给式（3.43）两边同乘以[ϕ]^T整理，得到模态坐标下的方程为

其中，[M]、[C]和[K]分别为模态质量矩阵、模态阻尼矩阵及模态刚性矩阵，{F^m（t）}是模态力向量。

在比例阻尼的情况下，方程式（3.44）变为非联立的独立运动方程，就像单自由度系统那样，可以很容易地求出各个模态响应，然后利用模态叠加法，可以得到实际的响应。

如果模态阻尼矩阵不是对角矩阵，则式（3.44）依然为相互耦合的联立方程，可以用直接法求解。但是，通过舍去高频模态，可以大幅降低联立方程的个数，从而达到提高计算效率的目的。例如如果采用前p个模态进行计算，则n个联立方程缩减为以下p个联立方程（p<<n）

这里介绍MSC.Nastran所采用的方法求解方程式（3.45）。利用差分原理，可以得到模态速度和模态加速度响应为

引入3个时刻的平均值

方程（3.45）变为

整理可得

这里

利用第5章介绍的线性代数方程组的求解方法，通过对矩阵[a₁]分解，可以求得模态响应，然后代回式（3.42），可得真正的响应。

如果[C]为对角阵（比例阻尼的情况），则[a₁]为对角阵，无需矩阵分解，即可直接计算。事实上，这时，方程（3.45）变为以下独立的方程(www.xing528.com)

或变形为

其中，ω_k是k阶模态的固有频率，ζ_k是k阶模态的阻尼比。直接利用第1章中介绍的杜哈梅积分公式（Duhamel’s Integral），可得方程式（3.46）的解为

这里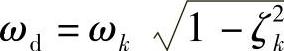，是有阻尼固有频率，α_k、β_k由初始条件决定

根据式（3.42），得

{x（0）}=[ϕ]{δ（0）}

假定对[ϕ]进行了质量正规化，则给上式两边同乘以[ϕ]^T[m]，可得

即模态坐标上的初始值可以从物理坐标上的初始值得到。

最后，介绍利用傅里叶逆变换求解瞬态时间响应的方法。在某些情况下，只能得到动载荷的频率特性，如飞机机翼的空气动力学载荷。这时，可以先求出频率响应，然后利用傅里叶逆变换求出相应的瞬态时间响应。此外，对于具有周期性的动载荷，也可以利用此法。

该方法的本质是频率响应分析。预先计算出激励点a与响应点b之间的传递函数H_ab（ω），再把时域激励力F_a（t）转换到频域去

则b点的频率响应为

X_b（ω）=H_ab（ω）F_a（ω）经过傅里叶逆变换，得到所要的时间响应

这个方法的一个好处是可以直接处理结构阻尼。另外，在某些有限元模型中，可能包含有结构阻尼以外的复数成分（如用复数弹簧表现的传递函数子结构模型），这样的系统也无法利用数值积分求解时间响应。傅里叶变换方法提供了一个变通的解法，但应注意，由于不是直接在时域求解，该方法不能表现随时间变化较大的现象，如发散振动等。