用剩余向量法进行补偿模态截止误差的优化方案

上面指出了模态截止带来的误差问题，其中，由高频模态引起的剩余刚性是利用模态法计算结构动力响应的主要误差来源。当然，最直接了当的提高精度的方法就是在计算中把更多的高频模态采用进来，但这样做会增加计算时间和成本。事实上，对于大规模系统来说，前面所说的“选取所需频率上限的2倍以上的模态参与计算”，都会因为计算时间的制约不好运用。例如对于有内装饰的车体模型（Trimmed Body），在1Hz的频率间隔上可能存在数个模态，但如果要计算0～200Hz的频率响应而采用高至400Hz的固有模态参与计算的话，可能要增加数百甚至上千个模态，这无疑会带来很大的计算负担。合理的做法是：只计算出截至200Hz的固有模态（或稍微高一些的频率，如250Hz），然后利用剩余向量法对舍掉的高频模态的影响加以补偿。这个方法的基础就是Hansteen法。

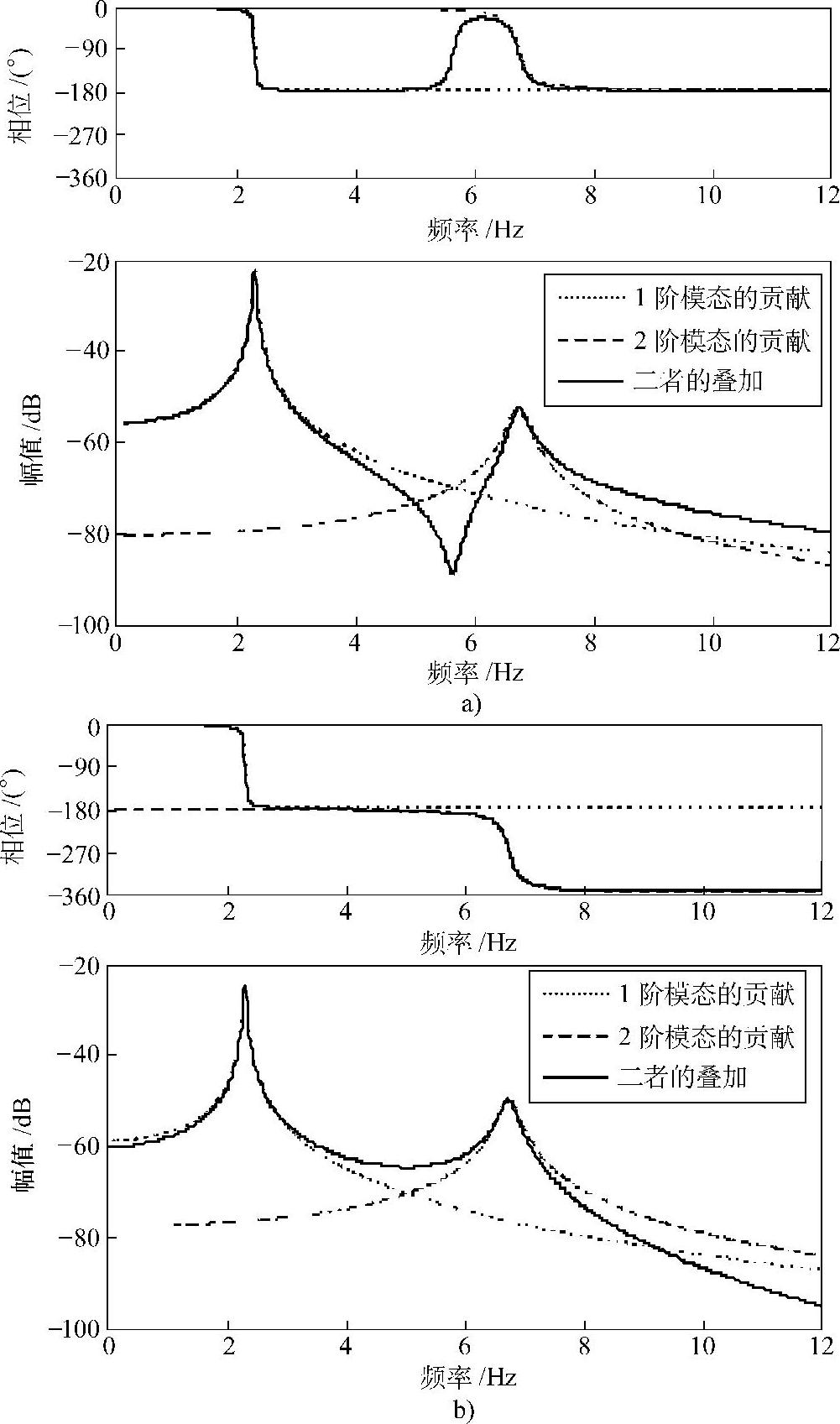
图3.7 模态叠加法算出的二自由度系统的柔顺性函数

a）驱动点柔顺性函数（Driving Point Compliance）

b）传递柔顺性函数（Transfer Compliance）

对于一个n自由度系统，利用模态坐标变换可得，其强迫振动方程为

[ϕ]^T（-ω²[m]+jω[c]+[k]）[ϕ]{δ}=[ϕ]^T{F} （3.38）

可以按照模态频率的高低，将模态矩阵划分为[ϕ]=[ϕ_lϕ_h]。其中，[ϕ_l]表示需要的低频模态，[ϕ_h]代表舍掉的不直接参与响应计算的高频模态。于是，式（3.38）右边可以写成

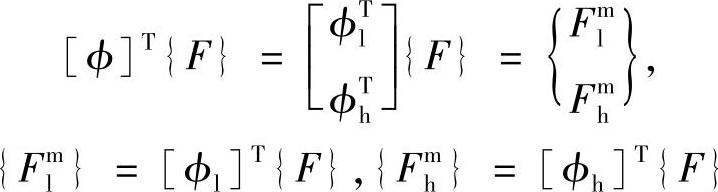
其中，{F^m_l}、{F_h^m}分别代表低频模态力和高频模态力。

此外，对于经过质量正规化的模态向量，根据模态的正交性，有以下关系

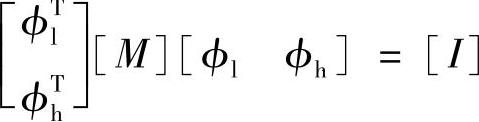
利用以上关系，可以得到以下等价变换(www.xing528.com)

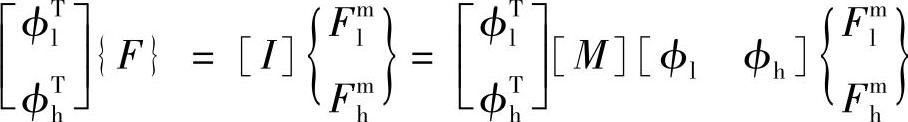
可见，激励力向量可以表示为

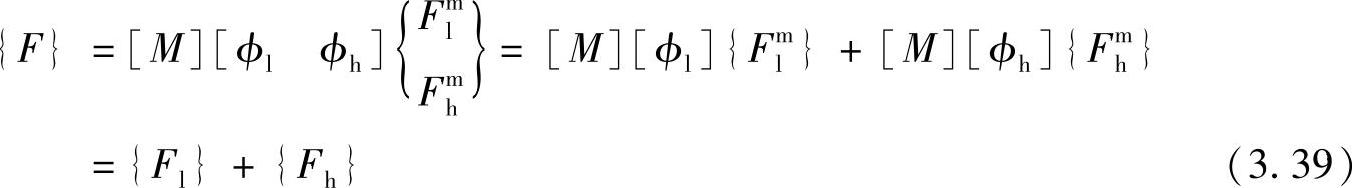
式（3.39）代表的物理意义是：可以把激励力向量分解为只激励起低频模态的成分{F_l}和只激励起高频模态的成分{F_h}（注意：向量的长度是一样的）。所谓的模态截止误差，就是因为忽略掉了由{F_h}激励起的高频模态的响应而引起的。由式（3.39）可以得到{F_h}为

{F_h}={F}-[M][ϕ_l]{F_l^m}

进一步将{F^m_l}=[ϕ_l]^T{F}代入，可得

{F_h}=（[I]-[M][ϕ_l][ϕ_l]^T）{F}

由该激励力成分引起的系统响应为

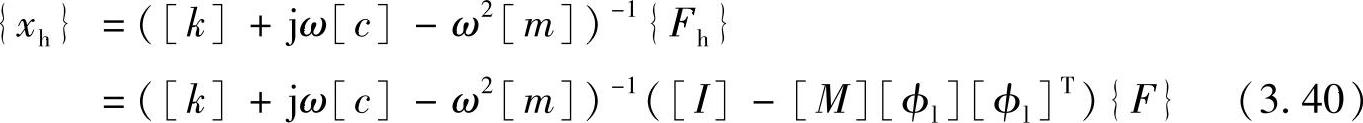
对于需要计算响应的所需频率来说，舍掉的高频模态的固有频率远远要高，即ω<<Ω_h。高频模态的影响主要表现在其刚性控制区，因此，式（3.40）可以近似为

{x_h}=[k]^-1（[I]-[M][ϕ_l][ϕ_l]^T）{F}=[D]{F} （3.41）这就是所谓的剩余向量，或称为剩余模态。[D]=[k]^-1（[I]-[M][ϕ_l][ϕ_l]^T）的倒数就是剩余刚性。式（3.41）表明，根据计算得到的低频模态[ϕ_l]，即可预测出舍掉的高频模态的影响，从而对通过低频模态叠加而成的响应结果进行补偿。

在MSC.Nastran中，上述剩余向量法（Residual Vector Method）已成为模态法动力响应计算（频域及时域）的标准选项。