给定外部激励力的大小和频率特性,就可以按3.4.1节中的方法求出实际的结构响应。但是,在动力学分析当中,更多的是研究系统的频率响应函数(Frequency Response Function,FRF),即加振点与拾振点之间的传递函数。如果加振点与拾振点位置一致,则称为驱动点频率响应函数;否则,称为传递频率响应函数。频率响应函数相当于单位激励力下的频率响应。这种不考虑外力的具体特性的传递函数分析方法有助于在产品开发初期阶段,外载荷还不明确的情况下研究结构的动态特性,为采取有效的对策提供依据。
常用以下3种形式的频率响应函数
① 柔顺性函数(Compliance):位移/力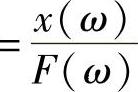 。
。
② 导纳函数(Mobility):速度/力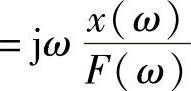 。
。
③ 惯量函数(Inertance):加速度/力=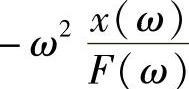 。
。
图3.5所示为一个单自由度系统的3种频率响应函数。其中,导纳函数和惯量函数是根据柔顺性函数计算得来的。频率响应函数可以大致分为3个领域:小于共振频率的领域刚性的影响较大,称为刚性控制区;大于共振频率的领域质量的影响较大,称为质量控制区;共振频率附近的领域阻尼影响大,称为阻尼控制区。工程上,常把远离共振频率的刚性控制区的曲线称为刚性线(Stiffness Line),把远离共振频率的质量控制区的曲线称为质量线(Mass Line)。
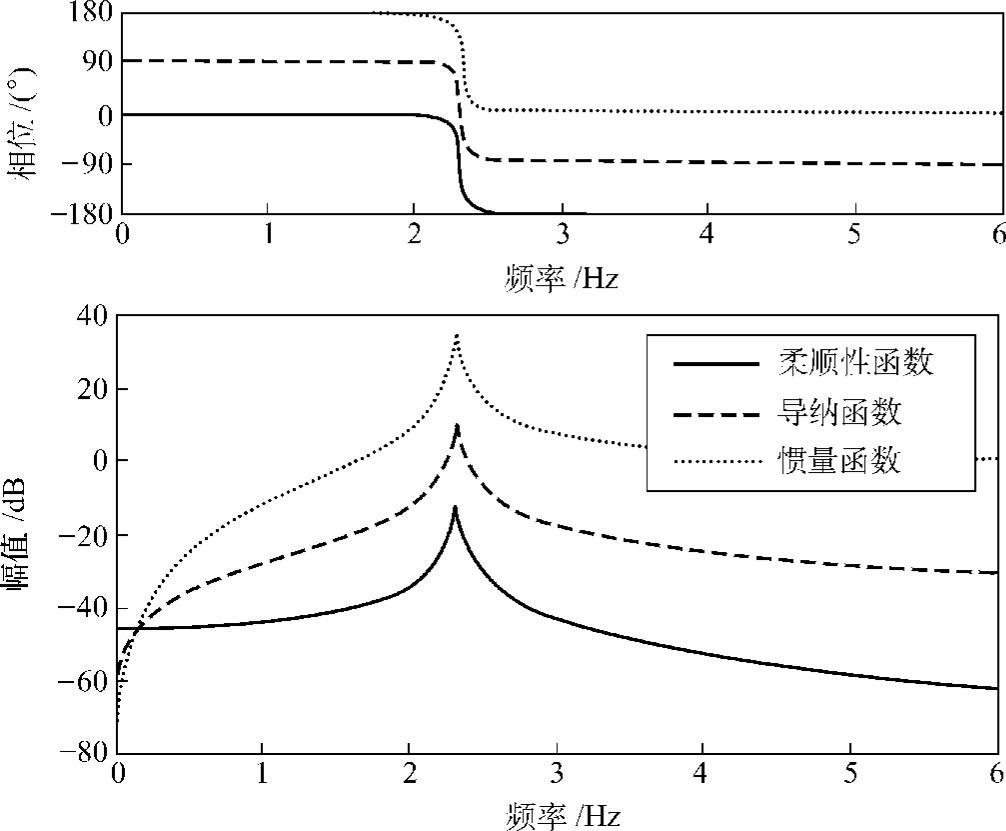
图3.5 频率响应函数
为了理解频率响应函数的特性,我们考虑比例阻尼的情况。假定激励力作用在a点,响应观察点在b点,由方程式(3.29)可得
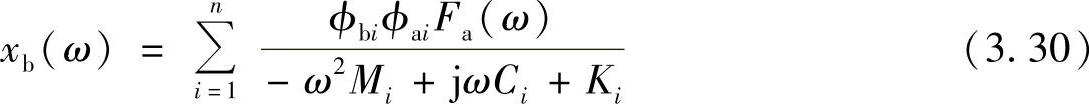
定义
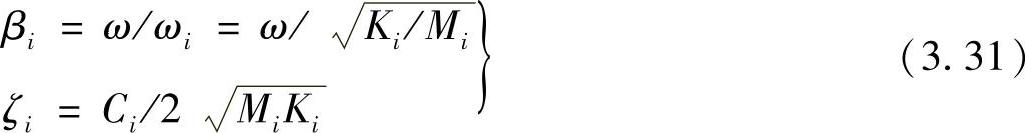
则式(3.30)变形为
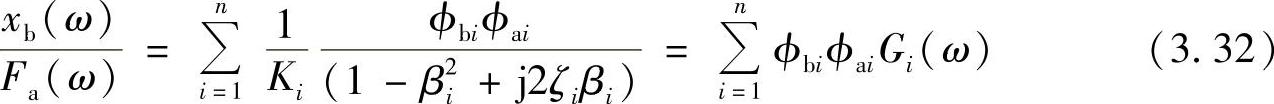
这里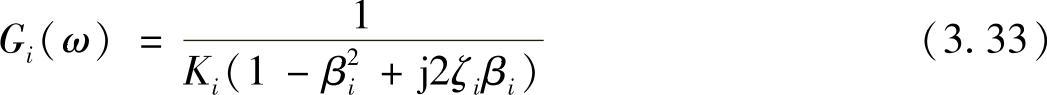
称为第i阶模态的传递函数。式(3.32)的关系如图3.6所示。
式(3.32)显示,若把加振点与响应观察点位置对换,所得的频率响应函数不变。这个性质称为传递函数的互换性原理(Reciprocity),是线性系统的重要性质。在模态分析实验中,常常利用这个性质来检查对象结构的线性,从而判断测量结果的可靠程度。另外,利用这个性质,还可以在激振器无法安置的情况下测量到相应的传递函数。例如在研究轿车的噪声敏感度时,需要对悬架与车体的各个结合点进行加振,并测量车室内的噪声,二者之间的传递函数就是噪声敏感度。由于空间限制,在某些位置可能无法加振。相反,利用互换性原理,用扬声器在车室内对声场进行激励,在悬架与车体的结合点位置安装上加速度传感器,可以一举测量到各点的振动,从而可以提高测量效率。
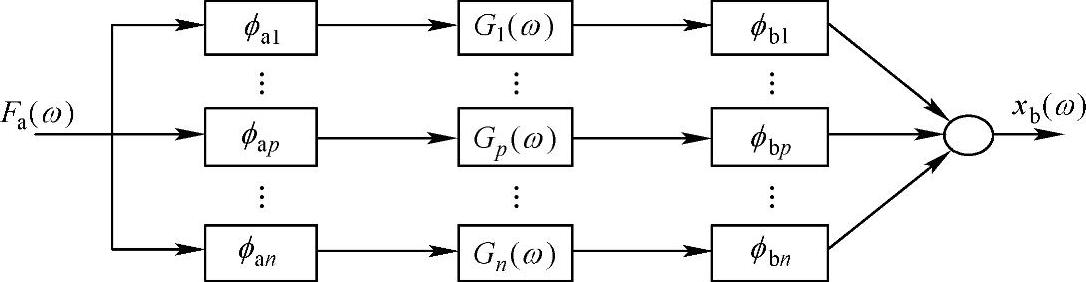
图3.6 频率响应函数的方块图表示
此外,式(3.32)还可以改写为(https://www.xing528.com)
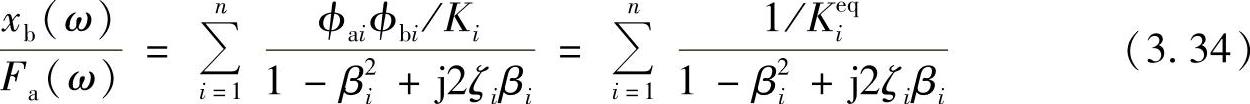
其中,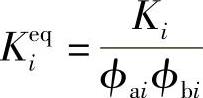
称为第i阶模态的等价刚性。这是从激励点到响应点之间的表象刚性。模态刚性Ki与位置无关,但等价刚性Kieq则是位置的函数。如果加振点处于模态的节点(ϕai=0),或者观测点处于模态的节点(ϕbi=0),则等价刚性为无限大。
根据模态等价刚性,可以定义模态等价质量为
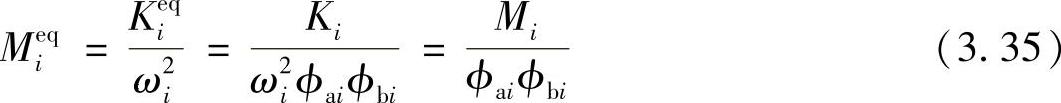
如果对模态向量进行了质量正规化处理,则模态质量Mi=1,式(3.35)成为

显然,这个值也随着位置而变化。
现在我们来讨论模态截止的问题。式(3.34)可以写为
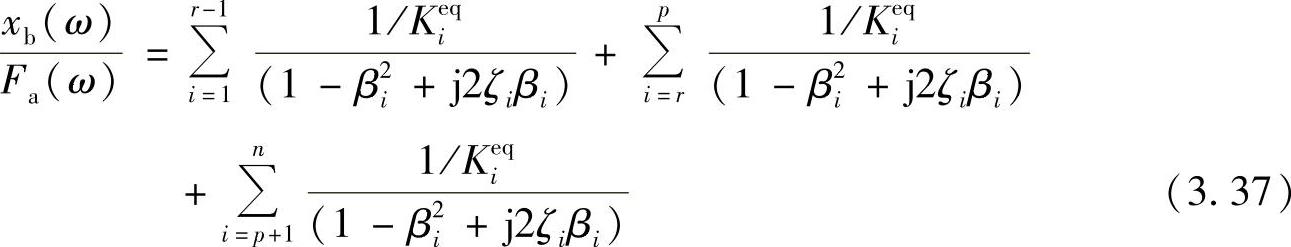
如果我们只保留由r阶到p阶的模态参与式(3.37)的计算,则引起的误差有两部分。第一部分是r阶以下的模态所引起的,对应于式(3.37)中右边的第一项。这时,可认为βi=ω/ωi>>1,因此有以下简化
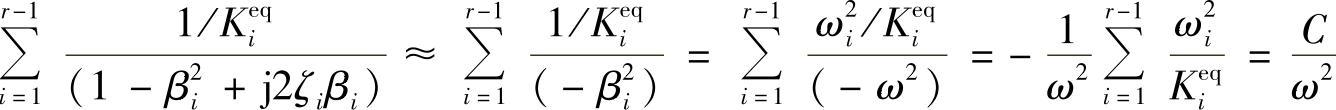
这里,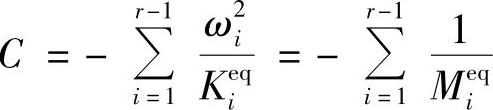 是一个不随频率变化的常数,其倒数的量纲为千克,因此称为剩余质量。另一方面,p阶以上模态引起的高频误差为(βi=ω/ωi<<1)
是一个不随频率变化的常数,其倒数的量纲为千克,因此称为剩余质量。另一方面,p阶以上模态引起的高频误差为(βi=ω/ωi<<1)
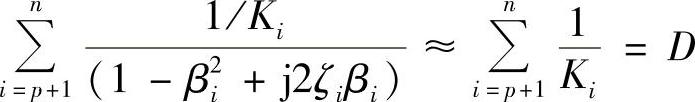
其中,D也是一个常数,其倒数称为剩余刚性。
在有限元分析中,一般从最低阶模态算起,因此不会引起剩余质量的误差问题。但是,对于大规模系统,几乎肯定要舍去高频模态,从而产生由剩余刚性引起的误差。为了补偿模态截止引起的误差,在计算频率响应时常采用剩余向量法(Residual Vector Method)。详细内容在下一小节中介绍。
这里,以图3.3所示二自由度系统为例,来说明频率响应函数的计算。通过模态分析并采用模态向量的质量正规化方法,得到以下模态参数
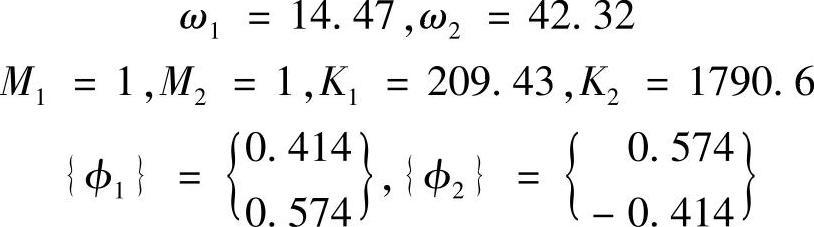
假定第一阶模态的阻尼比为0.02,第二阶模态的阻尼比为0.01,利用式(3.32)所示的模态叠加法可以算出柔顺性函数,如图3.7所示。图3.7a为质点2的驱动点柔顺性函数,图3.7b为由质点2到质点1的传递柔顺性函数。图中,点线为只有第一阶模态存在时的结果,虚线为只有第二阶模态存在时的结果,实线是二者的叠加结果。在驱动点柔顺性函数中,两个峰值之间有一个深谷,这是由两个模态逆相抵消引起的,称为反共振点(Anti-resonance);但在传递柔顺性函数中,在两个峰值之间的频段上,两个模态同相,没有反共振点。作为一般性结论,对于驱动点柔顺性函数,在两个相临的峰值之间必然存在一个反共振点;但对于传递柔顺性函数来说,反共振点不一定存在。利用这个性质,可以定性地判断得到的频率响应函数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




