结构动力学中的模态坐标转换与叠加法

模态的正交性使得各个模态之间完全分离，没有耦合。这个性质引出了一个重要的坐标变换。由矩阵理论可知，一组长度为n的正交向量构成了一个基底，任何一个长度为n的向量都可以由这组正交向量的线性组合得来。既然我们通过特征值分析得到了模态向量这组正交向量，当然可以设想物理坐标上的响应可以由模态向量的组合得到，即

这里，模态矩阵[ϕ]包含了所有特征向量，{q}是一个系数向量。将式（3.19）代入到式（3.9），

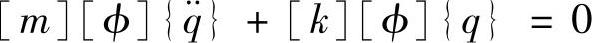
两边同乘以[ϕ]^T，并利用正交性关系式（3.14），得

由于[M]和[K]为对角矩阵，式（3.20）等价于以下n个独立方程(www.xing528.com)

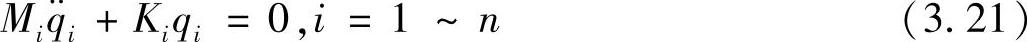
这些相互独立的微分方程代表了n个单自由度系统（SDOF）。相对于在物理坐标上表示的联立方程组（各个方程之间存在耦合），式（3.21）代表的是一组解耦后的非联立方程。显然，求解方程式（3.21）非常方便。将得到的{q}代入到方程式（3.19），即可求得真正的响应。这里，我们把{q}称为模态坐标上的响应，或称模态坐标。

由于求解方程式（3.21）比求解方程式（3.9）要容易得多，由式（3.19）所代表的坐标变换在结构动力学分析中非常重要。把物理坐标上的联立方程组转换到模态坐标上的非联立方程进行计算的方法称为模态叠加法，或简称模态法。相对于直接解法，模态法的计算效率非常高。

图3.4所示为物理坐标上的二自由度系统转换为模态坐标上的二单自由度系统的示意图。

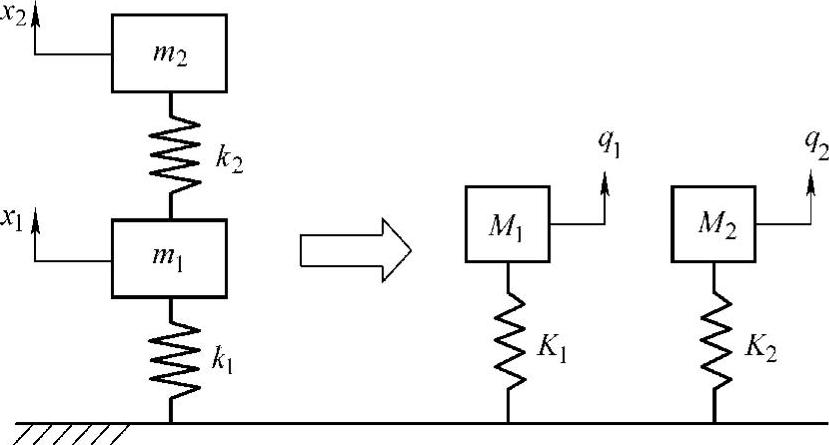
图3.4 物理坐标上的二自由度系统转换为模态坐标上的二单自由度系统