模态向量的正交性优化

首先考察上面二自由度系统的例子。该系统的模态形状矩阵为

计算[ϕ]^T[ϕ]，可得

进一步考察非对角线上的元素的值（将ω²₁、ω²₂的结果代入）

可见，非对角线上的元素为零。也就是说，矩阵[ϕ]^T[ϕ]为对角阵。它表明各个模态向量相互独立，不存在耦合。这个性质称为模态向量的正交性。

通常，模态向量的正交性（Orthogonality）用以下形式表示

其中，M_i、K_i分别称为第i阶模态的模态质量和模态刚性。显然，对模态向量进行质量正规化处理就是做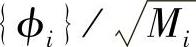的运算，这样可以满足式（3.13）。以上关系写成矩阵的形式为

其中，[M]称为模态质量矩阵，[K]称为模态刚性矩阵，二者皆为对角阵。也就是说，利用模态矩阵对质量和刚性矩阵进行相似变换，可以把它们变为对角阵。以下对该性质做一证明。

对于模态i和模态j，由式（3.10）可得

给式（3.15）两边同乘以{ϕ_j}^T(www.xing528.com)

由于[m]、[k]为对称矩阵，通过矩阵转置上式可以变为

然后给式（3.16）两边同乘以{ϕ_i}^T，得

式（3.18）减去式（3.17），得

如果ω_i≠ω_j，则有{ϕ_i}^T[m]{ϕ_j}=0，进而有{ϕ_i}^T[k]{ϕ_j}=0。

以上证明是在特征值没有重根的情况下进行的。即使有重根，正交性的结论也是成立的。事实上，对于一个实对称矩阵[A]，必然存在一个正交矩阵[R]，使得变换[R]^T[A][R]=[Λ]成立。其中，[Λ]为对角矩阵，其对角线上的元素为矩阵A的特征值λ_i（i=1～n）。这个结论在数学上有严格的证明，不管λ_i是否有重根。

由上面的式（3.17）可得

这个关系式称为瑞利方程（Rayleigh’s Equation），或瑞利商。由此可见，一个模态可以当作质量为M_i、刚性为K_i的单自由度系统来看待。