研究系统振动的固有特征,出发点是无阻尼自由振动。其运动方程式为

这里,[m]、[k]为(n×n)阶实对称矩阵。假定以上方程的解为简谐振动,则
{x}={ϕ}e jωt
代入式(3.9),可得
([k]-ω2[m]){ϕ}=0(3.10)
在数学上,上式称为一般化特征值问题(参见第5章)。可以把它转化为以下标准特征值问题
([A]-λ[I]){ϕ}=0 (3.11)
这里,[A]=[m]-1[k],[I]为单位矩阵,λ=ω2。
方程式(3.11)的λ称为系统的特征值,{ϕ}为与之相对应的特征向量。方程式(3.10)或(3.11)的一个显而易见的解是{ϕ}=0,这对应于系统停止状态,因此没有实际意义。在{ϕ}≠0的条件下,方程式(3.10)的解必须满足以下行列式为0的条件
[k]-ω2[m]=0 (3.12)
这是一个线性代数方程,求解它可以得到一系列ωi(i=1,2,3,…),即系统的固有频率。进而由方程式(3.10),可以得到与之对应的特征向量{ϕ}。对应于每一个ωi,有一个特征向量{ϕi},它反映了模态的形状,因此也称模态向量。把所有的特征向量放在一起,可以构成一个特征向量矩阵[ϕ],也称为模态矩阵。
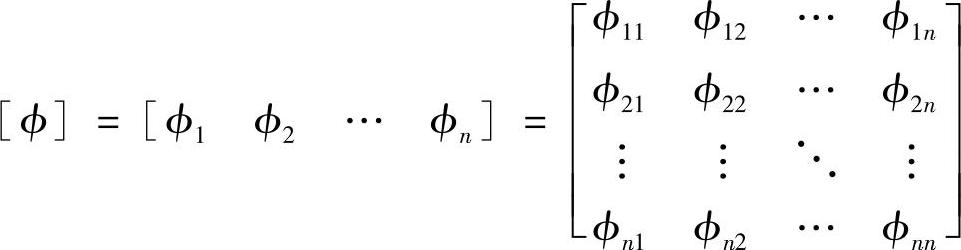
特征值求解方法大体可以分为矩阵相似变形法和迭代法。前者是根据矩阵的相似变形把矩阵[A]=[m]-1[k]变换成对角矩阵,从而一举得到所有的特征值和特征向量;后者则是利用迭代解法逐次求解所需要的特征值和特征向量。把二者的优点结合起来的混合法是目前有限元分析中的主要解法,其代表就是Lanczos法。
关于特征值分析的详细介绍,请参见5.4的内容。这里,以一个二自由度系统为例,举例说明特征值及特征向量的概念。
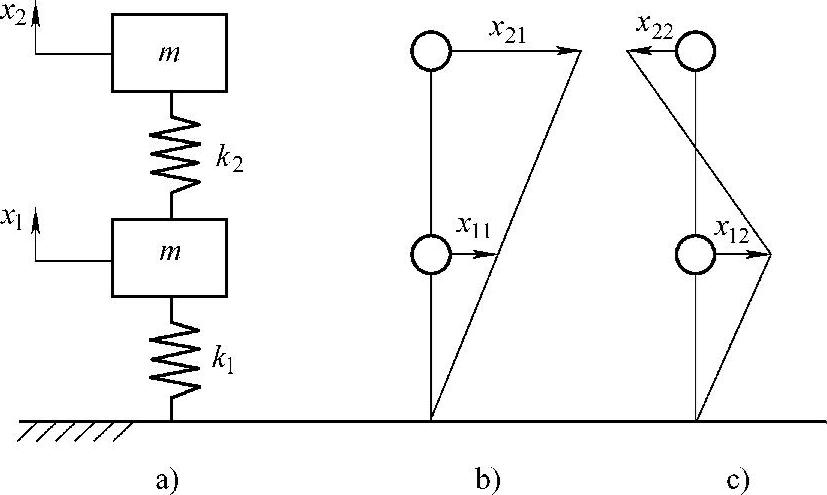
图3.3 二自由度系统(为便于表示,模态变形在水平方向画出)
a)物理坐标 b)1阶模态 c)2阶模态
图3.3所示的二自由度系统的自由振动由以下方程决定
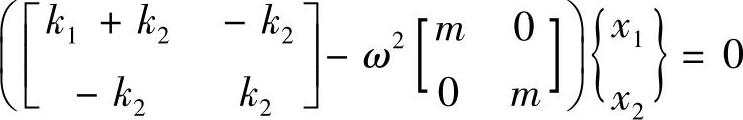
容易求得对应的特征值为
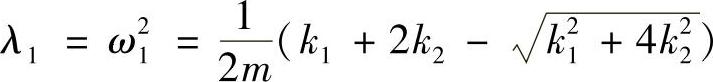 (https://www.xing528.com)
(https://www.xing528.com)
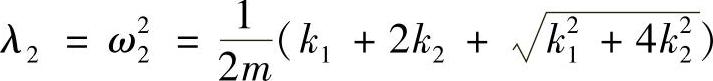
对应于ω1,特征向量为{ϕ1}={x11x21}T,满足以下方程
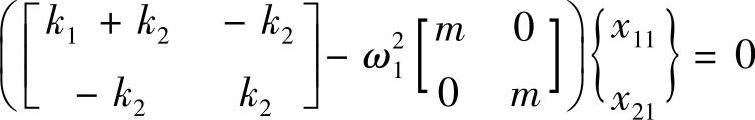
即
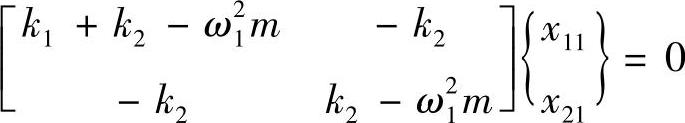
将特征值ω21的表达式代入,可以证明以上方程的系数矩阵的行列式为0,所以{ϕ1}={x11x21}T的非零解不唯一。x11和x21有无限个解,只要它们的比满足以下关系
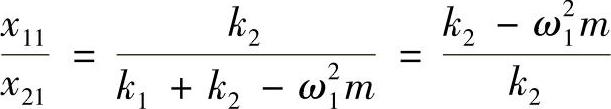
这就是特征向量的特点,即由特征向量代表的模态形状表示的是一个相对变形的关系。同样,对于2阶模态的固有频率ω2,可以得到对应的模态向量{ϕ2}={x12x22}T,满足下列比例关系
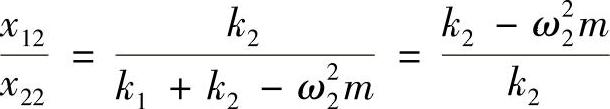
如果将质点2的模态变形进行正规化,则模态形状可以用以下矩阵表示
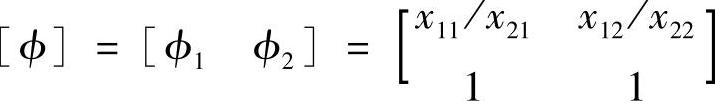
如果取m=2.0kg,k1=1000.0N/m,k2=1500.0N/m,则有
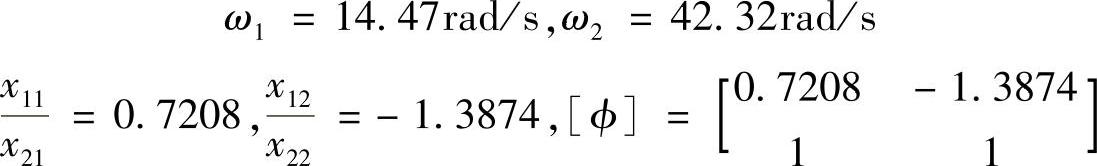
可见,1阶模态两个质点的振动同相,而2阶模态的两个质点的振动反相。模态形状如图3.3b和图3.3c所示(为便于表示,模态变形在水平方向画出)。
再次指出,不能混淆物理坐标上的响应(x1,x2)与模态变形(x11,x21;x12,x22)。前者是绝对量,其大小反映的是真实的变形;而后者是相对量,其大小仅表现一种相对的变形关系。
尽管模态向量可以任意放大缩小,通常按两种方法对其进行正规化处理。一种是质量正规化方法,即使模态向量满足以下关系
{ϕi}T[m]{ϕi}=1.0(3.13)
例如上面例子的模态形状经过质量正规化后变为
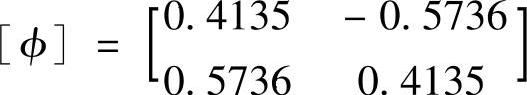
另一种是最大值正规化方法,即使模态向量中的最大变形为1,这样,模态形状被限制在区间[-1.0,1.0]上。例如上面的例子经过这种正规化后成为
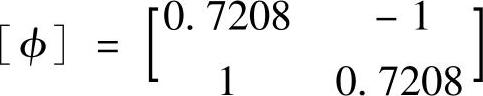
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




