瞬态时间响应优化方法

在上面的稳态响应分析中，我们假定激励力的大小和频率特征是稳定的。本节中，我们要讨论激励力随时间快速变化的情况，例如突然产生的冲击力等。瞬态激励（Transient Excitation）的含义是指经过一个短暂时间就消失掉的激励力，这里我们泛指幅值随时间快速变化的激励力。这时，我们假定激励力随时间变化的关系可以明确地给出，于是，时域里的运动方程为

在求解频率响应时，把微分方程式（3.3）转化成了代数方程来求解。在时域里求解上述方程时，同样需要把它转化为代数方程，这需要利用数值积分的方法。最直接的方法就是利用中央差分原理。

设积分步长为Δt（通常是固定的），则速度和加速度可以由差分方法得到

代入到式（3.6）整理，可得

在此定义

得

这个方程显示，时刻i+1的响应可以由时刻i及时刻i-1的结果得到。这是典型的显式多步法（参见第5章）。

通常，启动多步法需要先求出两个时刻的值以后才可以进行。具体地说，假定0时刻的值{x₀}已知，还需要知道在此之前的一个时刻的值{x_-1}。这里，我们利用初始条件来确定这个值。设系统的初始值为{x₀}、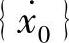、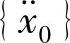，则利用差分方法可得

由此可以求得

求解方程式（3.7），需要对矩阵[a₁]进行三角分解（关于矩阵的三角分解，请参阅5.2节的内容），也就是需要对质量矩阵和阻尼矩阵进行分解，但不需要对刚性矩阵进行分解。如果不考虑阻尼，且质量矩阵为对角阵（通常如此），则方程式（3.7）已经解耦，不需要对[a₁]进行分解，可以直接得到方程的解，计算效率非常高。这是中央差分法的主要优点。

但是，作为显式解法，中央差分法的缺点是积分步长必须满足小于临界步长Δt_cr的条件

Δt≤Δt_cr=T_n/π=2/ω_n其中，T_n为系统的最小振动周期，ω_n为与之对应的最大角频率。如果积分步长大于这个临界值，则结果发散。这个性质称为数值积分的条件稳定性。条件稳定性可以从一个极端情况看出：考虑质量为0并且阻尼为0的特殊情况。这时，系数矩阵[a₁]为0，为了满足方程式（3.7），{x_i+1}必须为无穷大。事实上，此时T_n=0，无论Δt取多小的值，都无法满足稳定性条件，结果都发散。显式解法的条件稳定性限制了可采用的积分步长，对于质量很小而刚性很大的系统，T_n很小，积分步长Δt也应很小，计算效率会很低。(www.xing528.com)

为了克服临界步长的限制，可以采用无条件稳定的隐式解法。这里，我们介绍MSC.Nastran所采用的方法。引入以下位移及作用力在3个时刻上的平均

整理后，可得以下新的方程

这里，新的系数矩阵定义如下：

由于方程右边含有i+1时刻的载荷，该解法属于隐式解法，积分步长不受临界值的限制。例如考虑[m]=0与[c]=0的特殊情况，这时，方程式（3.8）变为

[k]{x_i}={F_i}

这是一个静力平衡方程，解是存在的，不像显式解法那样变得不稳定。

该解法的另一个特点是还需要对刚性矩阵进行分解（因为系数矩阵[A₁]中含有刚性矩阵）。这点会增加计算的成本，是隐式解法的一个缺点。如果Δt固定，则只需要一次分解即可；如果Δt变动，则需要重新分解，使计算负荷进一步增大。

计算开始时，设初始加速度为0，初始位移和初始速度分别为x₀、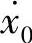，则可以决定{x_-1}、{F_-1}、{F₀}如下：

最后需要指出的是，上述系数矩阵必须是实数矩阵才可以进行以上运算。也就是说，如果存在结构阻尼的话，不能像频率响应分析那样用刚性的虚部来表示，而应该先把它转化为等价的粘性阻尼，从而并入阻尼矩阵[c]中去。

应注意，尽管隐式解法对于Δt没有上限要求，实际上Δt应该足够的小，以能够精确地表现动载荷的频率特征。一般取Δt≤0.1T_min，T_min为动载荷的最短周期。

同频率响应分析的直接解法一样，对大规模系统来说，瞬态时域响应的直接解法运算量也很可观。