多自由度系统的运动方程介绍

在第1章的概述里我们已经说过，实际的机械结构都是连续的弹性体，理论上具有无限多的自由度。除了较为简单的情况，例如简单边界条件下的弦、梁的振动，可以从求解微分方程得到精确解以外，一般需要对研究对象进行离散化处理，建立有限多个自由度的低阶模型。有限元分析方法就是一种典型的离散化方法。图3.1所示为用不同自由度的离散模型来表现悬臂梁不同振动形态的示意图。

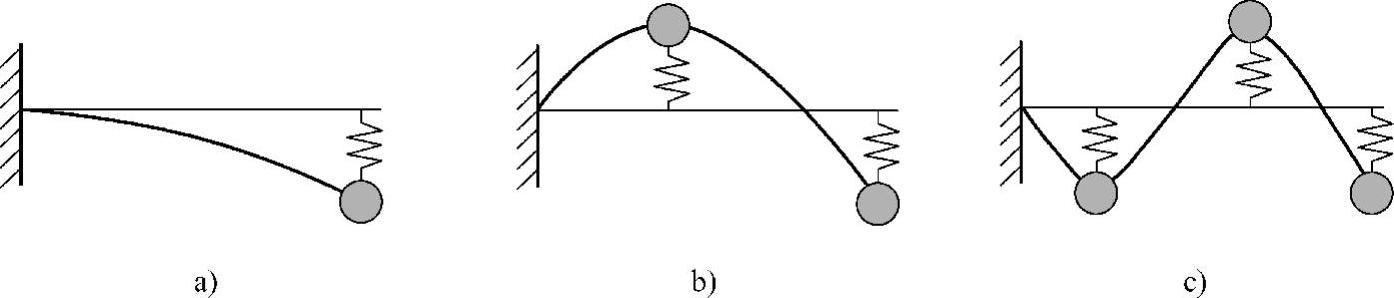
图3.1 用不同自由度的离散模型来表现悬臂梁的不同振动形态

a）一自由度近似 b）二自由度近似 c）三自由度近似

简单地说，离散化就是利用集中力学元件（质量，弹簧，阻尼）的组合来表现连续分布的质量及刚性等力学特性。离散化的过程其实是一个力学模型的建立过程。我们暂不讨论离散化的具体方法，而直接以离散化后的系统为对象，来探讨多自由度系统的振动问题。

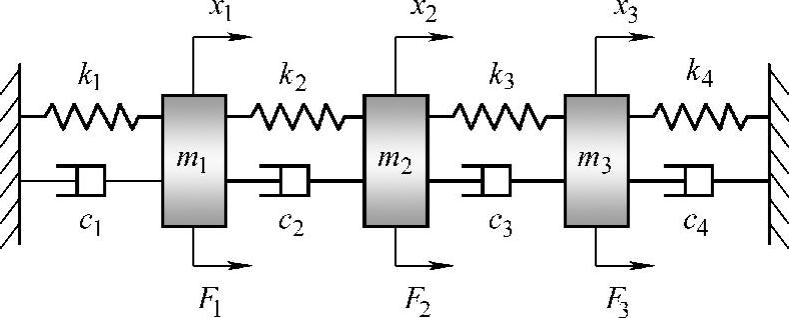
图3.2 一个三自由度振动系统的力学模型

图3.2所示为一个三自由度振动系统。三个集中质量（质点）由弹簧及阻尼元件连接起来。在外力F作用下，对于每一个质点，列出其动力平衡方程，可得下列方程组

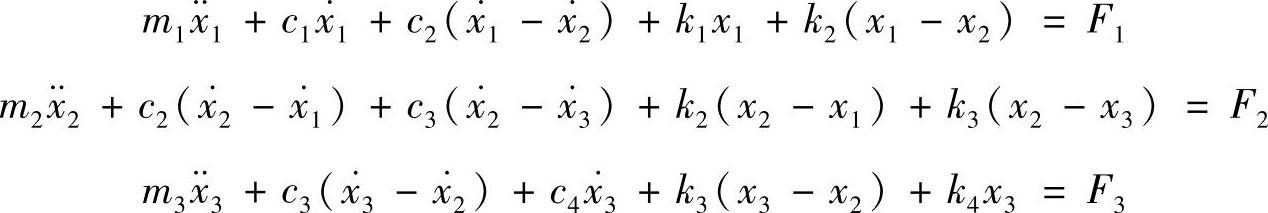
整理后，得到以下用矩阵形式表示的运动方程

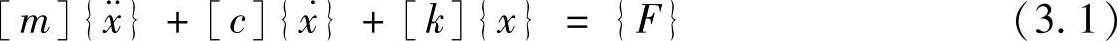
其中，(www.xing528.com)

式（3.1）虽然是针对一个三自由度系统得到的，但其形式代表了多自由度系统的运动方程的一般形式。

以上方程是根据牛顿运动定理得来的。对于复杂的系统，更为有效的推导系统运动方程的方法是拉格朗日法（Lagrange’s Method）。其表达式为

这里，L=T-U，T、U、D分别代表系统的动能、势能和耗散能；q_i（i=1～n）为一般化坐标；Q_i（i=1～n）为一般化力。对于n自由度系统，有以下定义

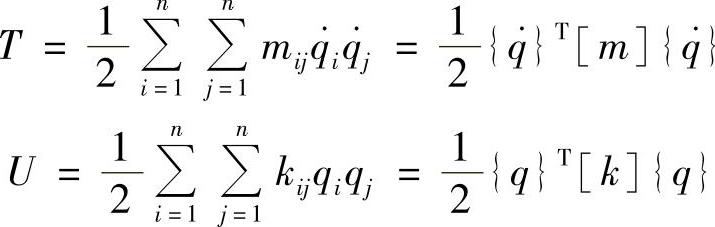
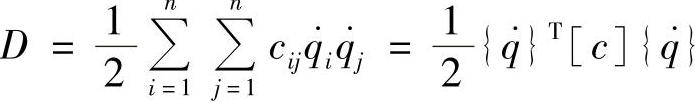
于是有

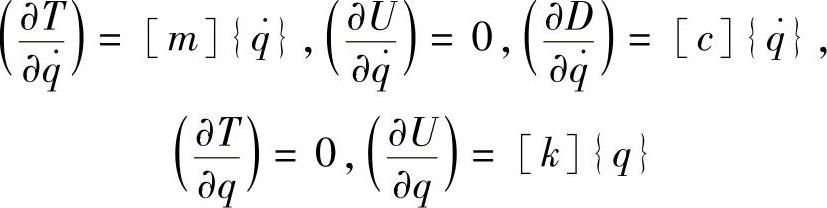
令q_i=x_i、Q_i=F_i，将以上关系代入式（3.2）整理，即可得到式（3.1）。