主动隔振系统：优化机械设备稳定性

在精密加工以及精密测量中，隔离外界的背景振动的干扰是一个重要的技术要求。隔振台就是针对上述需要而开发出的产品。一般的隔振台选用空气弹簧作为支撑元件，称为被动式隔振台。但是，单纯的被动式隔振台已不能满足日新月异的纳米制造等超精密技术的发展要求，需要导入主动隔振技术。在本节中，我们仍以单自由度系统为例，对主动隔振控制技术做一下介绍。

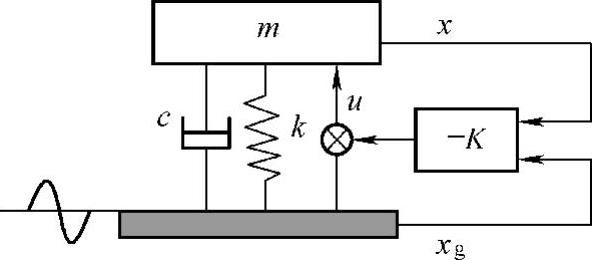
图2.64 主动隔振系统的力学模型

图2.64是主动隔振系统的力学模型。隔振台用一个刚体质量来代表，其振动位移用x表示，地面的背景振动用x_g表示。该系统的运动方程为

这里，考虑到一般的情况，F为作用在隔振台上的干扰力，u为主动控制力。对该方程进行变形，得

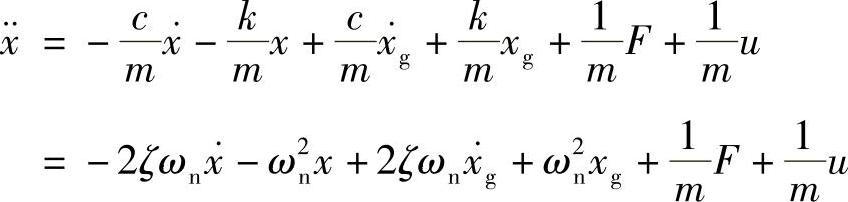
其中，隔振台的固有频率：；阻尼比：。

定义状态向量、输入向量和输出向量分别为

可得系统的状态方程为

其中，，，

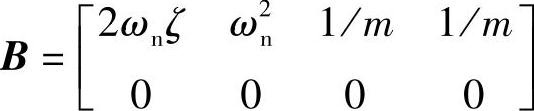
得到系统的状态方程后，可以应用最优控制理论设计出状态反馈控制。但是，作为举例，这里我们采用古典控制理论来设计主动隔振系统，思路仍然沿用前面介绍的刚体运动控制的方法，即在位移反馈系统中，引入速度反馈校正和PI校正环节。

图2.65是所设计的控制系统的Matlab/Simulink模型。其中，利用状态方程来表现如图2.64所示的力学模型。这里，把隔振台与地面的相对位移作为反馈信号。这样做一方面是因为检测相对位移容易一些，另一方面可以保证在极低频率上隔振台对地面运动的追踪性能。这在精密制造中是很有必要的，因为隔振台不光是要隔离掉高频干扰，还要保持与周边设备的相对位置不变。(www.xing528.com)

图2.65 单自由度系统主动隔振的Matlab/Simulink模型（avi—sdof）

图2.65中假定地面的位移已知，通过近似微分得到地面的速度，然后通过计算从地面到隔振台之间的振动传递率，可以方便地选择适当的增益。作为参考，表2.3给出所用的Matlab计算程序。

图2.66所示为振动传递率的计算结果。隔振台本身的固有频率定为1Hz，阻尼比为0.1。实线是在没有主动控制状态下的传递率，虚线是把阻尼比提高为0.2时的结果。可见，增加阻尼可以抑制共振频率处的振幅，但却降低了高频段的隔振效果。这就是2.2节所介绍的被动隔振系统的制约。作为对照，点线和点画线是在阻尼比为0.1时的主动控制的结果。可见，引入主动控制后，可以大幅度降低共振频率处的传递率，同时保证高频段的隔振性能不恶化。这就是主动隔振系统的最大优点。

实际的隔振台由3角支撑或4角支撑。作为主动控制的执行器，常用电磁式激振器。隔振台本身一般可以认为是一个刚体，在空气弹簧支撑下具有6个刚体自由度，即平移自由度X、Y、Z和旋转自由度R_x、R_y、R_z。所以，执行器的个数与位置应能保证这6个自由度可控。同样，选取的传感器的个数和安装位置应保证可以测量到这6个方向上的运动。旋转运动无法直接测量，只能通过两个同向而不同轴的平移运动量换算出来。例如在X方向布置1个传感器和1个执行器、在Y方向布置2个传感器和2个执行器、在Z方向上布置3个传感器和3个执行器，则隔振台的6个刚体运动完全可以控制。当然，为了降低硬件的成本，可以根据具体应用情况选择性地控制个别方向的运动，这样可以节省传感器和执行器的数目。近年来，隔振台的大型化和轻量化趋势导致其弹性模态较易被激励起来。因此，在控制器的设计中，一般应加上低通滤波器，使得刚体模态频率以上的控制力得到迅速衰减，以降低激励起隔振台弹性模态的风险。

表2.3 Matlab计算程序

（续）

图2.66 主动隔振控制的结果（凡例中的zeta代表阻尼比）

最后应该指出，如图2.65所示的单个方向上的控制系统可以方便地扩展到隔振台的六自由度控制中去。其方法是：先不考虑具体的传感器和执行器的位置，把目标定为隔振台的重心，根据重心的6个自由度可以计算出所需的作用在重心上的控制力（3个平进力，3个转矩）。这个过程可以在每个自由度上独立进行，就像图2.65所示那样。最后，只需根据刚体运动规律把重心位置的情报转换为各个传感器的响应，把计算出的作用在重心上的等效控制力分配到各个执行器中去即可。

利用计算机辅助工程（CAE）对包括控制系统特性在内的结构动特性进行分析，是目前产品开发中的重要技术手段。Matlab为控制系统的设计提供了便利的工具。一方面，根据有限元模型或机构解析模型得来的结构的动特性，可以用状态空间的表现方法纳入到Matlab/Simulink控制模型中去（如图2.65所示），从而可以在考虑上结构动特性的情况下对控制参数进行调整；另一方面，现有的主要商用结构及机构分析软件（如Nastran、Abaqus、Adams）都具有传递函数的表现功能，因此，也可以反过来把控制系统导入到有限元或多体动力学软件中来，例如MSC.Nastran中的TF（Transfer Function）和EPOINT（Extra Point）功能足以表现一般的控制系统的传递函数。这样，可以考察控制系统对结构动特性的影响，如不稳定的发散振动等。