主动动力吸振器的应用和优势

我们在2.3节介绍了传统的动力吸振器的原理。这种利用附加质量的被动式动力吸振器对于稳定的窄带振动很有效，但当系统特性发生变化以至于偏离最优同调频率时，减振效果会显著恶化，特别是当附加质量不大时更是如此。此外，当动力吸振器的质量给定后，最大的减振效果也就确定。要想获得更大的减振效果，只有增大吸振器的质量，这又与轻量化的要求相矛盾。为了解决这些问题，可以采用主动动力吸振器，如图2.61所示。

考虑到控制器在主振动系上施加作用力的同时，反作用力作用在吸振器上，该系统的运动方程为（这里，u为控制力信号）

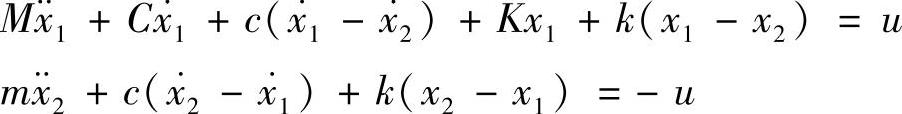
对上述运动方程进行变形

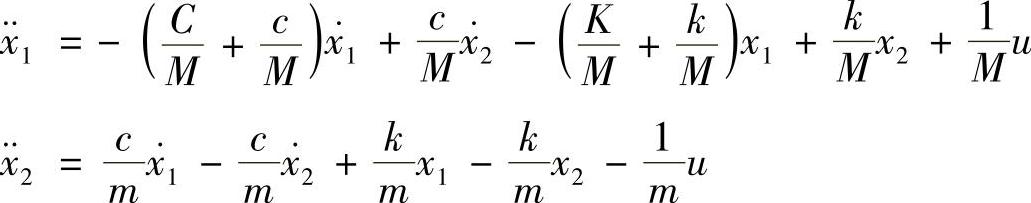
引入以下变量

质量比：μ=m/M

主振动系的固有频率：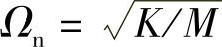

阻尼比：

吸振器的固有频率：

阻尼比：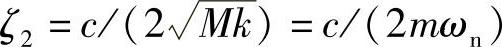

进一步整理，得

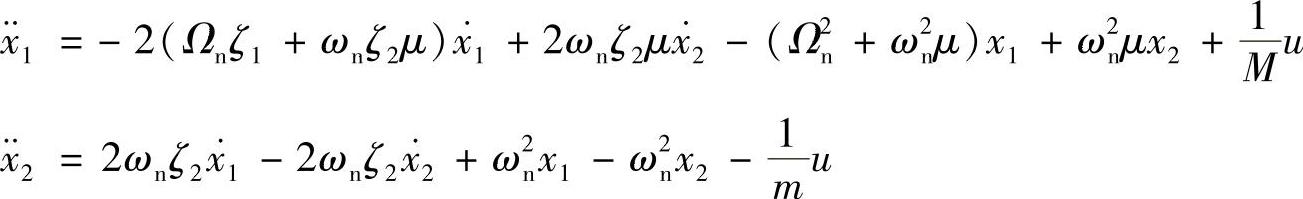
定义状态向量为

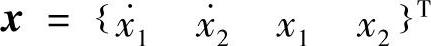
可得系统的状态方程为(www.xing528.com)

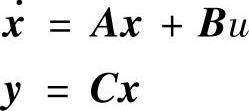
其中，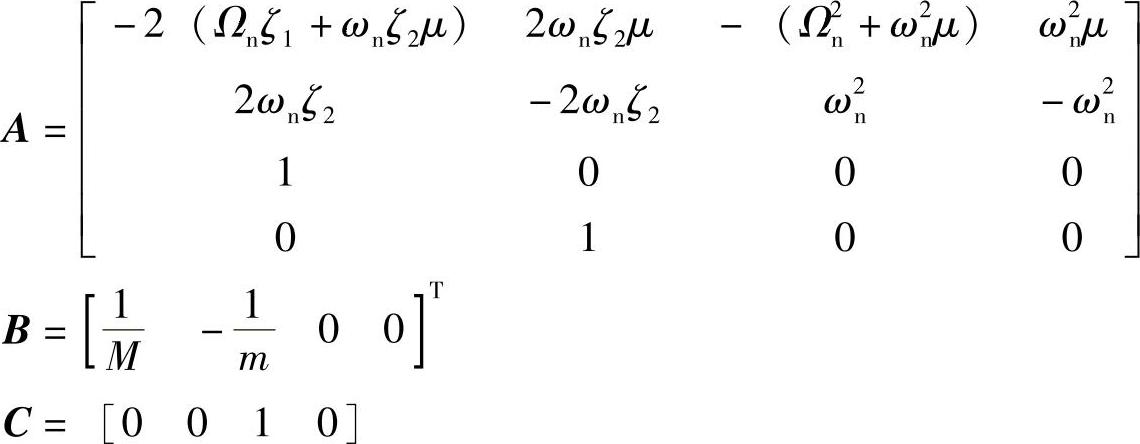

根据最优控制理论，控制信号u（t）应使以下二次型评价函数达到最小

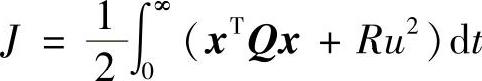
这里取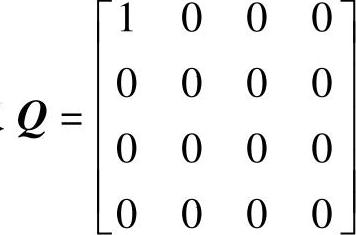，则，即把主振动系的动能作为最小化目标，通过求解Riccati方程，可以得到最优反馈增益矩阵。

作为举例，假设主振动系的阻尼很小，可以忽略，吸振器与主系的质量比μ=0.1，图2.61中的吸振器的弹簧刚性k由最佳同调频率决定[式（2.26）]，阻尼系数c由最佳阻尼决定[式（2.33）]。也就是说，被动动力吸振器本身处于最优设计状态。在此基础上，考察主动动力吸振器的效果。

图2.62为主振动系在冲击作用下的时域响应。其中，实线是被动动力吸振器单独作用下的结果，其余为在此基础上施加主动控制的结果。图2.63为主振动系的频率响应曲线。这里，沿用2.3节的表示方法，横轴为频率比，纵轴为振幅倍率。可见，利用主动控制可以大大提高振动的控制效果，而不需要增加吸振器的质量。此外，实践表明，即使主系的特性发生一定的变化，该方法仍能维持良好的控制效果。

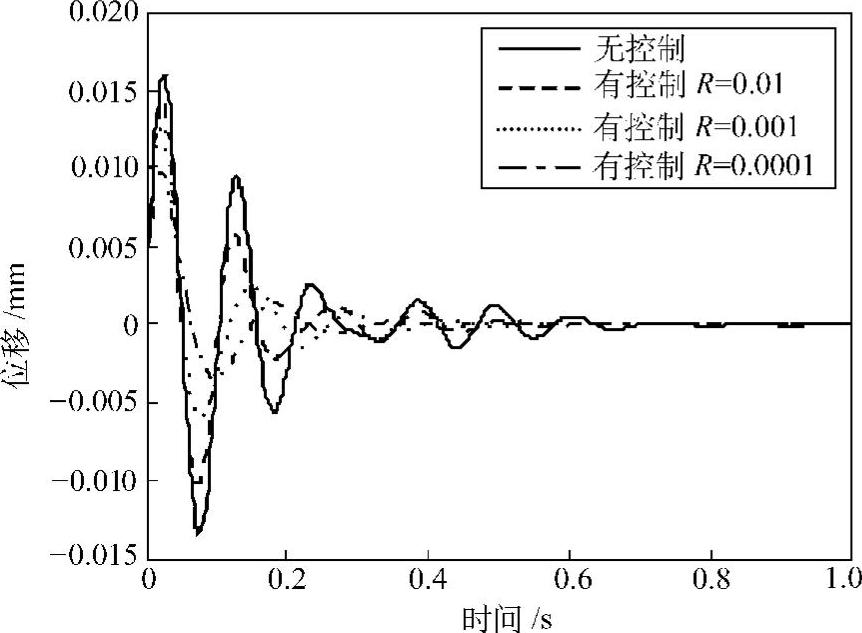
图2.62 主动动力吸振器作用下的主振动系的时间响应

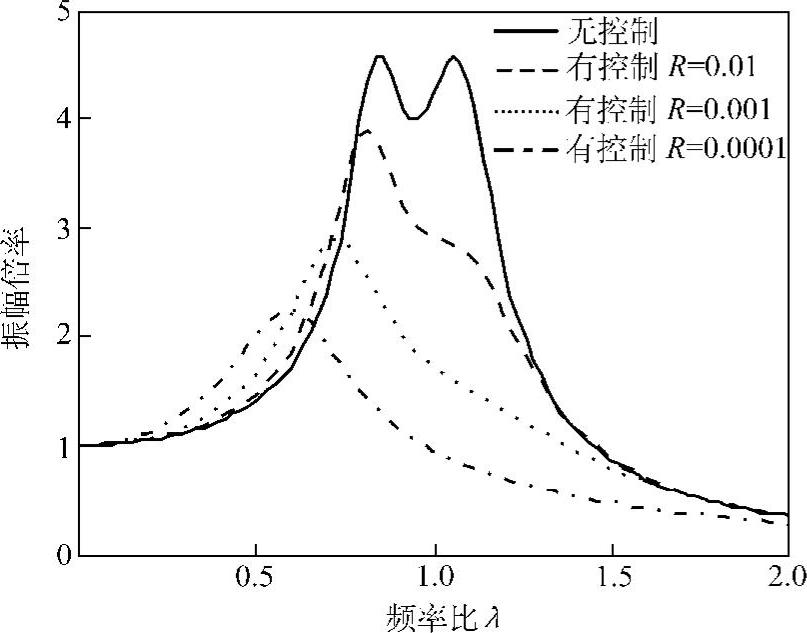
图2.63 主动动力吸振器作用下的主振动系的频率响应

以上介绍的是动力吸振器的主动控制方法。对于实际的主动动力吸振器设计，还应考虑元器件本身的性能及信号检测方法。在实际中，把吸振器与主振动系之间的相对位移作为状态反馈量可能更方便，即

x_d=x₂-x₁

这时，需要对状态方程作相应的变形。但是，控制设计方法是一样的。