单自由度系统振动的主动控制方法

这里，以单自由度系统的振动控制为例，对LQ最优控制的设计过程进行说明。

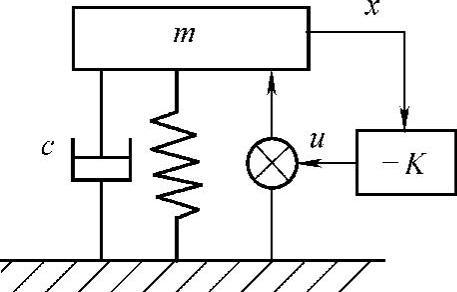
图2.58 基于状态反馈的单自由度振动控制模型

基于状态反馈的单自由度振动控制系统如图2.58所示。同时考虑上外力F（t）与控制力u（t）的运动方程为

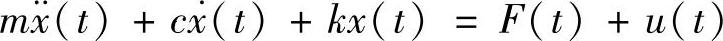
控制力u（t）是由位移、速度、加速度等状态量的反馈构成的，为

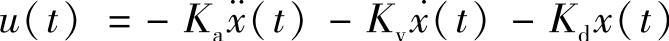
代入运动方程，得

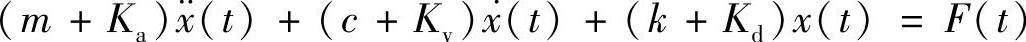
可见，状态反馈控制其实是通过调整原有系统的特性（质量、阻尼、刚性）来抵御外部激励的。因此，在控制系统设计阶段，可以暂不考虑外部激励的影响，而只针对系统本身的特性来进行。这样，仅在控制力作用下的系统的运动方程为

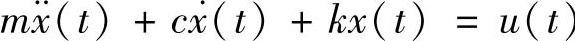
所对应的状态方程为

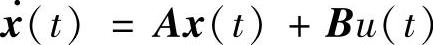
其中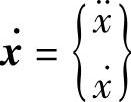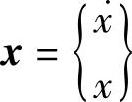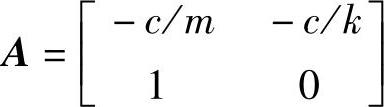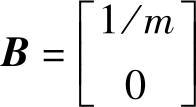，，，，系统的响应方程为

y（t）=Cx（t）(https://www.xing528.com)

选取C=[01]，即可得到位移响应。

根据LQ最优控制理论，控制信号u（t）应使以下二次型评价函数达到最小

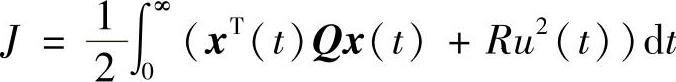
这里取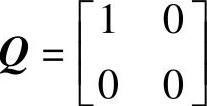，则评价函数变为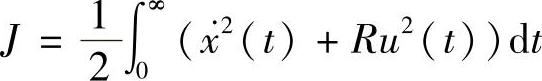。可见，最优控制的目标是使系统的动能最小。由于只有一个控制力，R是一个标量，通过调节它的值，可以改变控制能量的大小以及控制效果。

图2.59是系统的单位脉冲响应，图2.60是系统的频率响应函数。可见，状态反馈控制改善了系统的动态性能。

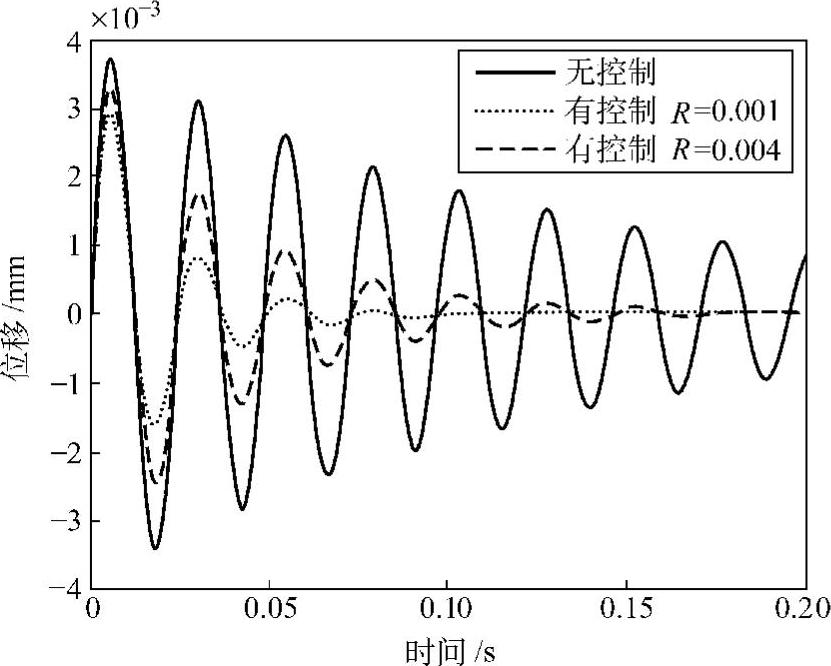
图2.59 单自由度系统的冲击响应函数

当R=0.004时，由式（2.49）求得的最优增益矩阵为K=[11.80.0]；当R=0.001时，求得的最优增益矩阵为K=[27.30.0]。由于对应于位移状态量的增益等于0，控制效果是由速度反馈来增加系统的阻尼而实现的，而且R越小，速度反馈增益越大。

进一步考察可知，如果选取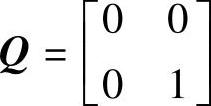，则评价函数变为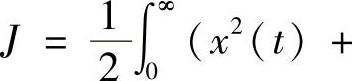Ru²（t））dt，即把系统的弹性势能作为优化目标。这时，要达到同样的控制效果，同时需要速度反馈和位移反馈，而且反馈增益很大，也就是说，所需要的控制能量很大。因此，对于振动控制来说，在选取加权矩阵Q时，最好是把与速度项对应的值选为1，其余选为0。

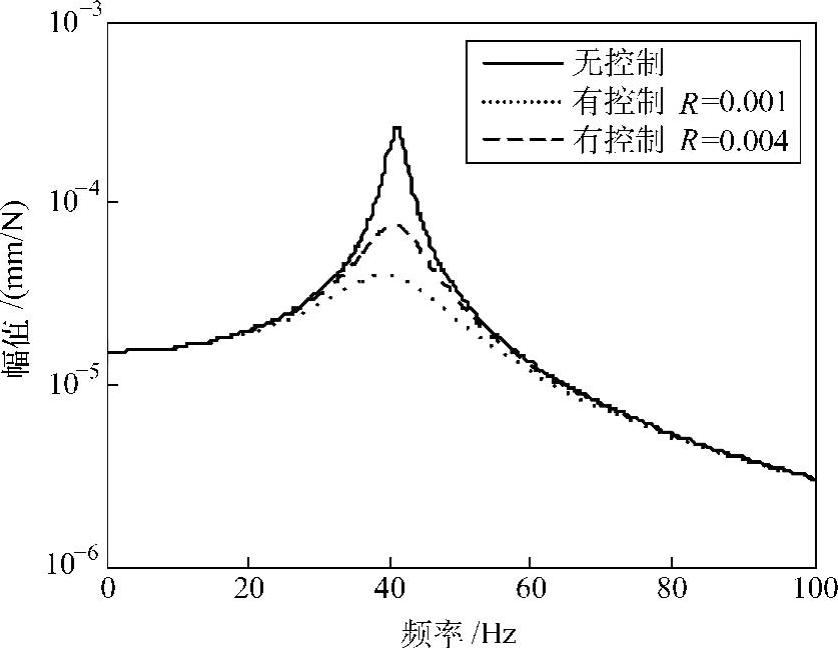
图2.60 单自由度系统的频率响应函数

上述基于LQ最优控制理论的振动控制设计方法，可以很方便地推广到多自由度系统的振动控制中。

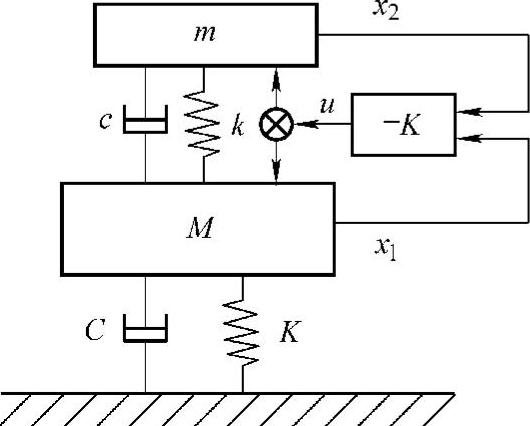
图2.61 主动动力吸振器的二自由度模型