现代控制理论概述

对于多输入多输出系统（Multiple Input Multiple Output，MIMO），应用上述基于传递函数的控制系统设计方法很复杂，基于状态空间的现代控制理论则为这类问题提供了有效的工具。现代控制理论所涉及的内容很多，这里主要介绍振动控制中常用的最优控制理论。

1.状态空间（State-Space）

对于一个单自由度振动系统，运动方程为

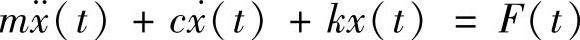
变形为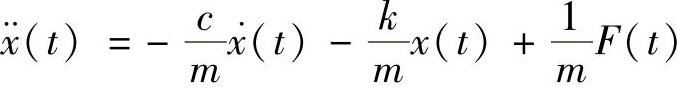

引入等式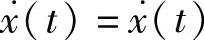

把以上两个方程结合起来，可以写成以下矩阵的形式

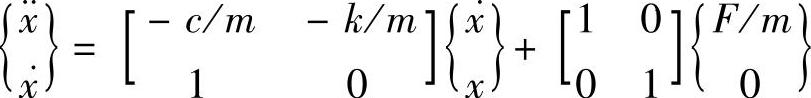
令，，，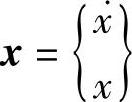

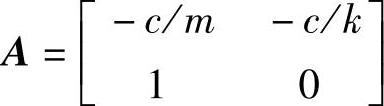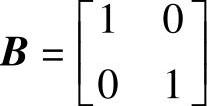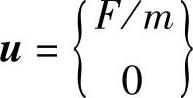
则得

式（2.45）称为状态方程，x为状态向量，A、B为状态矩阵。另外，系统的响应可以用输出向量方程式（2.46）表示

y（t）=Cx（t）+Du（t） （2.46）

C为观测矩阵，通常由1与0组成；D一般为0矩阵。方程式（2.45）和式（2.46）合起来称为线性系统在状态空间上的描述。

以上的状态方程虽然是从单自由度系统出发得到的，但其形式具有普遍性。对于多自由度系统，同样可以用方程式（2.45）和式（2.46）来表述。

2.状态的可控性与可观测性

线性系统的可控性与可观测性是现代控制理论的重要概念。

所谓可控性，是指对于方程式（2.45）所示的系统，如果控制函数u（t）可以把系统的某个状态量从初始值x₀转移到x₁，则称系统的该状态量是可控的。如果每个状态量都可控，则称系统的状态完全可控。可见，状态量可控性反映了系统输入控制其状态的能力。

所谓可观测性，是指对于方程式（2.46）所示的系统响应，如果控制函数u（t）=0，在任意时间段上，对于系统的某个非零初始状态量x₀，响应y（t）≠0，则称这个状态可观测；否则，称为不可观测。如果除了零状态以外没有不可观测的状态，则称系统是完全可观测的。显然，状态量可观测性代表了系统输出反映其状态的能力。

这里以振动控制为例，对可控性与可观测性的物理含义进行说明。如果把激振器安装在振动的节点位置（振幅为0的部位），则控制力无法改变结构的振动状态，即不可控；同样，如果把加速度传感器安装在振动的节点位置，则无法测量到振动的水平，即不可观测。

可控性及可观测性的代数判断准则为：设线性系统的状态矩阵A为n×n的矩阵，B为n×k的矩阵，C为r×n的矩阵，可构成以下新的矩阵

可控制性矩阵：M=[BABA²B…A^n-1B]_n×nk

可观测性矩阵：N=[C^TA^TC^T（A²）T C^T…（A^n-1）^TC^T]_n×nr如果矩阵M的秩（rank）为n，则称系统可控；如果矩阵N的秩为n，则称系统可观测。

3.LQ最优控制理论（Optimal Control）

对于方程式（2.45）所代表的线性系统来说，最优控制问题是使以下二次型评价函数达到最小（Least Quadratic Cost Function）。(www.xing528.com)

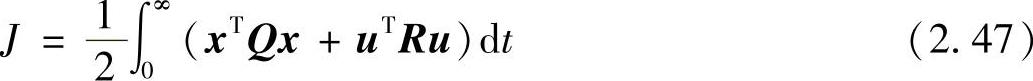
其中，Q、R是系数矩阵。如果Q为半正定矩阵、R为正定矩阵，且已知系统是可控的，则最优控制向量由以下状态反馈来决定

u（t）=-Kx（t） （2.48）

其中增益矩阵K由式（2.49）决定

K=R^-1B^TP （2.49）

这里，P为下列Riccati方程的对称正定解

A^TP+PA-PBR^-1B^TP+Q=0 （2.50）

将式（2.48）代入式（2.45），可得闭环系统的状态方程为

该方程的解为

x₀为初始状态量。闭环系统的特征方程为A-KB=0，其根就是特征值。若所有特征值均具有负实部，则闭环系统稳定。

最优控制的关键是状态反馈。可以证明，只要系统可控且可观测，则可以通过状态反馈任意改变系统的特征值；即使原有系统的特征值具有正实部，即不稳定，也可以通过适当的反馈增益矩阵K使新系统变得稳定。图2.57是引入状态反馈的控制系统的流程图。

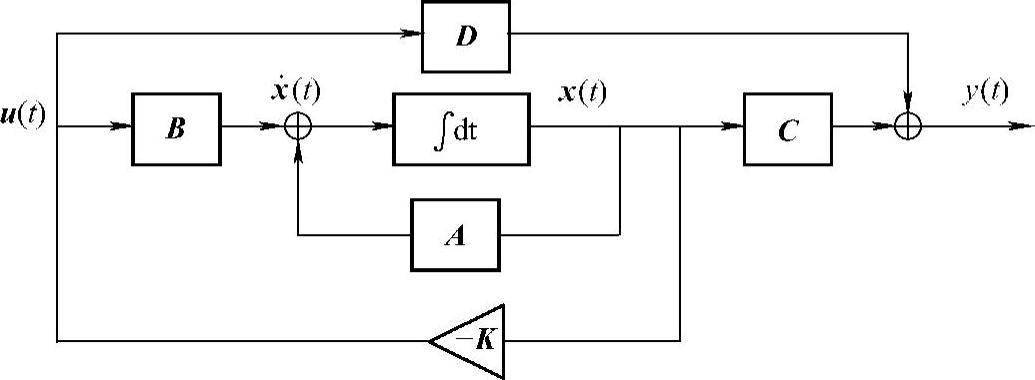
图2.57 状态空间的控制系统

以上就是LQ最优控制理论的基本框架。本来求解Riccati方程不容易，但现在借助于Matlab可以方便地得到它的解。对于振动控制来说，评价函数（2.47）的物理含义可以理解为使得振动能量（第一项）最小的同时，使控制能量（第二项）也要最小。遗憾的是，关于系数矩阵Q、R的选取，尚无一个系统的方法，现在主要是利用计算机仿真进行调整。一般地，R的值越小，控制的效果越好，但耗能也越大。

4.准最优控制理论（Sub-optimal Control）

LQ最优控制理论的前提是建立在所有状态量的反馈基础之上的。也就是说，要获得最优控制效果，必须测量到所有的状态量并反馈回去。对于实际的控制系统设计来说，这是一个苛刻的条件。由于传感器设置场所的限制以及成本问题，可能无法或者没有必要获得所有状态量的信息。在这种情况下，可以应用准最优控制理论代替LQ最优控制理论。

假设可以测量到的状态量为z=Sx，S为由0和1构成的变换矩阵，则可以构成以下状态反馈

u（t）=-K_sz（t） （2.53）

K_s为准最优控制的反馈增益矩阵。严密求解K_s很复杂，通常利用最小范数的方法决定K_s，即寻找K_s使它与LQ最优控制的增益矩阵K的差‖K_s-K‖最小。其结果为

K_s=KS^T（SS^T）-1 S （2.54）

这个结果相当于把LQ最优控制的增益矩阵中与测量不到的状态量所对应的值去掉而已。所以，其设计过程仍然是先根据LQ最优控制理论求得K，再通过式（2.54）的变换得到K_s。

这样，虽然可以很方便地处理状态量测量不全的问题，由式（2.54）决定的部分状态反馈并不能像完全状态反馈那样保证系统的稳定性。所以，在实际应用中应加以注意。一般情况下，应用由式（2.54）决定的准最优控制不会有大的问题。