古典控制理论的应用和特点

最初的控制设计主要是针对只有一个输入一个输出的系统（Single Input Single Output，SISO）。对于这样的系统，利用传递函数（输出信号与输入信号之比）可以方便地表述系统的特征。这种基于传递函数的针对单输入单输出系统的控制设计方法称为古典控制理论。

图2.35所示为古典控制系统的设计概念图。图2.35a为原有的单输入单输出系统，尚不存在控制的问题。图2.35b引入反馈环节，从而构成了一个反馈控制系统，即引入偏差信号e（t）=u（t）-x（t），把它作为控制输入对系统进行干预，目标是使偏差信号为零。这是控制系统的最基本构成。通常，为了提高和保证控制系统的各种性能，还需要引入校正环节或称补偿环节，如图2.35c所示。常用的有串联校正和反馈校正，后者也称并联校正。事实上，控制系统的设计很大程度上就是指校正器的设计。

上述控制系统的功能实际上是保证输出信号对输入信号的追踪性能。这里，输入信号可以理解为目标信号或指令信号，控制的结果就是要使输出信号尽量接近目标信号。例如将火箭的设计运行轨迹（位置随时间变化的函数）作为输入，输出就是实际的运行轨迹。显然，对火箭的控制就是要使实际的运行轨迹无限地接近设计轨迹，这就对控制系统提出了稳、准、快的要求。在此，我们先对线性系统的特征做一下介绍，然后结合一个事例，对古典控制的设计方法做一个简要说明。

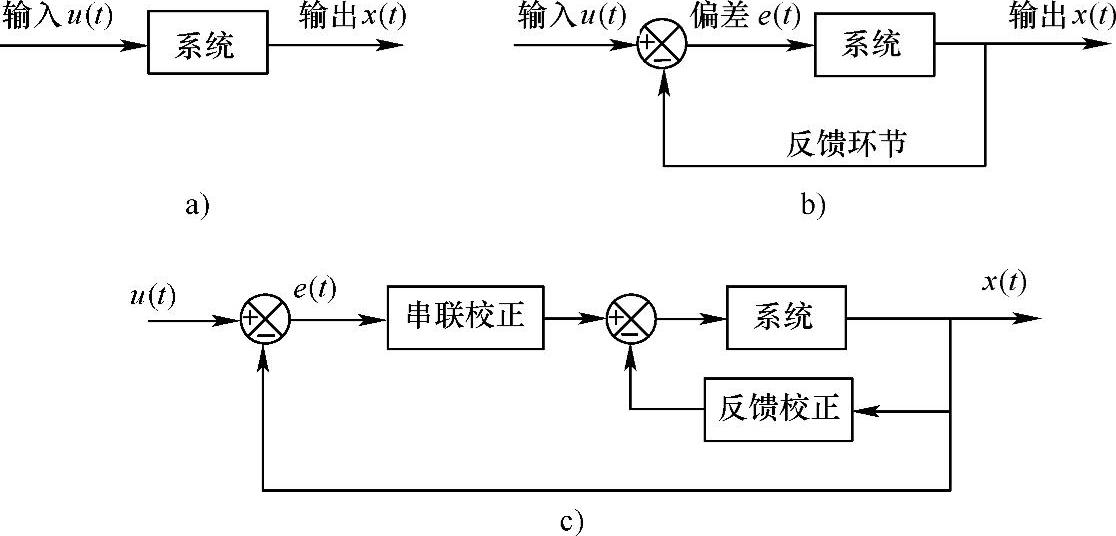
图2.35 反馈控制系统的概念图

a）单输入单输出系统 b）引入反馈环节的控制系统 c）引入校正环节的控制系统

1.线性系统的传递函数

一般的线性系统可以用微分方程式（2.34）来描述

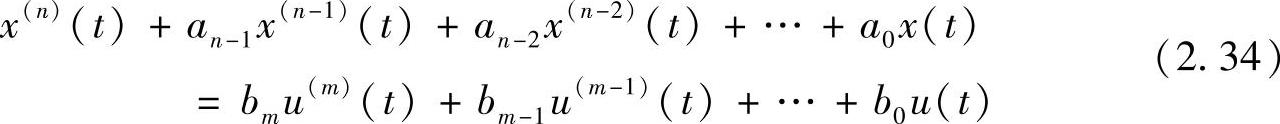
方程式（2.34）左边代表系统的响应输出，右边表示外部输入，上标代表微分次数。单自由度振动系统的运动方程式（1.2）就是一个简单的例子。在系统参数（上式中的各个系数）未知的情况下，可以用单位脉冲函数激励系统，得到系统的冲击响应函数g（t），再由卷积公式求得在任意外部激励下的响应（参见1.6节的描述）为

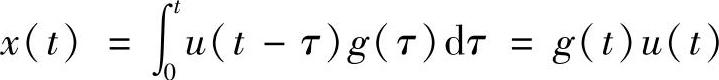
由于卷积运算很不方便，因此通常运用1.6.3节所介绍的拉氏变换把时域信号转换为拉氏域信号进行处理，然后应用拉氏逆变换求得时域响应。假定初始条件为0，式（2.34）的拉氏变换为

即输出信号的拉氏变换与输入信号的拉氏变换之间有以下关系

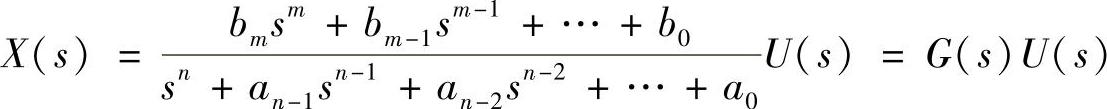
其中，G（s）为系统的传递函数（冲击响应的拉氏变换），反映系统的内在特征。

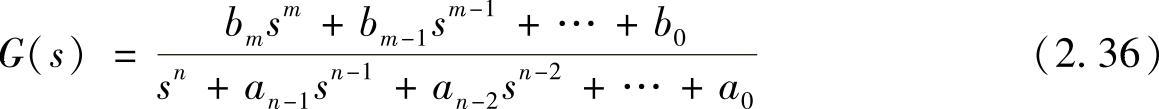
这样，时域中的输入/输出信号的复杂关系变换为拉氏域的简单的乘积关系（见图2.36）。这个特点给利用方块图来图解表示系统的功能及信号流程带来了极大方便。图2.37所示为几个简单的方块图及其简化。

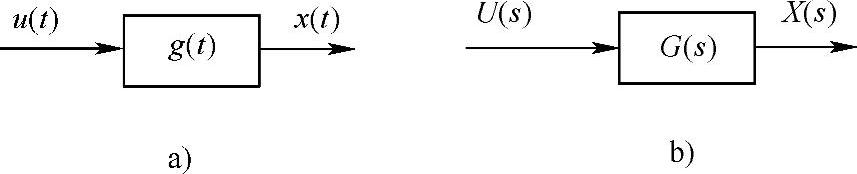
图2.36 控制系统信号流程

a）时域：x（t）=g（t）∗u（t） b）拉氏域：X（t）=G（t）U（t）

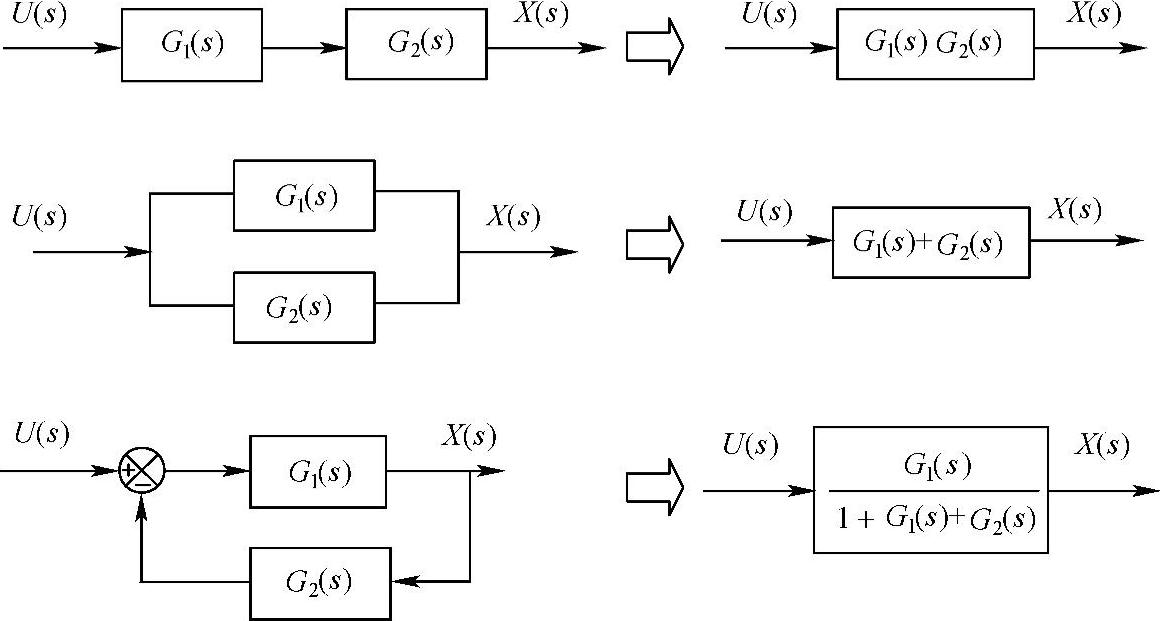
图2.37 传递函数的方块图及其简化

2.线性系统的稳定性

我们先来考察一个质量为m的刚体运动控制的简单例子。图2.38所示为该控制系统的示意图。其中，刚体的特性用传递函数G₀（s）=1/m表示，驱动装置的特性由一阶惯性环节1/（Ts+1）来表示（T为常数）。输入信号为目标速度，反馈信号为刚体的速度。这是一个最基本的反馈控制系统，K为控制增益，相当于一个简单的串联校正环节。其控制过程是：偏差信号输入到驱动装置（马达），产生的驱动力作用在刚体上，使刚体产生加速度（a=F/m）；对该加速度积分一次，即得

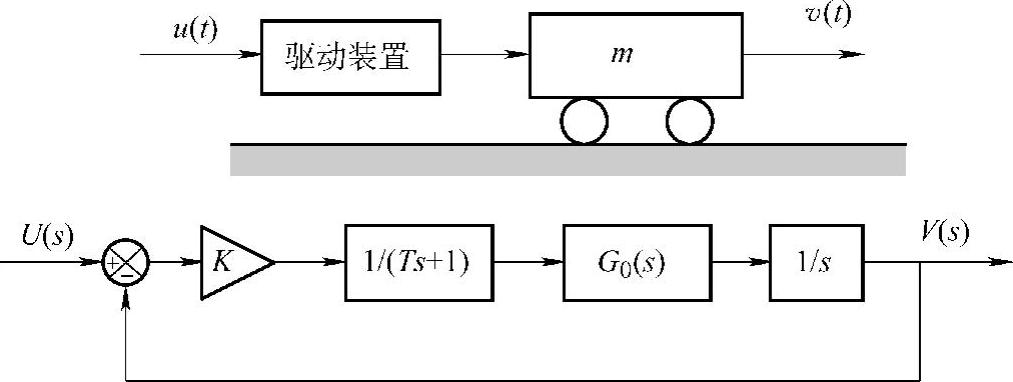
图2.38 刚体运动控制的简单例子

到刚体的速度，然后把该速度信号反馈回去，与目标信号进行比较。

图2.39为速度反馈控制的结果，其中，细线表示目标速度。当控制增益K=1时，刚体的速度远跟随不上目标速度；当控制增益K=10时，刚体的速度基本可以跟随上目标速度；当控制增益K=50时，刚体的速度很快可以跟随上目标速度，但有一点过冲。可见，随着增益的增加，系统响应的快速性得以提高。这里有一个前提条件，就是这个控制系统是稳定的。

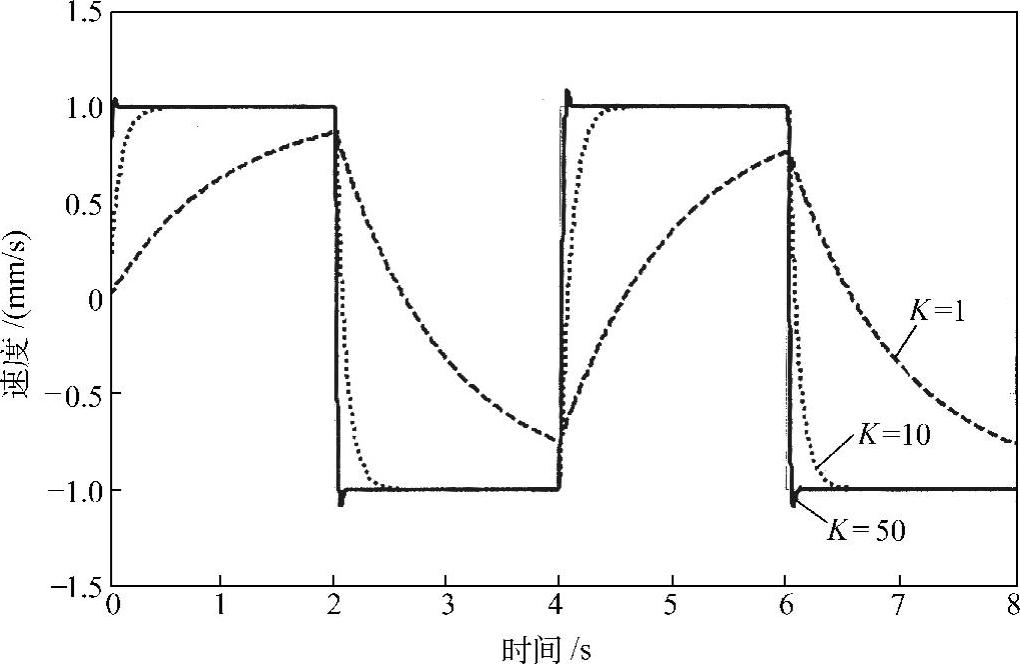
图2.39 速度反馈控制的结果（m=1，T=0.01，细线为目标速度）

同样是如图2.38所示的刚体运动的情况，如果假定目标信号不是速度，而是位移，则控制系统变为如图2.40所示的位移反馈控制，图2.41是控制结果。这时，输出信号不但无法跟踪输入信号，而且随着增益的增加，越发呈现发散的趋势。这样的控制系统称为不稳定系统。对于不稳定系统，讨论快速性和精度已无意义。

图2.40 刚体运动的位移反馈控制

由以上例子可见，引入反馈控制之后，可能会引起系统的不稳定性。关于系统的静态稳定性和动态稳定性问题，我们在自激振动一节（1.7.1）中已有所介绍。这里进一步来探讨控制系统的稳定性问题。

稳定性是系统内在的性质，从本质上来说，与外界干扰无关。只是在外界激励下，不稳定系统通过发散现象，把其不稳定的性质暴露出来。显然，重要的是在激励系统之前，应该对其稳定性有所把握，否则可能会造成无法挽回的破坏或损失。既然稳定性与外界激励无关，我们可以令方程式（2.34）的右边为0，从而得到描述系统特征的线性齐次方程式（2.37）

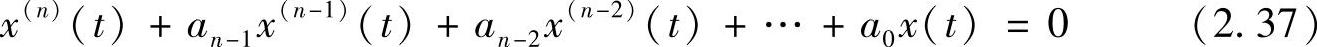
这个方程反映了包括控制环节在内的整个系统的内在特征。根据线性微分方程的解法（参见1.2节定理1），若能找到方程式（2.37）的所有特解，则通解为这些特解的线性组合。这里，令x=e^λt，λ为常数，代入以上方程，可得

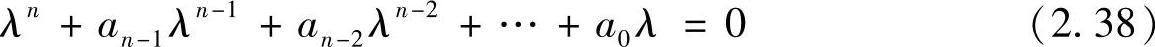
这是一个n次代数方程，有n个根，对应于方程式（2.37）的n个特解e^λ1t、e^λ2t、…、e^λnt。因此，方程式（2.37）的通解可以表示为

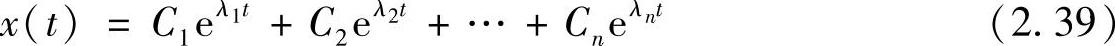
其中，C₁、…、C_n为常数。我们把λ称为系统的特征值。

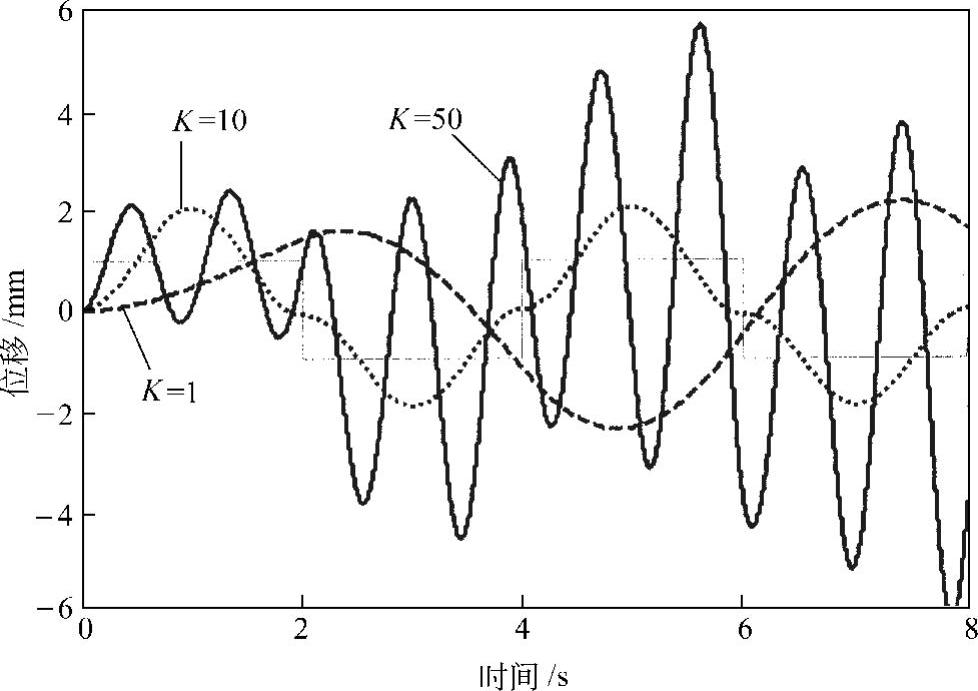
图2.41 位移反馈控制的结果（m=1，T=0.01，细线为目标位移）

一般来说，方程式（2.38）的根（特征值）为复数，即λ_i=α_i+jβ_i（i=1～n）。显然，如果有一个根的实部大于0，则随着时间的增加，式（2.39）所示的响应的振幅会越来越大，也就是说，系统趋于发散。只有当所有根的实部小于0时，式（2.39）所示的响应才会收敛。因此，控制系统稳定性的条件是：系统特征值的实部小于0。

观察式（2.36）和式（2.38）可见，式（2.38）左边与式（2.36）的分母形式完全相同。因此，直接令传递函数G（s）的分母为0，即可求得系统的特征值。这里，s=λ。

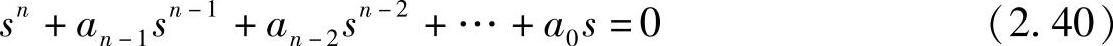
式（2.40）为控制系统的特征方程。例如对于如图2.38所示的控制系统，系统的传递函数为

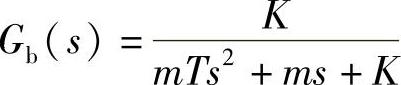
特征方程为

mTs²+ms+K=0

取m=1，T=0.01。在K=10时，根为s₁=-88.73，s₂=-11.27；在K=50时，根为s₁=-50.00+j50.00，s₂=-50.00-j50.00。两个根都具有负实部，因此系统稳定。而对于如图2.40所示的控制系统，系统的传递函数为

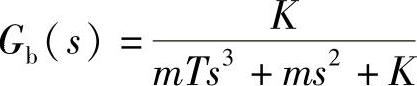
特征方程为

mTs³+ms²+K=0

此时，K=10时，根为s₁=-100.1，s₂=0.05+j3.16，s₃=0.05-j3.16；K=50时，根为s₁=-100.5，s₂=0.25+j7.05，s₃=0.25-j7.05。有两个根的实部为正，因此该系统不稳定。

这里需要指出，上述控制系统的传递函数G_b（s）称为系统的闭环传递函数，代表的是输入信号与输出信号之间的关系。另外，我们把偏差信号与反馈信号之间的传递函数称为系统的开环传递函数。二者的关系如图2.42所示。对于该图所示的控制系统，其特征方程由闭环传递函数的分母为零得到

1+G₀（s）H（s）=0 （2.41）

显然，特征方程的根就是闭环传递函数的极点。另一方面，分子G₀（s）=0的根为闭环传递函数的零点。如果存在实部为正的极点，则系统不稳定。这时，可以通过调整零点位置，使其与不稳定极点相抵消，从而达到稳定系统的目的。这种方法称为零极点配置法。

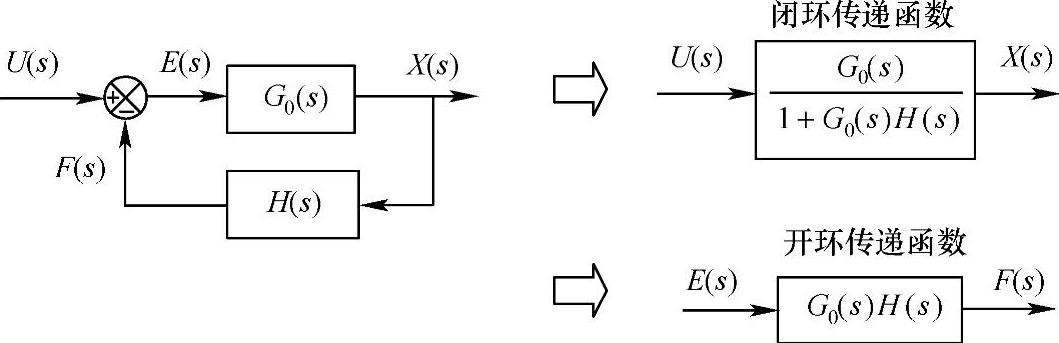
图2.42 闭环传递函数与开环传递函数

工程上判定稳定性的方法常用乃氏图解法。乃氏图是在以横轴为实部，纵轴为虚部所构成的[S]平面上，绘制出的频率从-∞到+∞变化时的传递函数轨迹图（s=jω）。作为判定稳定性的几何方法，乃氏图解法的作图对象是开环传递函数，即图2.42中的G₀（s）H（s）。设开环传递函数有p个极点处于[S]平面的右半边（原点处的极点作为左半平面的极点处理），则稳定性判定准则如下：

① p=0时，当ω从-∞到+∞变化时，开环传递函数的轨迹不包围（-1，j0）点，则闭环系统稳定，反之不稳定。

② p＞0时，当ω从-∞到+∞变化时，开环传递函数的轨迹逆时针包围（-1，j0）点p圈，则闭环系统稳定；若逆时针包围（-1，j0）点不到p圈，或顺时针包围（-1，j0）点，则闭环系统不稳定。

也就是说，通过考察开环传递函数的特性，可以判定闭环系统的稳定性。图2.43为一个二阶振荡环节G_k（s）=K/（s²+2ζω_ns+ω²_n）的乃氏图。曲线与单位圆的交点处的频率ω_c反映系统的快速性，原点与该交点的连线与负实轴的夹角ϕ代表稳定性的相位裕量。增益越大，快速性越好，可是安定裕量却越小。

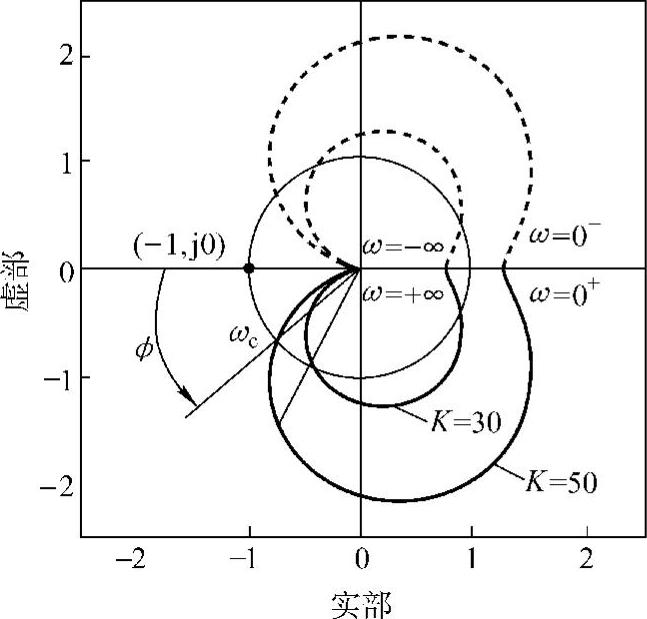
图2.43 一个二阶振荡环节的乃氏图（ω_n=2π，ζ=0.3，K为增益）

此外，利用开环传递函数的伯德图（Bode Plot），即幅频特性曲线和相频特性曲线，也可以判断闭环系统的稳定性。作为举例，图2.44为下记开环传递函数的伯德图。

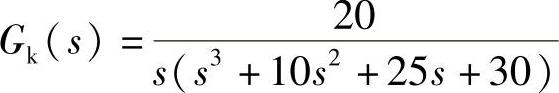
该传递函数在[S]平面右边没有极点。这种情况下，利用伯德图判定稳定性的方法是：幅值为0dB所对应的相位如果越过了-180°线，则闭环系统不稳定；反之稳定。与-180°的距离为相位稳定裕量，例如如果幅值为0dB所对应的相位为-120°，则相位裕量为60°。另一方面，相位-180°所对应的幅值如果大于0dB，则闭环系统不稳定；反之稳定。小于0dB的幅值大小代表幅值稳定裕量，例如如果相位=-180°所对应的幅值为-10dB，则幅值稳定裕量为10dB。一般希望，幅值稳定裕量大于6dB，相位稳定裕量处于30°与60°之间。由此可见，图2.44所示例子的闭环系统为稳定系统。

此外，幅值为0dB所对应的频率称为截止频率，截止频率越高，快速性越好。

3.控制系统的稳态精度

只有对于稳定系统，输出信号才有可能跟踪目标信号。此外，还有一个值得注意的问题就是跟踪的精度问题。我们把输出信号与目标信号的差称为误差。对于不同特点的目标信号，这个误差可能为0，可能不为0，甚至可能无穷大。引起误差的原因可能是元器件本身的缺欠，如摩擦、间隙、零点漂移、老化等，也可能是由于外界干扰。但这些原因都不是这里要讨论的，这里要讨论的误差是指控制系统本身的原理性误差。

以一个单位反馈控制系统为例（见图2.45，非单位反馈可以等价为单位反馈），误差信号为E（s）=U（s）-X（s）=U（s）-E（s）G（s），即

(www.xing528.com)

这里，系统的开环传递函数等于G（s），即G_k（s）=G（s）。利用拉氏变换的终值定理，可以得到当时间无限大时的稳态误差为

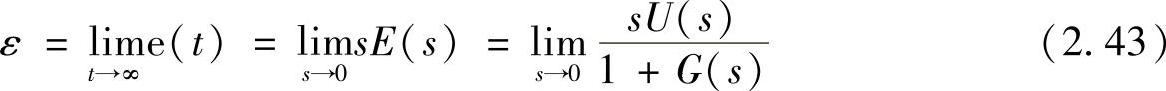
图2.44 开环传递函数的伯德图

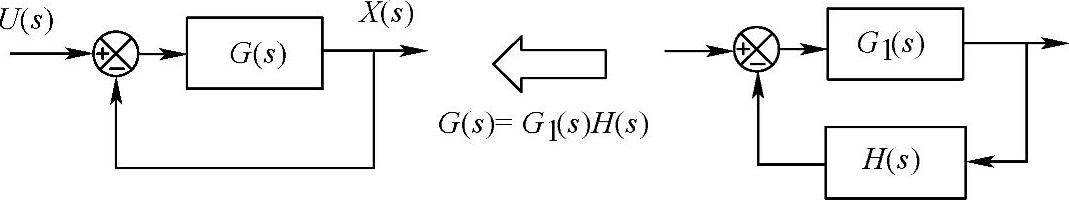
图2.45 单位反馈系统

可见，稳态精度不但与控制系统本身有关，而且与输入有关。通常，利用以下典型输入信号对稳态误差进行考察：

① 单位阶跃输入：u（t）=1，U（s）=1/s。

② 单位斜坡输入（等速输入）：u（t）=t，U（s）=1/s²。

③ 等加速输入：u（t）=t²/2，U（s）=1/s³。

此外，系统开环传递函数可以表示为以下一般形式

其中，K为开环增益，Q（s）、P（s）为s的多项式，分母的阶数高于分子。当r=0时，称为0型系统；当r=1时，称为Ⅰ型系统；当r=2时，称为Ⅱ型系统。把上述典型输入和传递函数公式代入式（2.43），可以求得这些典型情况下的稳态误差，如表2.1所示。

表2.1 典型情况下的稳态误差

可见，单位阶跃输入下，稳态误差最易控制，输入随时间的变化越快，误差越不易控制。例如等加速输入下，不管如何增大增益，对于0型系统和Ⅰ型系统来说，最终的稳态误差为无限大；Ⅱ型以上的高阶系统精度好，但实现起来比较困难。

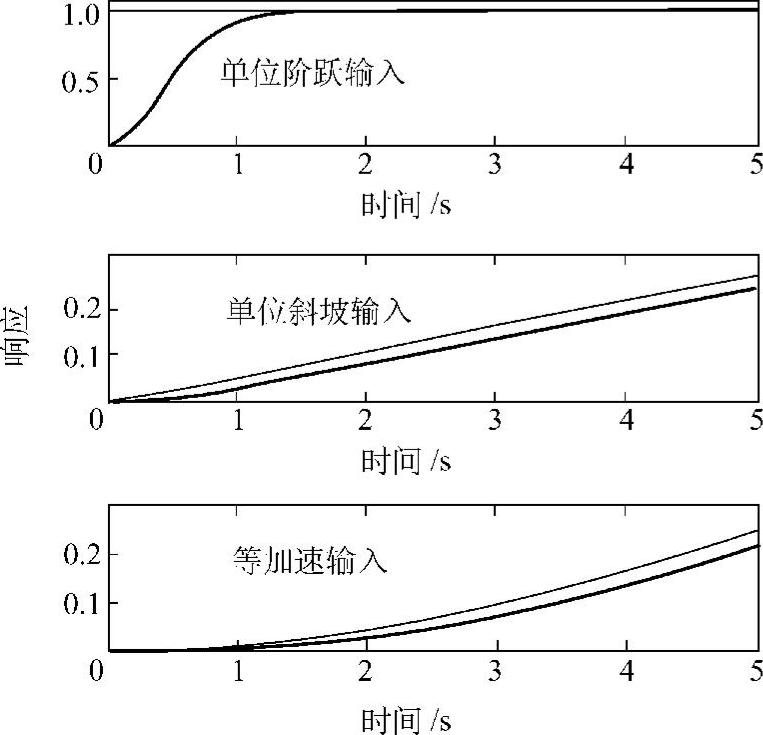
图2.46 Ⅰ型系统在不同输入下的响应（细线：输入；粗线：输出）

图2.46绘出了如图2.47所示的控制系统（后述）的在不同输入信号下的输出响应（计算条件：m=1，T=0.01，K_v=5，K=10）。单位阶跃输入下，输出无限接近于输入，稳态误差为0；单位斜坡输入时，稳态误差为一定；等加速输入时，输出越来越偏离输入，稳态误差为无穷大。可见，图2.47所示的控制系统是一个Ⅰ型系统。

容易理解，在Ⅰ型系统中串入一个积分环节（1/s），可以把系统变为Ⅱ阶系统，从而可以改善稳态精度。但是，这样的方法可能会改变系统的稳定性，从而产生动态性能上的问题。改善稳态精度的实用方法是引入顺馈（Feedforward）补偿环节，这种方法既不影响系统的稳定性，理论上又可以完全消除稳态误差。详细请参阅有关参考书。

4.控制系统的校正

为了改进控制系统的稳定性及精度等性能，往往在原有的反馈控制的基础上需要增加适当的校正环节。例如对于如图2.40所示的不稳定系统，增加一个速度反馈的并联校正环节，变为如图2.47所示的系统。图2.48为控制结果的例子。与以前的结果（见图2.41）相比，系统已变得可控。

此时，系统的闭环传递函数为

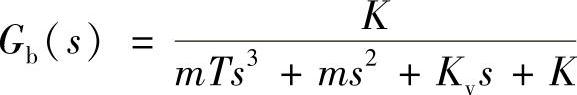
特征方程为

mTs³+ms²+K_vs+K=0

在m=1，T=0.01，K_v=5的条件下，K=10时的根为s₁=-94.84，s₂=-2.58+j1.97，s₃=-2.58-j1.97；K=50时的根为s₁=-95.30，s₂=-2.35+j6.85，s₃=-2.35-j6.85。所有根的实部均为负，因此该系统稳定。

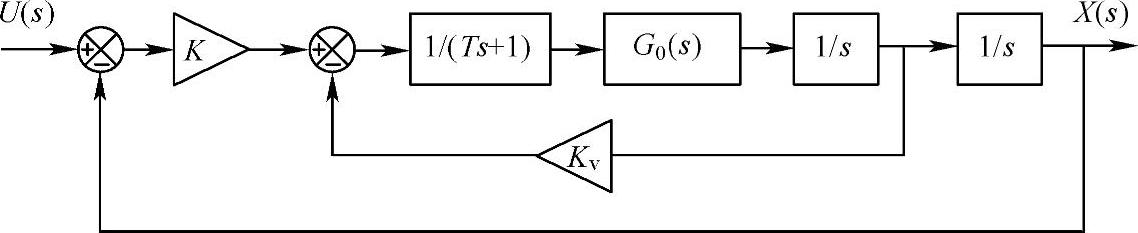
图2.47 增加了并联校正环节的位移反馈控制系统

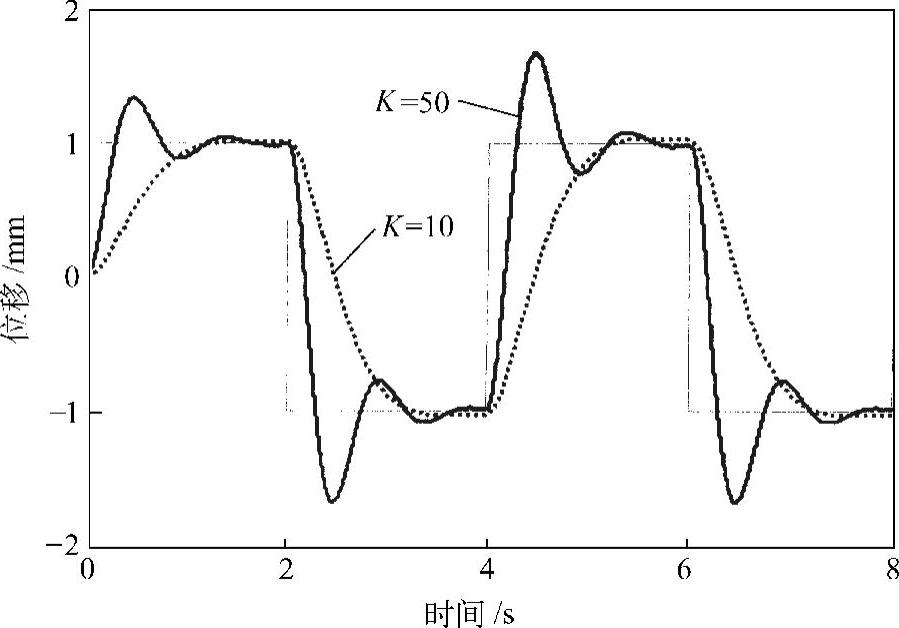
图2.48 增加了校正环节的位移反馈控制的结果（m=1，T=0.01，K_v=5。细线为目标信号）

作为参考，图2.49绘出上述3个控制系统的开环传递函数的乃氏图。实线对应于速度反馈控制的系统（见图2.38），此系统为稳定系统，乃氏曲线不包围点（-1，j0）；点线对应于位移反馈控制系统（见图2.40），此系统为不稳定系统，乃氏曲线包围点（-1，j0）；虚线对应于增加了校正环节的位移反馈控制系统（见图2.47），在K=50的情况下系统稳定，乃氏曲线不包围点（-1，j0）。

另外，图2.50为位移反馈控制系统（实线）及增加了校正环节的系统（点线）的开环传递函数的伯德图。原有系统的相位裕量为负，因此闭环系统不稳定；增加了校正环节的系统相当于相位超前校正，把相位裕量变为正，使得系统变得稳定。但是，当增益过大时，系统再次变为不稳定系统（见图2.51），这种系统称为条件稳定系统。可以利用根轨迹法考察增益由0到∞变化时的闭环系统特征根在[S]平面上的移动轨迹，从而确定保证系统稳定的增益范围。

以上介绍的有关刚体运动控制的例子的传递函数及特点归纳于表2.2中。

表2.2 关于刚体运动控制的三种控制系统的归纳

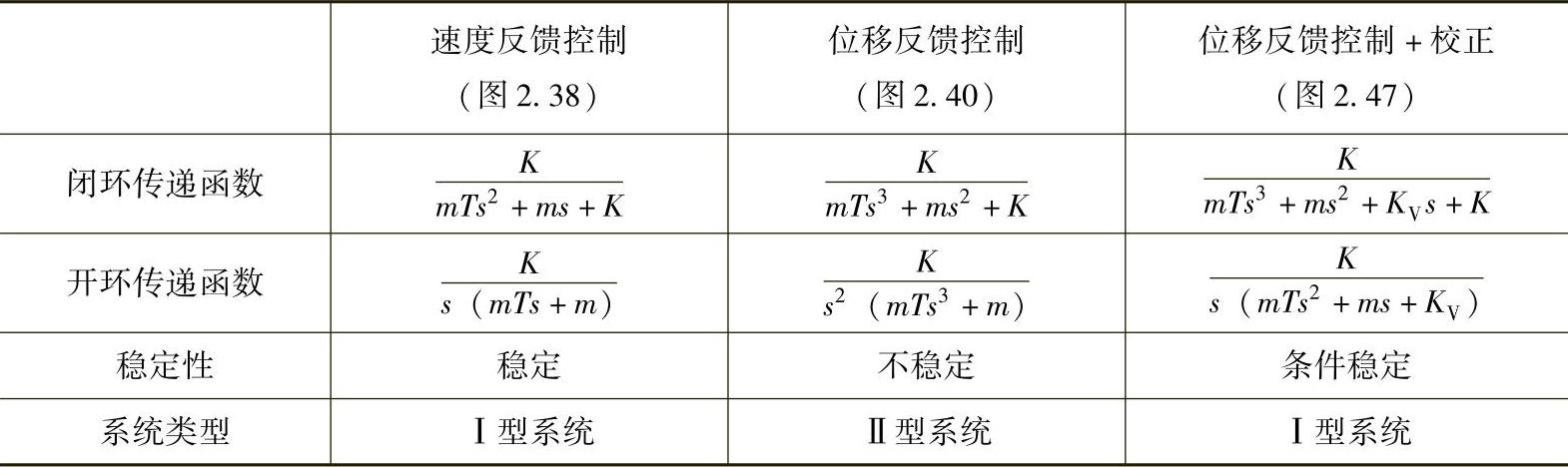
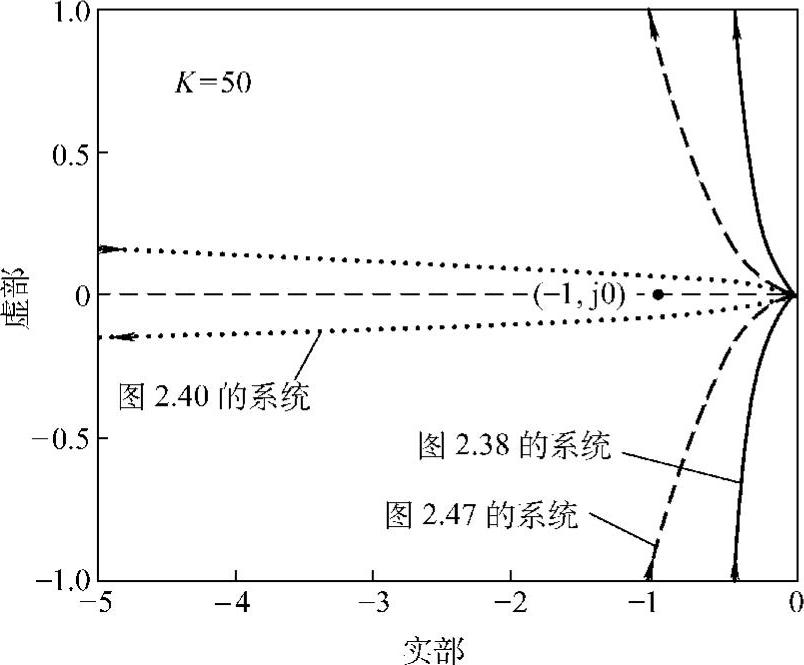
图2.49 三个控制系统的开环传递函数的乃氏图

图2.50 开环传递函数的伯德图（增益K=50）

实线：位移反馈控制系统（见图2.40）

点线：增加了校正环节的系统（见图2.47）

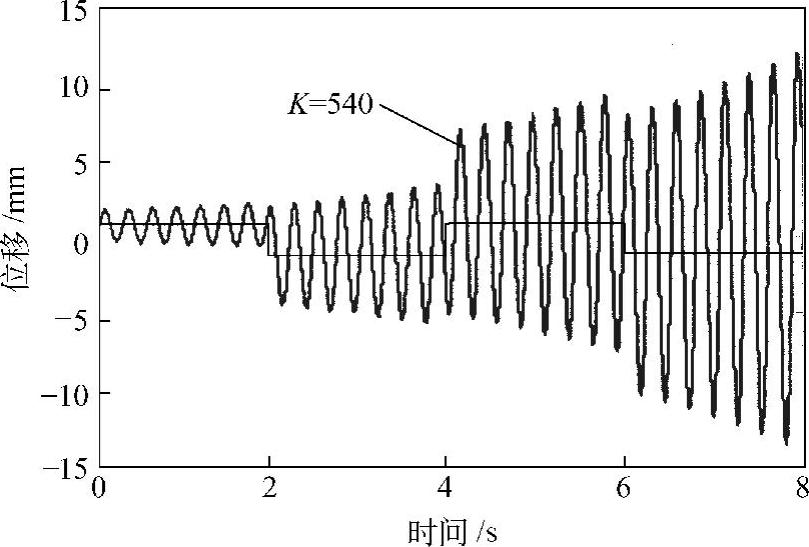
图2.51 增加了校正环节的位移反馈控制的结果（增益过大的情况）

图2.47所示的并联校正环节实际上是通过速度反馈给原有系统引入了阻尼，这种反馈校正在振动控制中尤为重要。

应该说明的是，反馈校正是在原有的主反馈回路上增加新的反馈环节，可以是局部的，也可以是整体的。对于后者，相当于与主反馈环节并联了一个环节，可以用图2.52b进行等价。

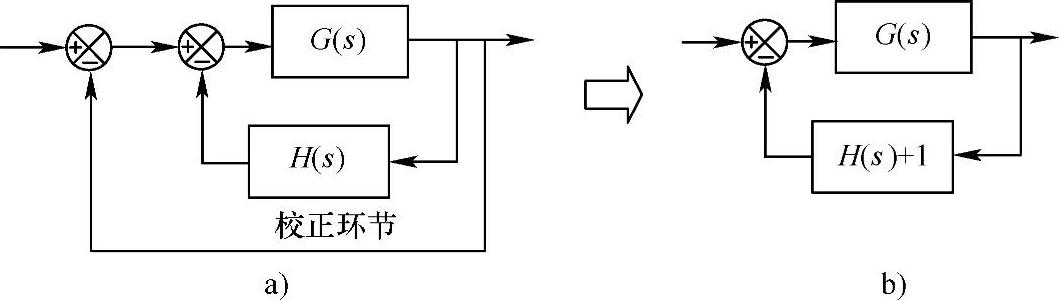
图2.52 反馈校正

a）校正环节与主反馈回路并联的系统 b）等价系统

除了反馈校正外，工程上常用的校正方法有超前校正与滞后校正。它们都属于串联校正，如图2.53所示。

超前校正与滞后校正环节的特性可用以下传递函数表示，其频率特性如图2.54所示。

超前校正：，0＜α＜1

滞后校正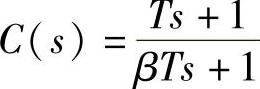：，β＞1

图2.53 串联校正

图2.55为超前校正与滞后校正的作用原理示意图。其中，细线为原有控制系统的开环传递函数。根据伯德图的稳定性判别法则可知，闭环系统不稳定。图2.55a中的粗线为采用超前校正环节后的控制系统的开环传递函数。可见，超前校正环节的作用是把截止频率附近的相位向上移动，并使新的截止频率向高频方向移动，这样不但保证了校正后的系统有充足的稳定裕量，而且提高了系统的快速性。与之相对照，图2.55b中粗线所示的滞后校正环节的作用则是加大增益的下降坡度（即从原有的每倍频程降20dB变为降40dB。相对而言，相当于提高了低频增益），使其与0dB的交点（截止频率）向低频方向移动，从而保证充足的稳定裕量。因此，滞后校正并不是利用相位滞后作用来改善原系统的稳定性，而是利用幅值衰减作用使系统稳定的。滞后校正虽然可以改善系统的稳态误差，但却降低了系统的快速性。

对于振动控制来说，增加结构的阻尼是主要目的。我们知道，阻尼力的相位比位移超前90°，所以，相对于滞后校正，超前校正更适合于振动控制。

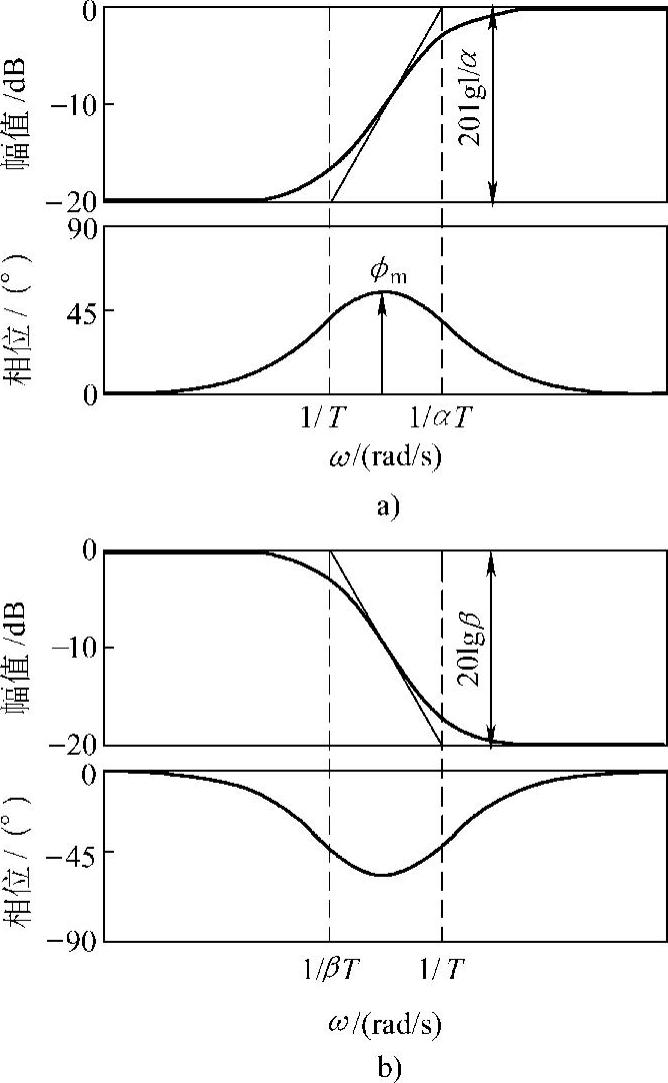
图2.54 超前校正与滞后校正的频率特性（这里取α=0.1，β=10）

a）超前校正 b）滞后校正

超前校正的设计步骤是：首先，确认现有系统的相位裕量，根据目标相位裕量为40°～60°的要求，决定相位超前的最大值Φ_m，进而决定参数α；然后，再由最大相位角所对应的频率ω_m决定参数T。具体的关系式如下：

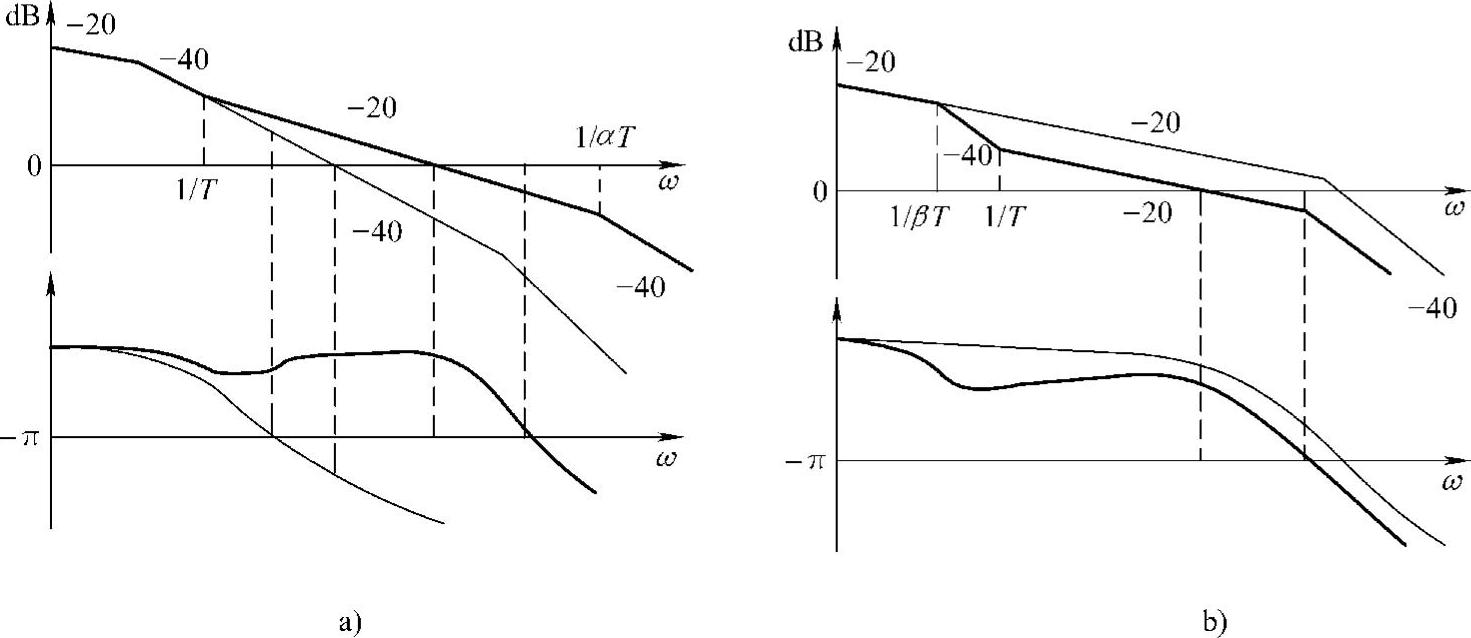
图2.55 超前校正与滞后校正的作用

a）超前校正 b）滞后校正

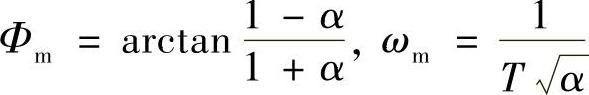
在工程上，经常用比例放大器（Proportional）、积分器（Integral）和微分器（Differential）来构成PI校正、PD校正或PID校正。

PI校正：C（s）=K_p+1/（K_is）

PD校正：C（s）=K_p+K_ds

PID校正：C（s）=K_p+K_ds+1/（K_is）

PD相当于超前校正，PI相当于滞后校正，PID相当于超前-滞后校正。由于PID校正应用得相当普遍，因此古典控制也称PID控制。

对于如图2.38所示的刚体运动控制，引入适当的校正环节，可以构成如图2.56所示的较为实际的控制系统。其中，速度反馈校正环节起到增加阻尼，改善系统动态性能的作用；PI校正环节起到改善稳态精度的作用。

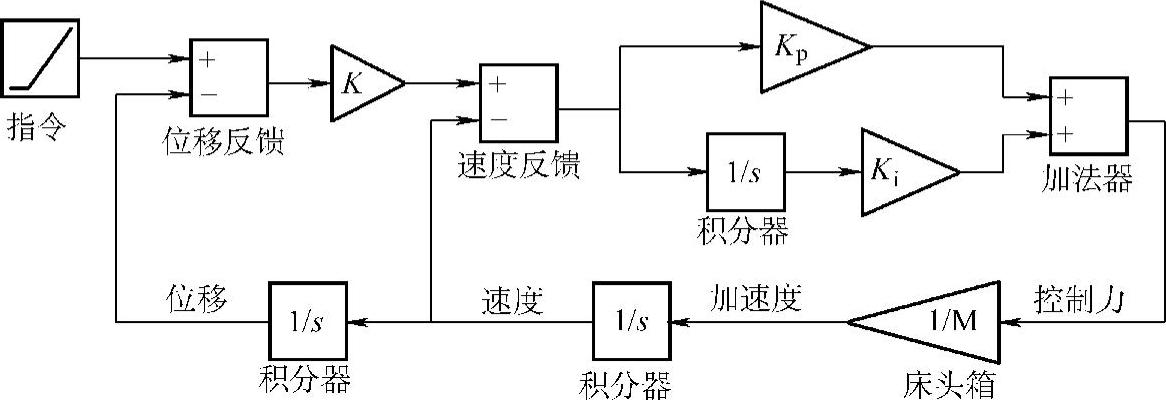
图2.56 刚体运动控制的校正系统