其他形式的吸振器设计与优化

图2.13所示的动力吸振器模型是最常用的形式，本节介绍几种其他形式的吸振器。

1.阻尼接地的形式

动力吸振器的常用形式是阻尼器处于吸振器与被控制的主振动系之间，但在某些情况下，将阻尼器接地（与第3结构相接）则会带来应用上的方便。这种阻尼接地的形式的制振效果比传统形式更加有效。图2.20是这种动力吸振器的示意图。

应用定点理论，可以推导出这种动力吸振器的最优设计原则为

最优同调：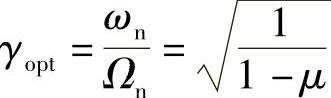

最优阻尼：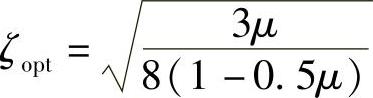

最大振幅倍率：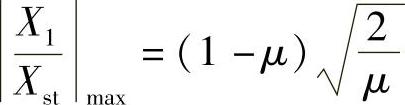

对于同样的质量比，考察最优状态下的制振效果，即比较最大振幅倍率，可以发现：阻尼接地的动力吸振器的制振效果比传统形式的要好。例如在μ=0.1时，可提高减振效果1.1dB；在μ=0.2时，可提高减振效果2.4dB。不增加附加质量而提高减振效果，这是一个有魅力的特点。

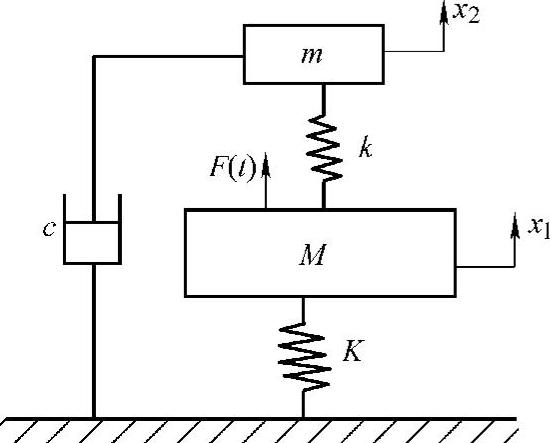
图2.20 阻尼接地形式的动力吸振器

2.多重动力吸振器

把一个动力吸振器的质量一分为二、一分为四等，可以构成多重动力吸振器。这样，总的附加质量没有增加，却有提高控制效果的好处。图2.21所示是一个二重动力吸振器的模型，其最优设计准则为最优同调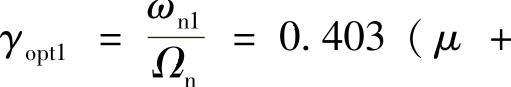：0.13）^-0.434，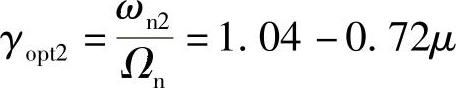

最优阻尼：ζ_opt1=（0.0568μ）^0.285-0.065，ζ_opt2=（0.327μ）^0.377-0.062

最大振幅倍率：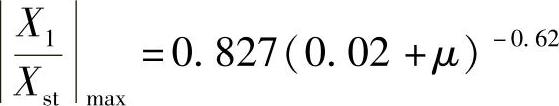

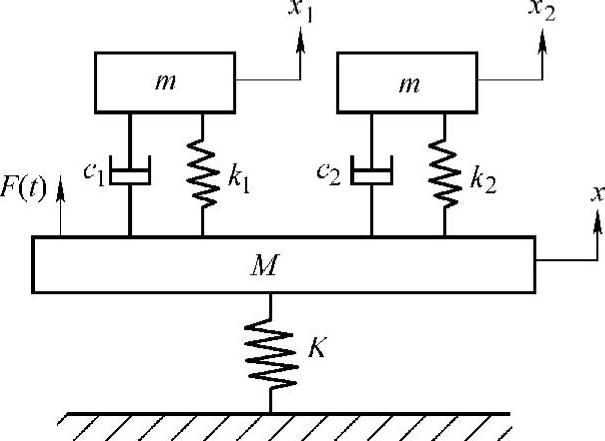
图2.21 二重动力吸振器的模型（质量比μ=m/M）

图2.22是单个动力吸振器与二重动力吸振器的控制效果的比较。可见，在总的附加质量不变的情况下，二重动力吸振器的控制效果要更好。此外，在实际应用中，二重动力吸振器也很容易在构造上实现。图2.23所示为利用板簧设计的二重动力吸振器的示意图。调节板簧的长度和粘弹性材料的厚度，可以实现最优设计。

3.Houde阻尼器

图2.13所示动力吸振器是由质量-弹簧-阻尼所组成的振动子系统，通过调节其固有频率和阻尼，来达到抑制主振动系共振振幅的目的。它只有在最优同调频率上才有较好的制振效果。如果去掉弹簧，只剩下阻尼器，则变为如图2.24所示的吸振器模型，称为Houde阻尼器。这时，不存在同调频率问题，可以在大范围内获得阻尼效果。

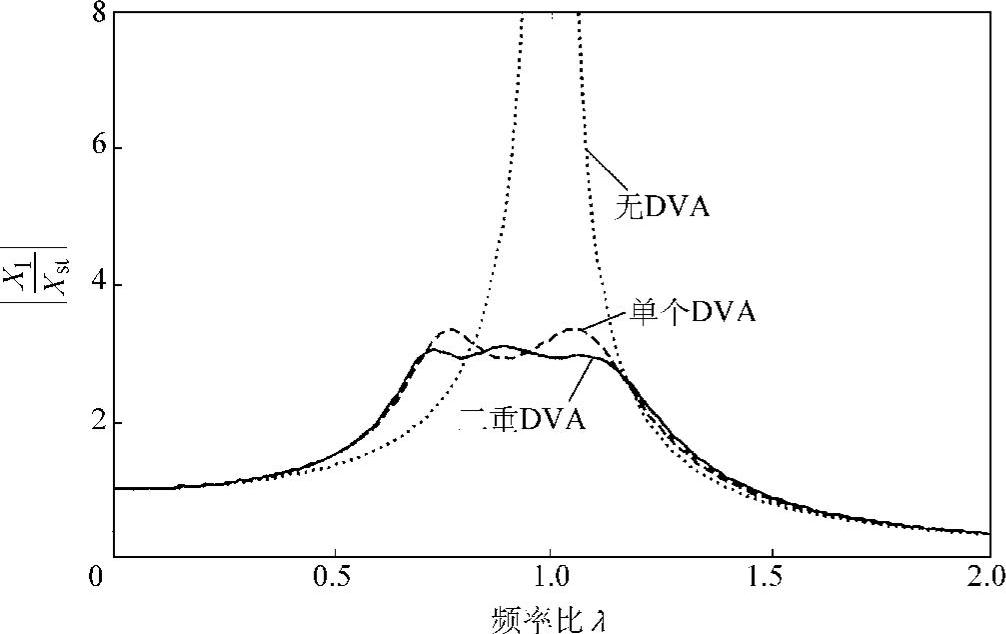
图2.22 单个动力吸振器（μ=0.2）与二重动力吸振器（μ=0.1）的比较

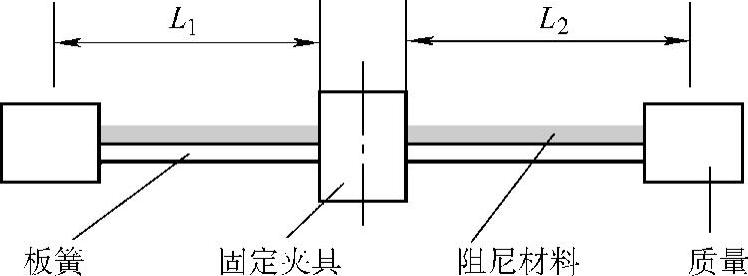
图2.23 利用板簧设计的二重动力吸振器的示意图

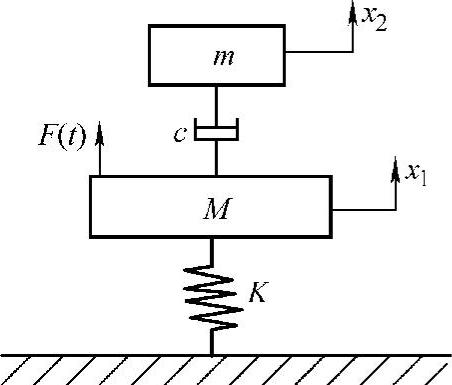
图2.24 Houde阻尼器的模型

考察图2.24系统的振动，主振动系的振幅倍率为

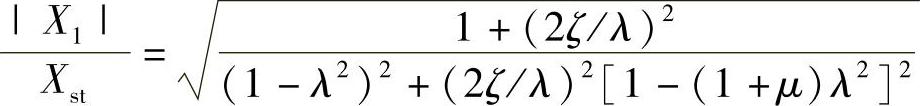
这里，定义阻尼比为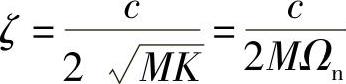。图2.25是根据上式绘制出的不同阻尼比的振幅倍率曲线。由图可见，曲线上存在一个不随阻尼变化的定点，其位置可由ζ=0和ζ=∞两个特殊情况下的振幅确定下来，为

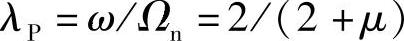
这个定点上的振幅倍率为

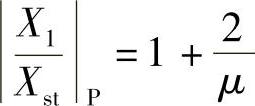
利用同样的方法，可以确定出使得定点成为曲线最大点的最优阻尼为

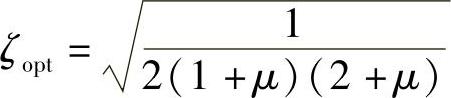
与通常的动力吸振器相比，要达到同样的制振效果，Houde阻尼器需要的附加质量比较大，这就要求在主振动系上有确保安装较大质量的空间。Houde阻尼器最典型的应用是控制轴的扭转振动，如图2.26所示。壳体与轴固结，从而一起旋转，附加质量（惯性圆盘）通过轴承与轴相连，因而可以自由转动。在圆盘与壳体的缝隙中充满了粘性介质——油。当轴发生扭转振动时，圆盘与壳体的相对转动导致粘性阻尼发生，从而起到抑制扭转振动的目的。这样的构造容易获得较大的附加质量。

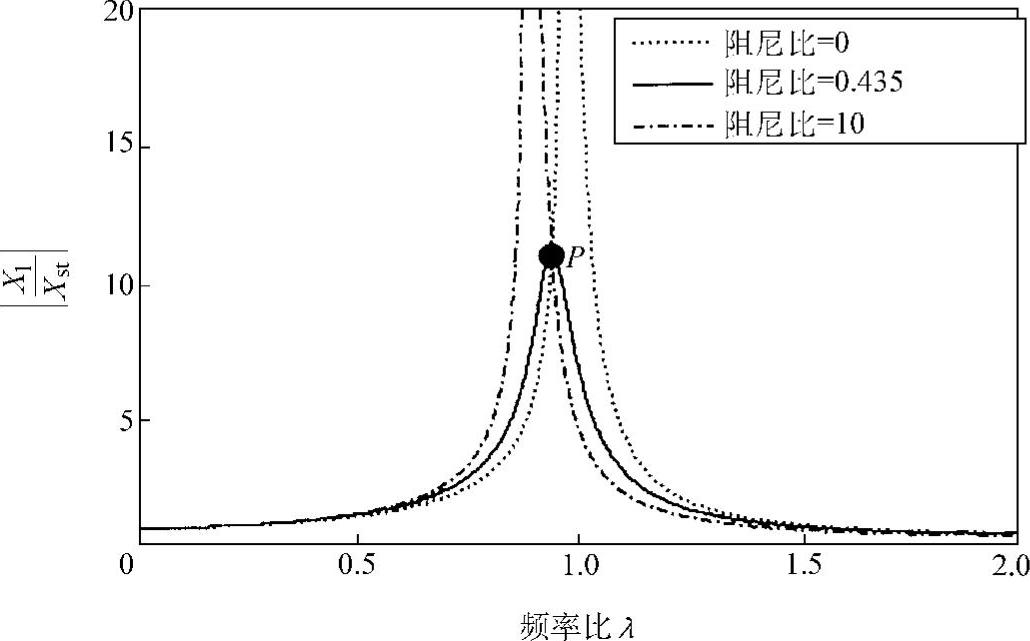
图2.25 Houde阻尼器的定点现象（μ=0.2）(www.xing528.com)

4.Frahm吸振器

如果去掉图2.13中的阻尼元件，则成为如图2.27所示的Frahm吸振器。事实上，这是世界上最早的动力吸振器，是由Frahm在1909年发明的。

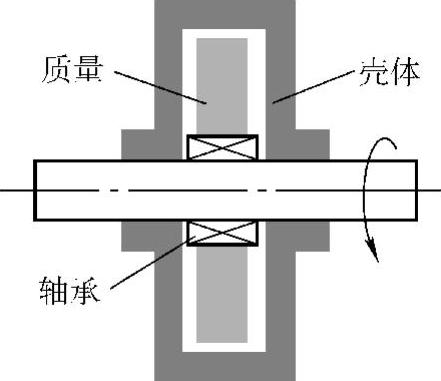
图2.26 用于控制轴的扭转振动的Houde阻尼器

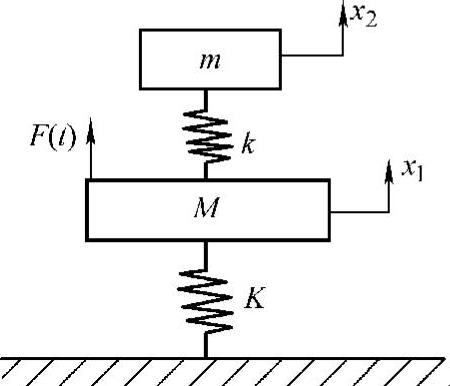
图2.27 Frahm吸振器的模型

对于如图2.27所示的振动模型，容易得到主振动系的振幅和附加质量的振幅为

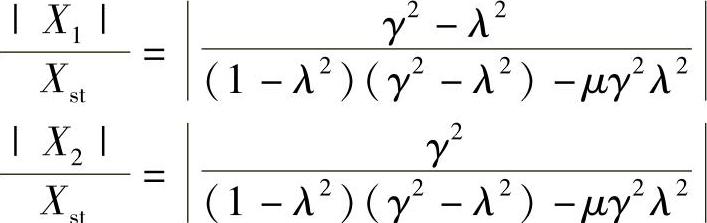
容易发现，当γ=λ时，即动力吸振器的固有频率与激振频率相等时，主振动系的振幅为0，动力吸振器的振幅倍率为1/（μγ²）。Frahm吸振器就是利用了这个现象。在已知主振动系的激励频率且其固定不变的情况下，可以调节动力吸振器的固有频率，使之与激励频率相吻合，这时，主振动系的振动会被完全消除掉，动力吸振器通过弹簧施加在主振动系上的力（等于动力吸振器的惯性力）与激励力大小相等，方向相反，所以主振动系停止不动。由于应用动力吸振器的主要目的是抑制主振动系的共振，所以Frahm吸振器的固有频率一般就选为主振动系的固有频率，即γ=1。

此外，上面两个关系式的右边具有同样的分母。由于分母为0时振幅为无穷大，对应于共振状态，可以得到附加吸振器后的系统的发生共振的条件为（γ=1的情况下）

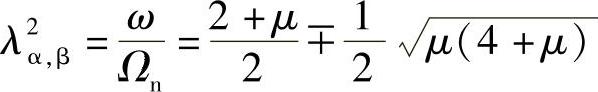
即当激励频率为ω=λ_αΩ_n或ω=λ_βΩ_n时，主振动系和动力吸振器的振幅变为无限大（见图2.28）。也就是说，原有系统的一个共振频率在附加上动力吸振器后，变成了两个共振频率。所以，Frahm动力吸振器不会改善系统的瞬态响应，而只能瞄准频率稳定不变的单频振动。正因如此，Frahm吸振器只能应用于某些特殊的情况下。

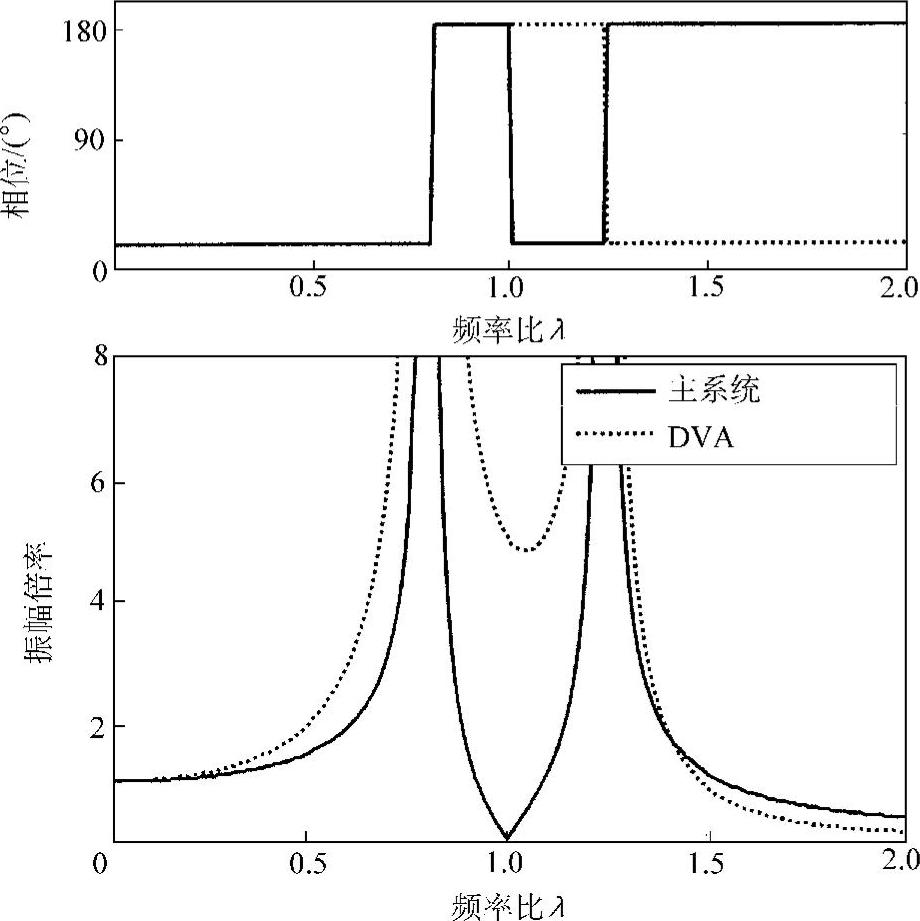
图2.28 Frahm动力吸振器的响应（γ=1）

5.冲击吸振器

作为利用附加质量控制主振动系振动的又一种方式，图2.29所示为冲击吸振器的模型。图2.29a是只有一个冲击块的模型；图2.29b是更为常用的粒子冲击吸振器，俗称“豆包阻尼”。冲击吸振器是利用动量转移及摩擦来实现控制振动的目的。一般是通过实验的方法来优化冲击吸振器的设计。

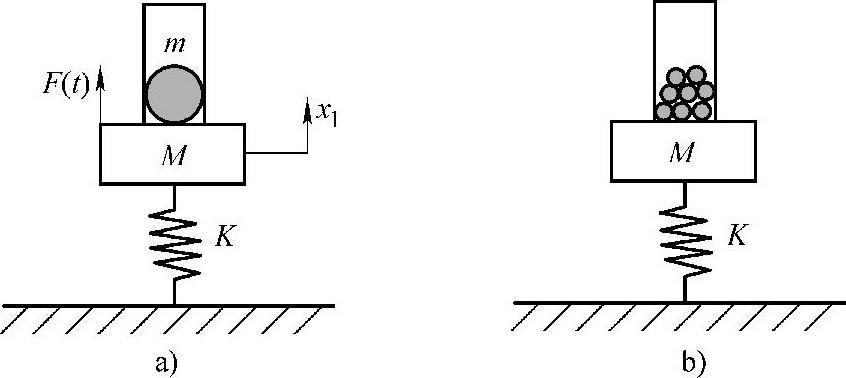
图2.29 冲击吸振器的模型

a）只有一个冲击块的模型 b）常用的粒子冲击吸振器

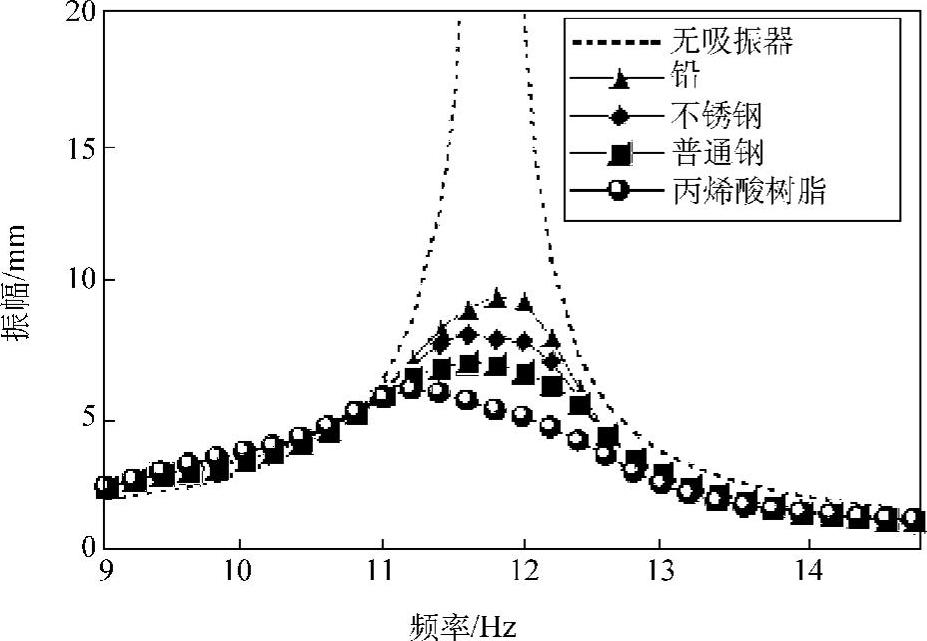
图2.30 微粒冲击吸振器的阻尼效果（质量比=0.138）

近年，利用离散元方法（Discrete Element Method，DEM）对粒子冲击吸振器进行数值分析取得了很大进展。例如某研究利用DEM和实验方法对粒子冲击吸振器的减振效果进行了对比，取得了很好的一致。该研究在粒子总质量与主振动系的质量之比保持相同的情况下，用4种不同材料（铅、不锈钢、普通钢、丙烯酸树脂）做成的“豆包”阻尼（单个球体直径为6mm）进行了控制一个单自由度系统振动的实验和解析。结果显示，粒子冲击吸振器具有良好的阻尼效果，而且在质量比相同的情况下，粒子的个体越多，阻尼效果越好（见图2.30）。

6.空气脉动阻尼（Air Squeeze Film Damper）

以上介绍的各种吸振器都借助于附加质量，通过附加质量的惯性作用提供控制主振动系的反作用力。这里介绍一种不需要附加质量，而是利用空气的反抗力来控制振动的方法。

图2.31所示是一个两端固支薄板结构。其背面与刚体的基础结构之间有一个间隙，形成了一个空气层。在外力激励下，板发生振动。当板上、下振动时，空气层发生排气与吸气流动。由于空气的粘性及压缩性会产生抵抗薄板振动的阻尼力和弹性力，从而起到制振的作用。

利用商用流体解析软件STAR-CD和构造解析软件Abaqus对这个问题进行流体-结构耦合解析。用大小为0.5N的简谐激励力（1kHz）对板进行加振，在不同的间隙（空气层厚度）下考察板的振动。图2.32是间隙为1mm时的结果。其中，细线为不考虑空气影响的结果，粗线是考虑上空气影响的结果。可见，二者基本相同。当把间隙减小为0.02mm时，结果如图2.33所示。此时，相对于没有空气层影响的结果（细线），考虑上空气影响的结果（粗线）的振幅大大减小。也就是说，当间隙较大时，空气的影响可以忽略不计；当间隙较小时，空气的反抗力限制了结构的振动。这种方法可以有效地运用于精密机械的微振动控制中。

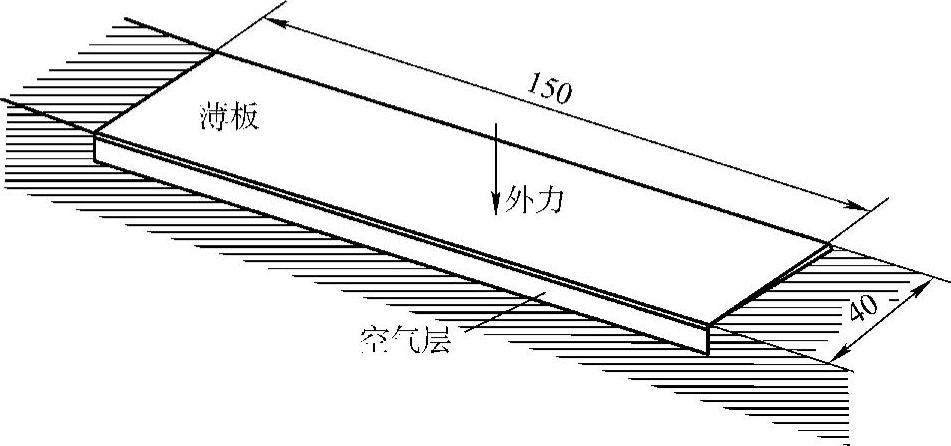
图2.31 背后有空气层的两端固支薄板结构

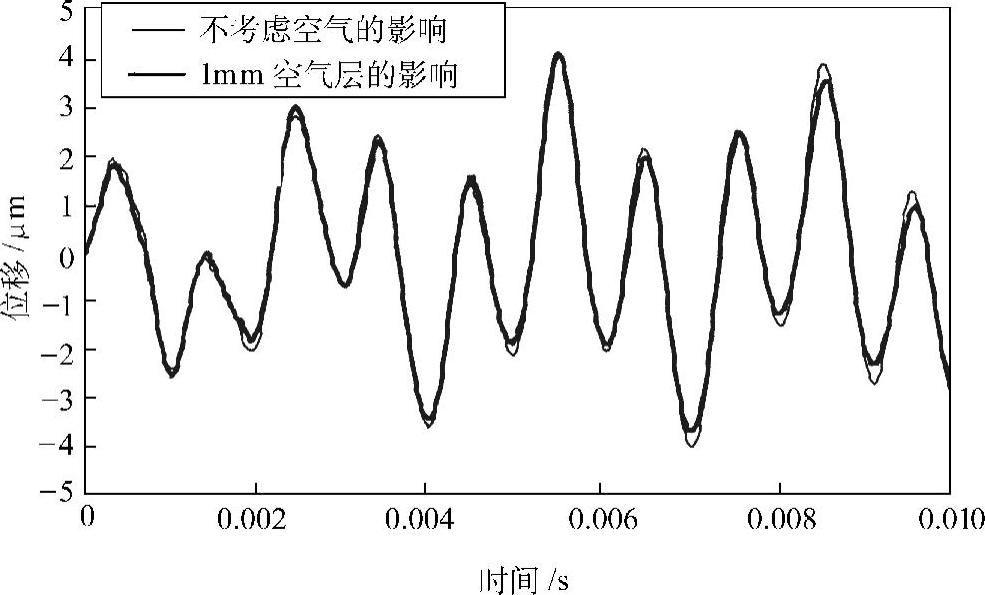
图2.32 间隙为1mm时的振动响应

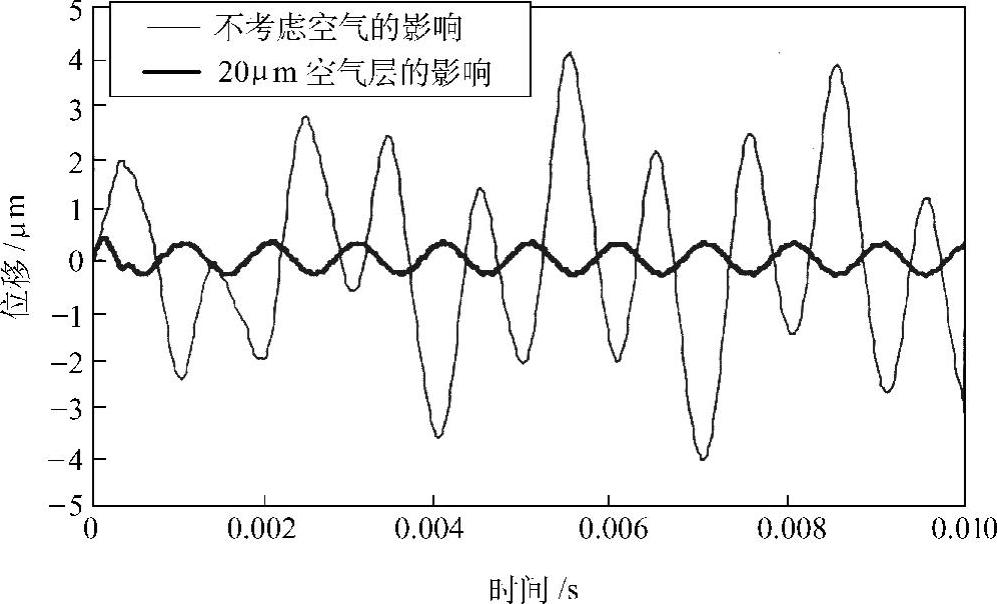
图2.33 间隙为20μm时的振动响应

图2.34为在间隙1mm和20μm两种情况下，薄板背后中央位置的空气压力与激励力相位关系的比较。间隙1mm时的空气压力很小，为了便于比较，把它扩大10倍表示在图中。可见，空气压力与激励力基本反相。进一步研究表明，当间隙很小时，空气的作用具有刚性和阻尼两重性质；而当间隙稍大时，空气基本上表现为阻尼作用。此处不做详细介绍。

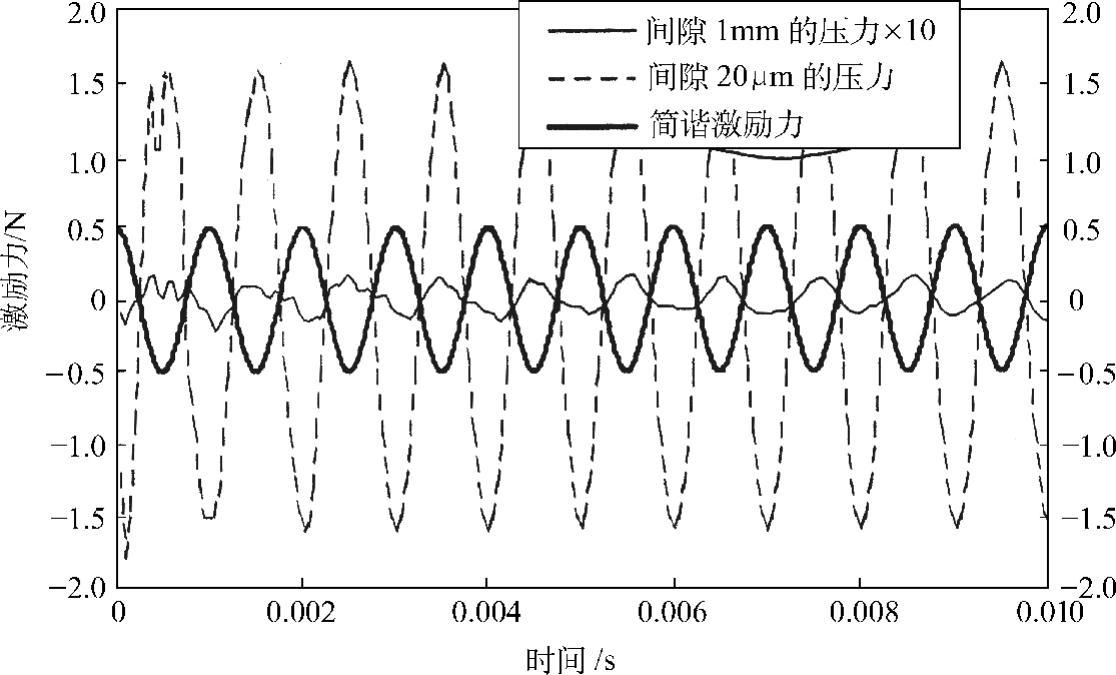
图2.34 不同间隙下的空气压力与激励力比较