动力吸振器设计中弹性元件应力和强度问题的考虑

以上，我们推导了动力吸振器的最优设计准则。我们的着眼点只是主振动系的振幅。这里，我们来比较一下动力吸振器本身的响应和主振动系的响应，以便对动力吸振器的工作原理有一个更深的理解。

求解方程式（2.20），可以得到动力吸振器本身的位移响应为

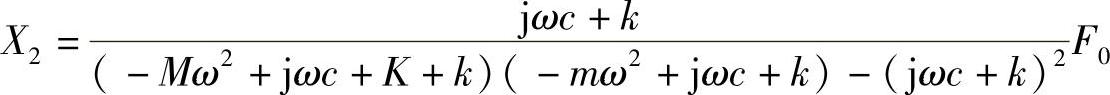
其振幅比率为

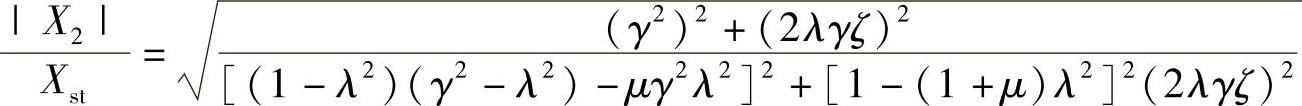
据此，我们可以绘制出动力吸振器本身的响应曲线，并与主振动系的响应做一下比较。

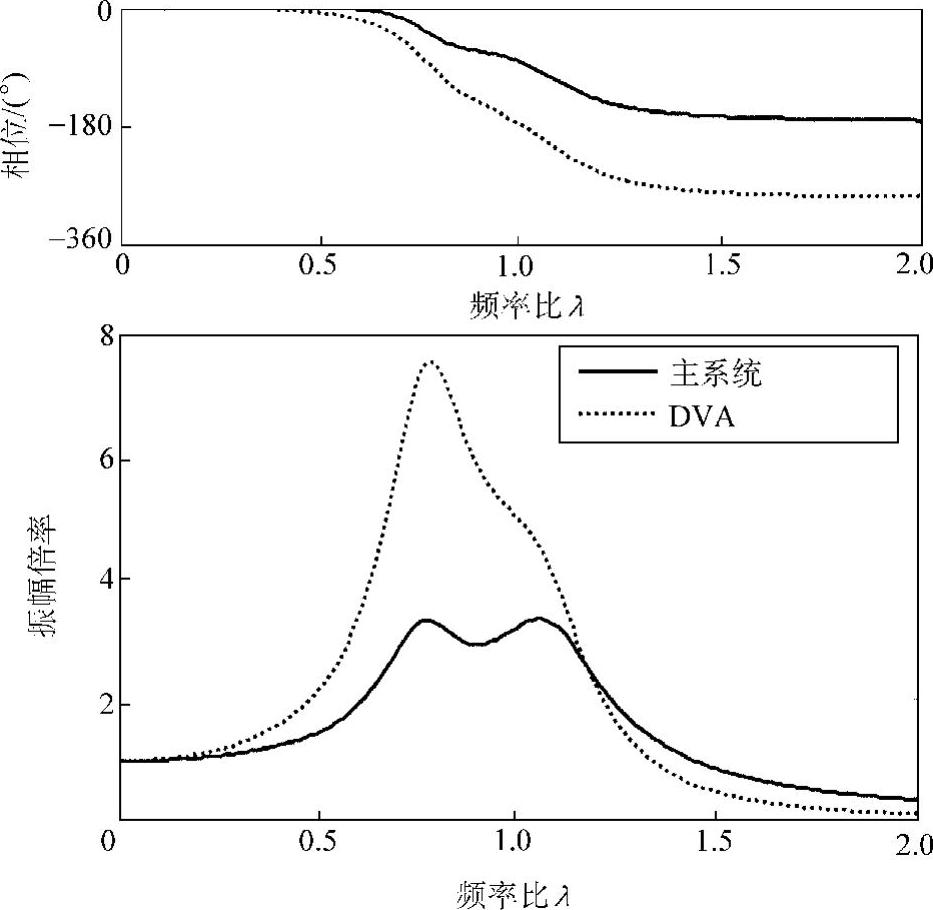
图2.16 最优状态下的响应（μ=0.2，γ_opt=0.833，ζ_opt=0.25）

图2.16是质量比为0.2的情况下，动力吸振器工作在最佳状态（最优同调γ_opt=0.833，最优阻尼ζ_opt=0.25）下的主振动系的频率响应和动力吸振器本身的频率响应的对比。动力吸振器本身的最大振幅比主振动系的振幅要大，并且相位与主振动系并不成180°反相关系，而是随激振频率发生变化。

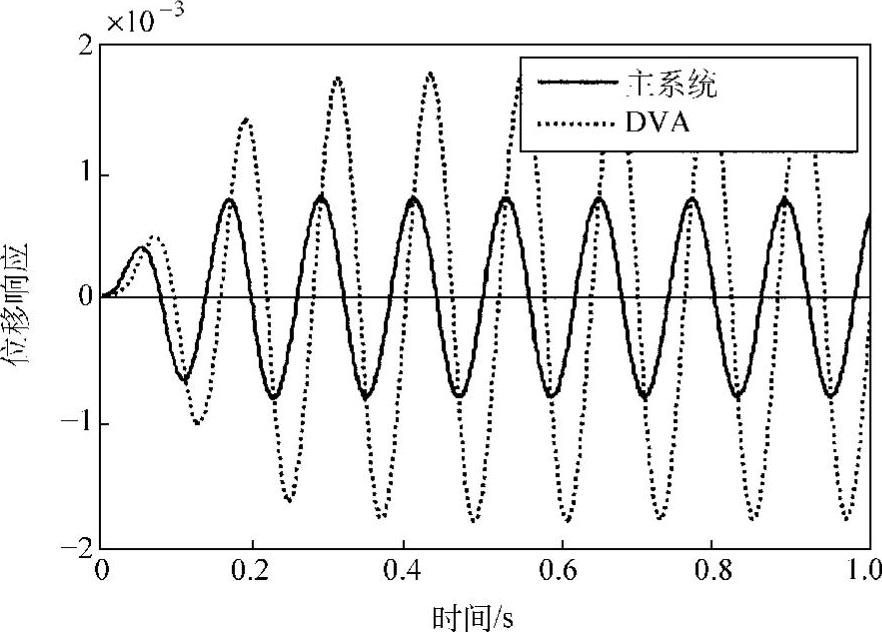
另外，我们也可以从时域响应来对二者进行对比。图2.17为在最优同调频率上用正弦外力激励主振动系时的强迫振动时间响应。图2.18为用单位脉冲激励的时间响应曲线。主振动系的振幅被减小的反面，动力吸振器本身却做较大的振动，相当于原有系统的一部分能量转移到了子系统上去。因此，在实际的动力吸振器设计中，应考虑到弹性元件的应力和强度问题。

(www.xing528.com)

图2.17 正弦激励下的响应（激励频率=最优同调频率，μ=0.2）

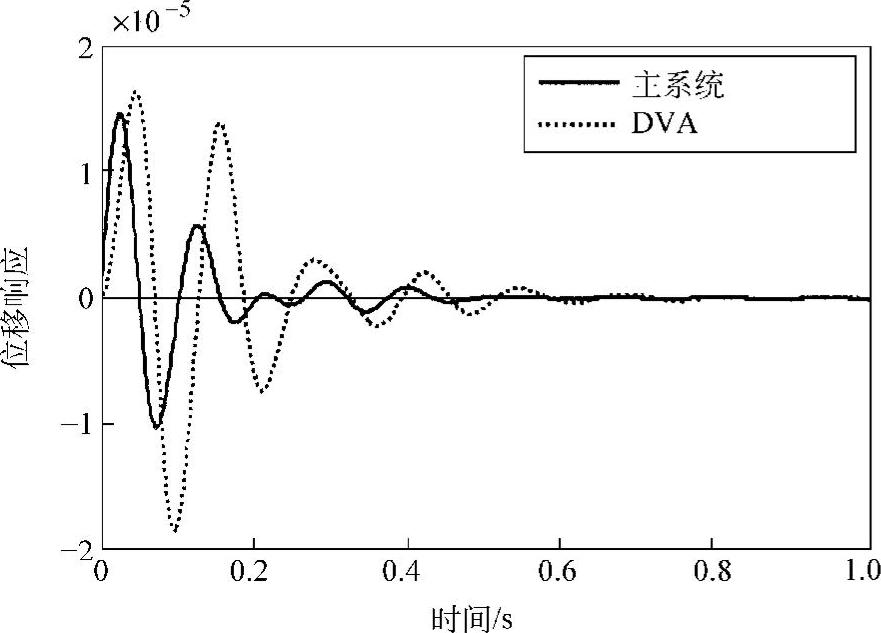
图2.18 脉冲激励下的响应（μ=0.2）

如果动力吸振器不是工作在最优状态会出现什么结果呢。作为一个例子，图2.19给出稍微偏离最优同调状态下的频率响应曲线。具体地说，相对于最优同调γ_opt=0.833和最优阻尼ζ_opt=0.25，这里取γ=0.8，ζ=0.2。可见，即使稍微偏离最优状态，主振动系的最大振幅就会有所恶化。因此，动力吸振器适合于控制具有突出峰值的窄带振动；对于没有突出谱峰的宽带振动，如白噪声信号，则动力吸振器的效果不易发挥。

动力吸振器能否长期稳定地工作在最优状态在实际应用中具有重要意义。影响动力吸振器性能的因素有：阻尼性能的经时变化、主振动系本身动特性的变化、外部动载荷的变化。选用不易受温度湿度影响的阻尼，如磁性阻尼，采用多重动力吸振器、增加吸振器的质量或主动控制的方法，是解决上述问题的有效对策。但是一般来说，实际系统的特性和工况变化不会太大，因此运用动力吸振器控制窄带振动总是可以获得或多或少的制振效果。

动力吸振器的质量越大，其控制效果越好。然而，在对产品的节能和低成本要求越来越高的今天，增加附加质量可以说是万不得已的选择。例如对于车体超过1000kg的汽车设计人员来说，采用一个1kg重的吸振器都是有抵抗感的事情。也就是说，最好的方法是对结构本身进行优化设计，以达到对振冲噪性能的要求。

最后需要指出的是，以上讨论的是单自由度系统的振动控制。在这种简单的情况下，最优同调公式（2.26）中的质量比（μ=m/M）就是吸振器的质量与主振动系的实际质量之比。对于弹性连续体结构的振动控制，M并不是结构的整体质量，而是指吸振器安装位置的等效质量。等效质量的确定方法将在下一章中进行介绍。

另外，如果考虑主振动系统的阻尼，则定点理论不再成立。这时可以运用数值方法进行优化设计。实际上，需要振动控制的地方往往阻尼很小，因此，上述针对无阻尼系统的动力吸振器的设计方法具有充分的实际应用价值。

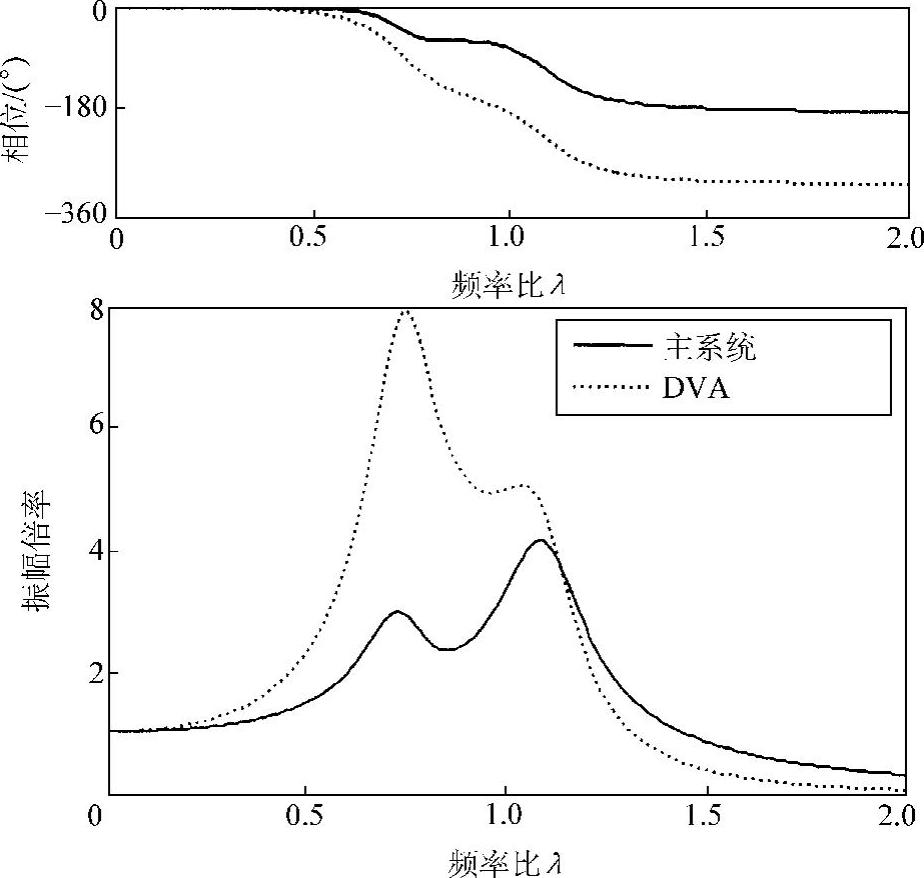
图2.19 非最优同调状态下的响应（μ=0.2，γ=0.8，ζ=0.2）