动力吸振器的定点理论设计

1928年，Ormondroyd和Den Hartog提出了利用动力吸振器的阻尼作用降低主振动系振幅的动力吸振器的设计思想，并指出了最优阻尼的存在。在此基础之上，Hahnkamm利用振幅曲线上存在两个不受阻尼大小影响的定点现象，推导出了动力吸振器的最优同调频率，Brock随后推导出了最优阻尼的关系。这就是现在广为人知的动力吸振器设计的定点理论。为了便于参考，本节对这个理论做详细介绍。

图2.13所示的二自由度系统的振动由以下运动方程决定

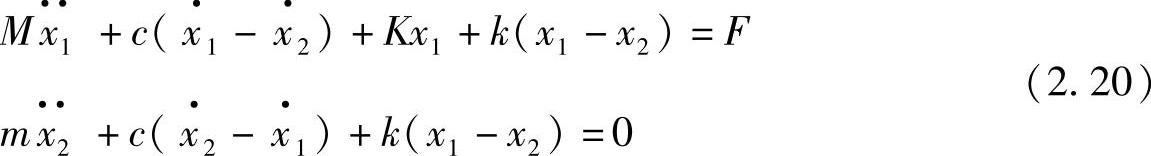
考虑简谐激励力的情况，F（t）=F₀e^jωt，则响应可以表示为

代入式（2.20），可以推导出

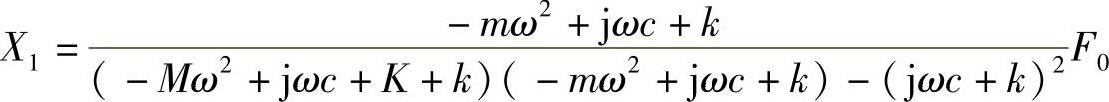
进一步应用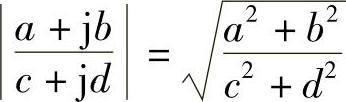的关系，可以推出主振动系的振幅为

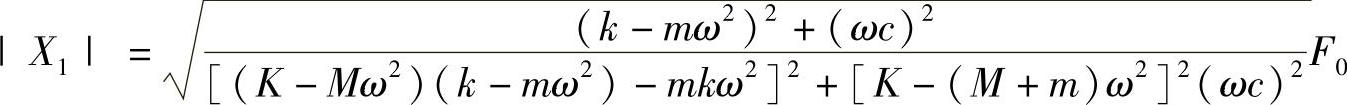
上式中各项同除以（Mm）2，并引入以下各项

质量比：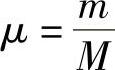

阻尼比：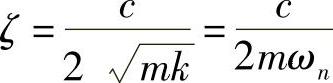

静变形：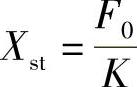

强迫振动频率比：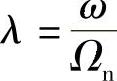

固有频率比：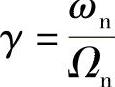

整理可得

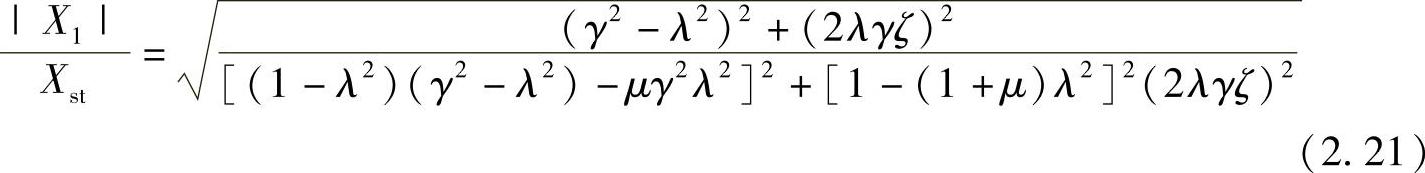
式（2.21）即是动力吸振器作用下的主振动系的振幅倍率。在给定质量比μ和固有频率比γ的情况下，可以计算出振幅。例如图2.14是在μ=0.2、γ=0.8的情况下，根据上式（2.21）绘制出来的几种不同阻尼比的振幅倍率曲线。当阻尼无限大时，相当于动力吸振器被固定在主振动系上，从而变成一个无阻尼单自由度系统的振动，共振振幅为无限大；当阻尼为0时，动力吸振器的作用是把原系统的共振频率分解为两个新的共振频率，振幅仍为无限大。所以，在0～∞之间，肯定存在一个最优阻尼值。图2.14有一个显而易见的特点，即所有不同阻尼比的曲线有两个共同的交点P、Q。也就是说，P、Q点的位置不受阻尼的影响，这就是所谓的定点现象。下面，我们来介绍如何利用这个定点现象来进行动力吸振器的最优设计。

观察图2.14，要使主振动系的振幅最小，设法使P、Q点等高，并且使它们成为曲线上的最高点即可达到目的。P、Q点的位置不受阻尼的影响，却受固有频率比γ的影响。动力吸振器优化设计的第一个任务就是寻找最佳固有频率比γ，以使P、Q点等高。这个状态称为最优同调状态。因此，动力吸振器也被称为Tuned Mass Damper（TMD）。优化设计的下一步则是寻找最佳阻尼，使得P、Q点处于曲线的最高点。

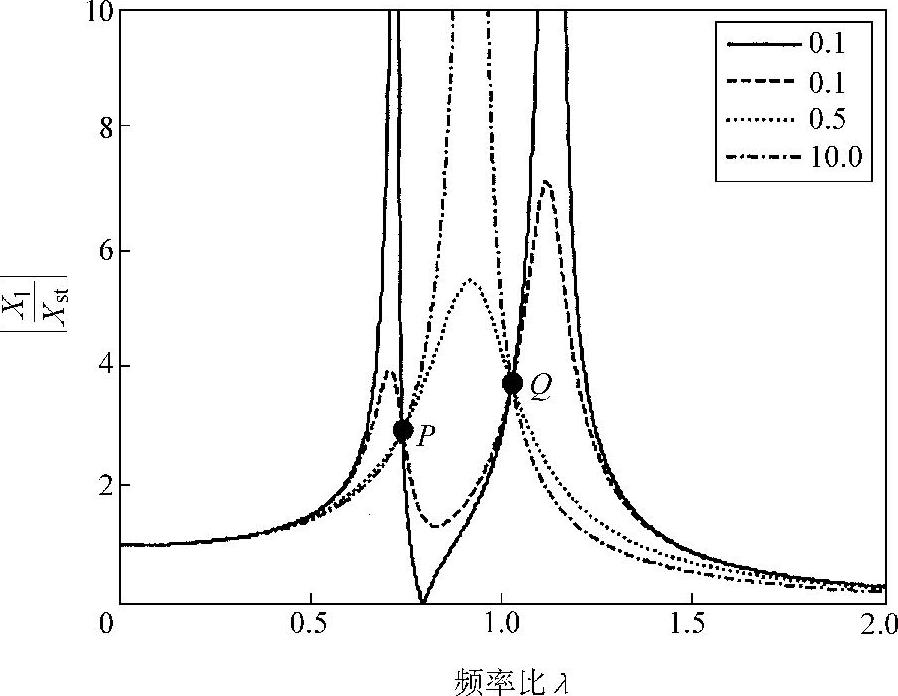
图2.14 几种不同阻尼比情况下的振幅倍率曲线（μ=0.2，γ=0.8）

1.最优同调频率的决定

将式（2.21）根号下分子用p代表，分母用q代表，并做以下变形

p=A+Bζ²，q=C+Dζ²

其中，A=（γ²-λ²）²，B=（2λγ）²，

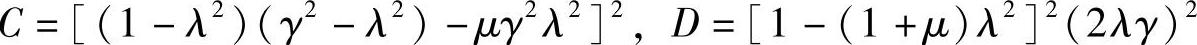
则有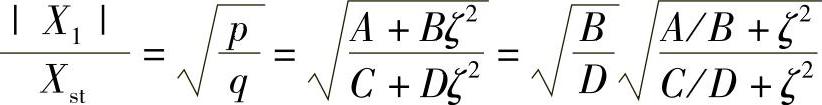容易发现，在A/B=C/D，即A/C=B/D的条件下

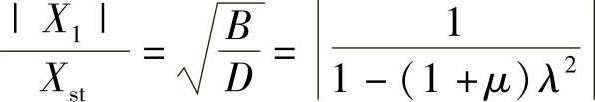
所以，振幅响应与阻尼无关。此外，ζ=0和ζ=∞两个特殊情况下的振幅分别为

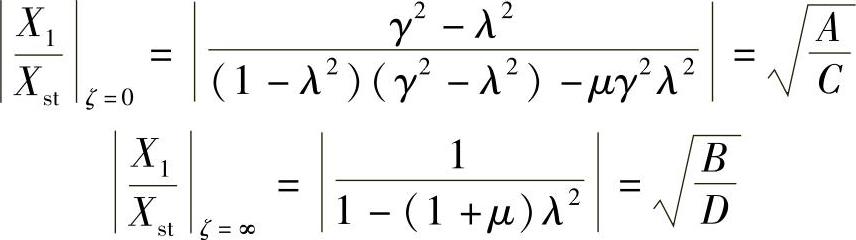
A/C=B/D的条件意味着ζ=0和ζ=∞的振幅曲线的交点，即P、Q点。由于P、Q点分别处于振幅曲线的相反边上（容易证明，ζ=0和ζ=∞的响应正好反相），定点的位置由以下关系式所决定

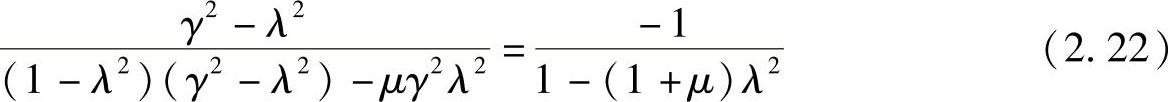
整理可得

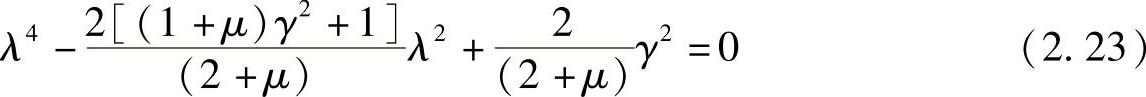
设式（2.23）有两个根λ_P、λ_Q，则有下列关系

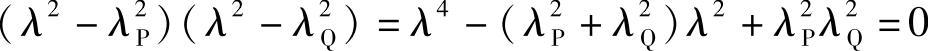
与式（2.23）对比，可得

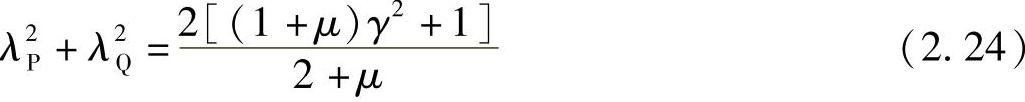(www.xing528.com)

此外，为了达到最优同调，P、Q点的响应应该相等，因此有

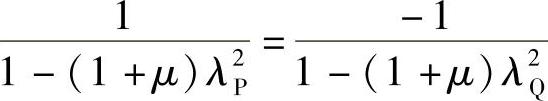
整理得

由式（2.24）和式（2.25），可以求得最优同调频率比为

也就是说，当动力吸振器的固有频率为主振动系固有频率的1/（1+μ）倍时，两个定点P、Q的振幅相等。图2.15是在最优同调状态下的不同阻尼比的振幅倍率曲线（μ=0.2，γ_opt=0.833），与图2.14相比，P、Q点变为等高（图中细实线为后述的最优阻尼的情况）。

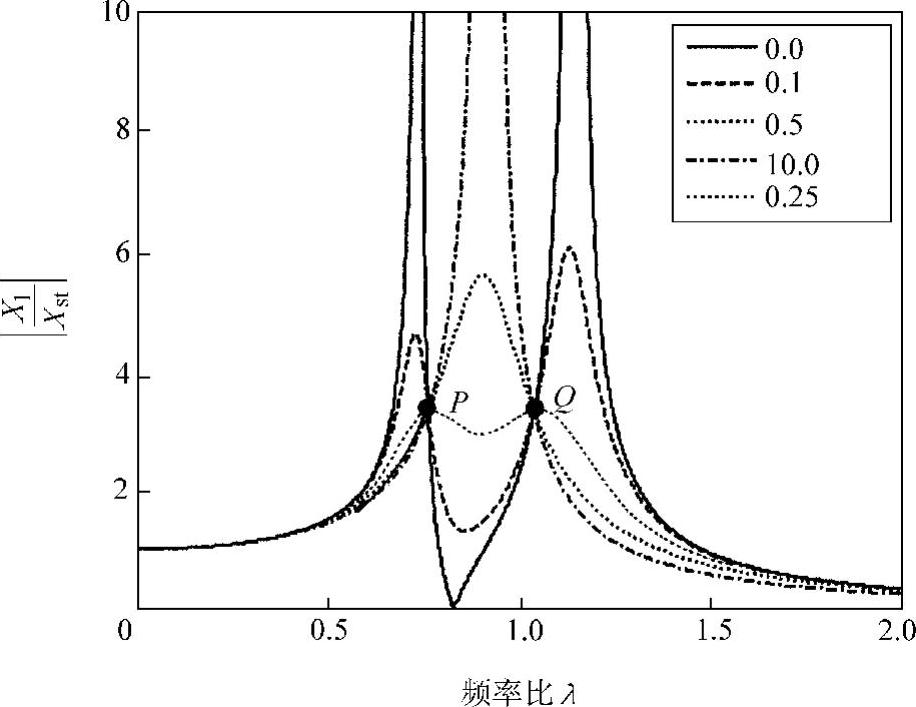
图2.15 最优同调状态下的不同阻尼比的振幅倍率曲线（μ=0.2，γ_opt=0.833）

将式（2.26）代入式（2.23），可以求得P、Q点在频率轴上的位置为

将式（2.26）和式（2.27）代入式（2.21），可以得到定点的振幅为

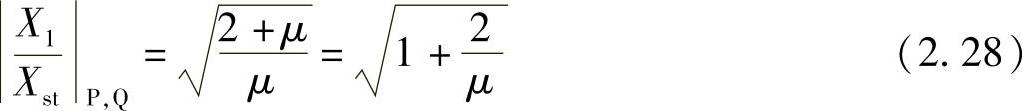
例如μ=0.1时，定点的振幅倍率为4.58；μ=0.2时，定点的振幅倍率为3.32。动力吸振器的质量越大，振动控制效果越好。

2.最优阻尼的决定

仅仅是让P、Q点等高并不是我们的最终目的，只有当P、Q点处于振幅曲线上的最高点时，振幅最大值才最小。这个条件由阻尼的大小决定。这里，我们来看最优阻尼的决定方法。

P、Q点处于振幅曲线上的最高点，意味着经过这两个点的曲线斜率为0，即

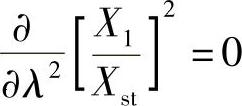
或者写成以下形式

p′q-pq′=0 （2.29）

这里，p′=∂p/λ²，q′=∂q/λ²。

在最优同调条件下，有

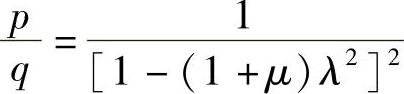
代入式（2.29），可得

由p、q的定义

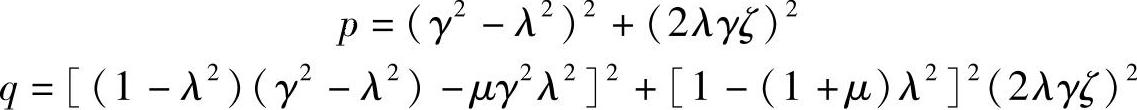
可得对于λ²的微分为

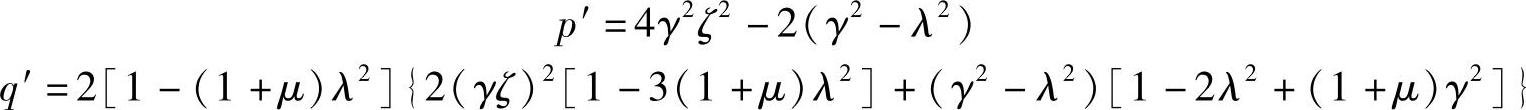
在求q′时，用到了最优同调的关系式（2.22）。代入式（2.30）并求解ζ²，可得

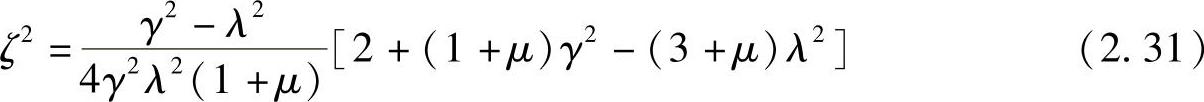
进一步将式（2.26）和式（2.27）代入整理，可得

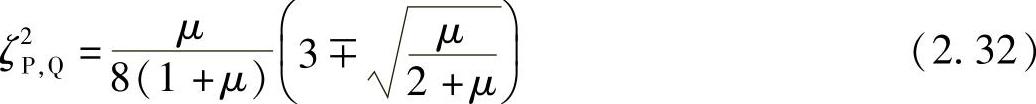
可见，使P点为极大和使Q点为极大的阻尼值并不相同，因此严格地讲，并不存在一个最优阻尼值，使得P、Q点同时为最大。但是，无论是取哪一个值，所得结果的差异都很小，因此合理的做法就是取ζ²_P、ζ²_Q的平均，从而得到最优阻尼为

图2.15中的细实线为最优阻尼时（ζ_opt=0.25）的振幅曲线。显然，P、Q点处于这个曲线上的最高点。这是在给定质量比的情况下，动力吸振器所能达到的最好效果。