在前面的讨论中,基础结构要么被认为固定不动,要么被认为做强制运动。这意味着基础结构被当作刚体看待。这种近似在很多实际情况中是合理的,例如对于安装在地板上的机器设备来说,与基础结构(大地)相比,其质量很小,基础结构可以看作为具有无限大质量的刚体。但是,在有些情况下,这种假设就不成立。例如300kg的汽车发动机安装在1000kg的车体上,把车体当作刚体看待就有些勉强;对于安装在船体上的大型柴油发动机和安装在机翅下的飞机发动机来说,发动机的质量远大于安装部位本体结构的质量,这时把支持结构当作刚体明显不合理。
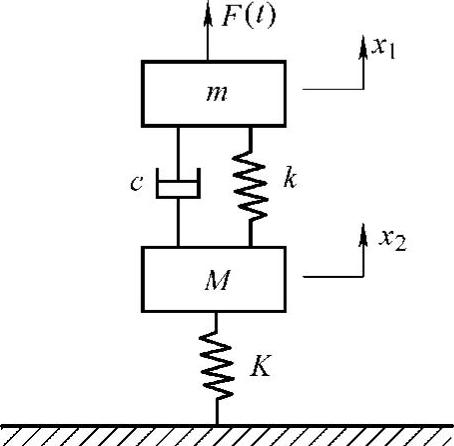
图2.5 二自由度系统振动模型
本节来讨论考虑到支持结构动特性的隔振问题。这是一个很复杂的问题,为了简单,我们把支持结构简化为一个由质量M和弹簧K组成的系统。这样,整个振动系统可以用一个二自由度系统来建模,如图2.5所示。
在前面各章节中,我们仅限于对单自由度系统的讨论。在此,首次引入二自由度振动系统。对于二自由度或多自由度来说,可以对每个质点列出其动力平衡方程,然后联立起来,即可得到整个系统的运动方程。对于如图2.5所示的系统,其运动方程为
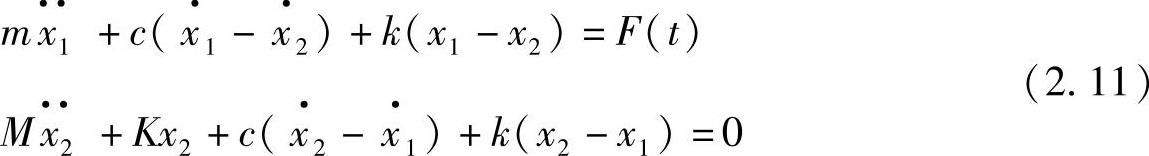
对于设备隔振的情况,我们所关心的是基础结构的振动以及传递到其上的力。为了求解方便,运用1.2节所介绍的复指数的表达方法,设激励力F(t)=F0ejωt,位移响应分别为x1=x1mejωt、x2=x2mejωt,这里,x1m、x2m可能是复数。代入式(2.11)整理
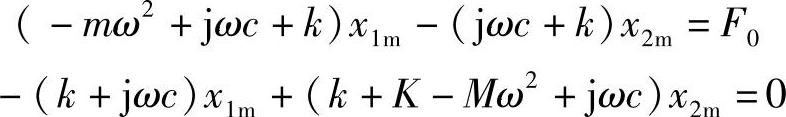
求解,可得
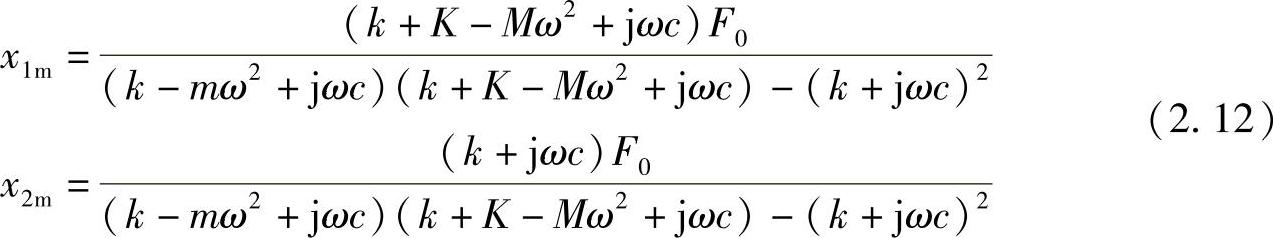
传递到基础结构M上去的力的大小为
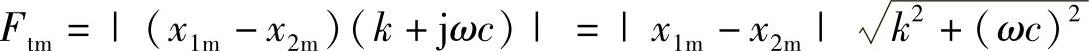
将式(2.12)代入并整理,可得
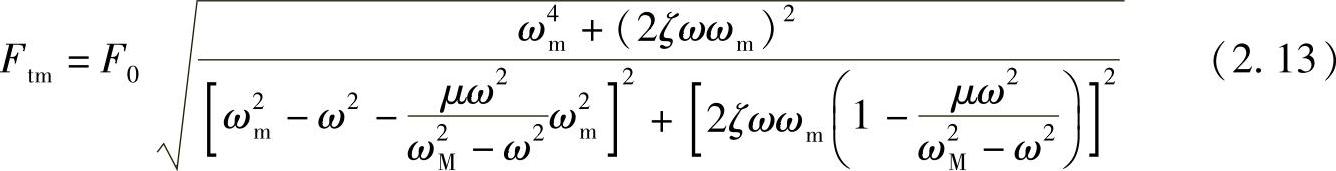
其中,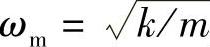 为设备系统单独的固有频率,
为设备系统单独的固有频率,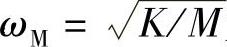 为基础结构单独的固有频率,
为基础结构单独的固有频率,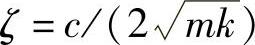 为阻尼比,μ=m/M为质量比。进一步引入无量纲参数β=ω/ωm,γ=ωm/ωM,可得力的传递率为
为阻尼比,μ=m/M为质量比。进一步引入无量纲参数β=ω/ωm,γ=ωm/ωM,可得力的传递率为
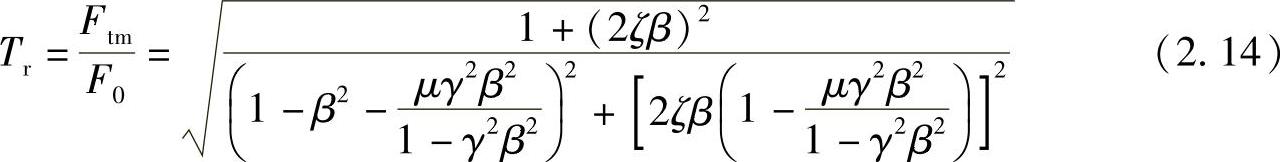 (https://www.xing528.com)
(https://www.xing528.com)
式(2.14)与式(2.4)形式相似,只是分母中多了一个μγ2β2/(1-γ2β2)的项。当γ2β2=1,即ω=ωM时,式(2.14)的分母为无限大,力传递率为0,在其曲线上产生一个下凹(notch)。在γ2β2>>1,即ω>>ωM的领域,μγ2β2/(1-γ2β2)≈-μ,式(2.14)可以近似为
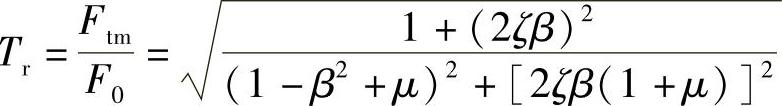
对于基础结构的质量非常大的情况,μ<<1,上式与式(2.4)等价,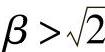 为隔振领域。
为隔振领域。
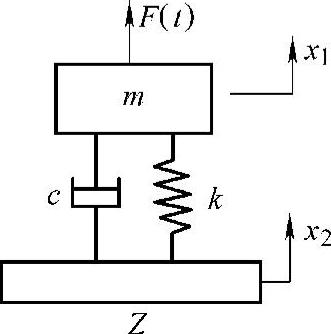
图2.6 用阻抗代表基础结构的振动模型
以上把基础结构用一个质量弹簧系统来代表,显然大大简化了实际结构的复杂性。但即使是这种简单的模型,参数M、K也并不容易给出。为了考虑更为一般的情况,引入阻抗的概念。一个动态激励力F作用在结构上,在作用点产生的位移响应为x,则该点的机械阻抗(Impedance)定义为
Z=F/x (2.15)
Z一般为复数。对于参数未知的基础结构,可以测量到设备安装位置的阻抗,建立如图2.6所示的模型。于是,可以得到下列方程
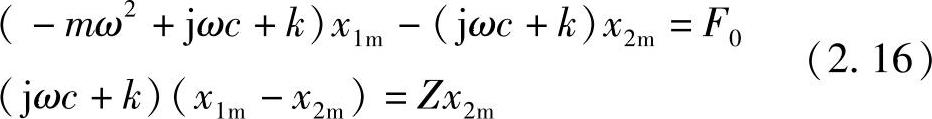
求解这个联立方程,可得
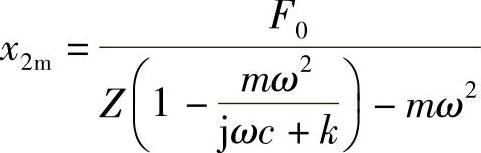
由于传递到基础结构上去的力的幅值为
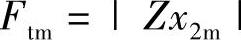
将x2m的表达式代入,可得力的传递率为
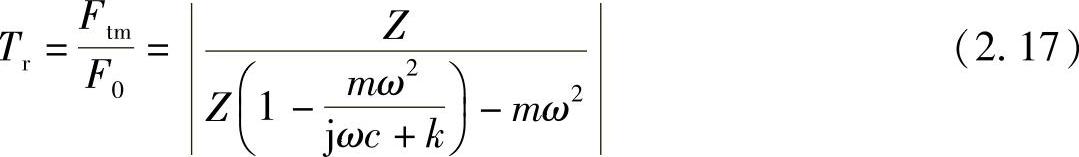
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




