设备隔振：减少振动传递到基础结构的隔离机器优化方案

首先来讨论避免机器的振动向周围传播的情况。这种情况的最简单模型仍然可以沿用上一章中所讨论的单自由度振动系统，如图2.2所示。在这里，振动的机器被简化成一个刚体质量，它与固定不动的基础结构之间的结合被简化为一个弹簧和阻尼元件。当弹簧刚性无限大时，即相当于物体被固定在基础结构上的情况。

图2.2 隔振的单自由度振动模型

考虑机器在正弦激励力F（t）=F₀ sinωt作用下的强迫振动。这个激励力可以来自外界，也可能产生于机器内部，如旋转部件的偏心所引起的作用力。而机器对基础结构（如地面）的作用力为从弹簧元件传来的作用力和从阻尼元件传来的作用力之和，F_t=F_k+F_c。

由1.3.3节的结果可知，机器的稳态振动响应为

x=Xsin（ωt-ψ） （2.1）

其中，幅频特性和相频特性分别为

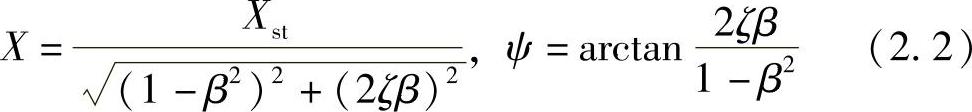
这里，，，，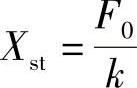

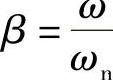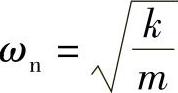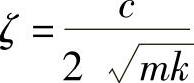
于是，传到基础结构上的力为

其中，θ=arctan（cω/k）=arctan（2ζβ）。将式（2.2）代入上式并整理，可得

(www.xing528.com)

如果用F_tm表示上述传递力的幅值，则有以下关系

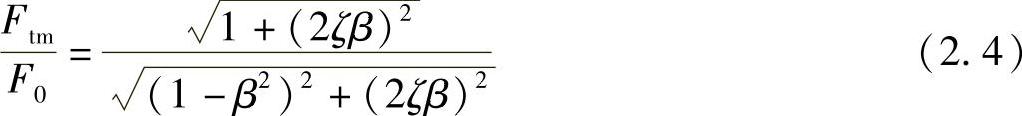
上式代表激励力传递到基础结构上去的比率，称为力的传递率。也容易得出，传递到基础结构上的力与激励力之间的相位差为

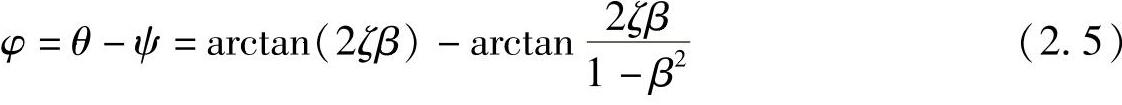
如图2.3所示为根据以上结果绘制的振动传递曲线。这里，我们讨论下列情况。

1）机器与基础结构之间刚性结合的情况。在这种情况下，相当于图2.2中的弹簧刚性为无穷大，因此有ω_n=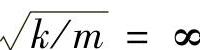，β=ω/ω_n=0，F_tm/F₀=1，即振动传递率的幅值为1。也就是说，作用在机器上的激励力100%地传递到了基础结构上。事实上，这时的振动传递问题已经变成一个单纯的静态力的传递问题，与人们的直感较易吻合，因此容易理解。

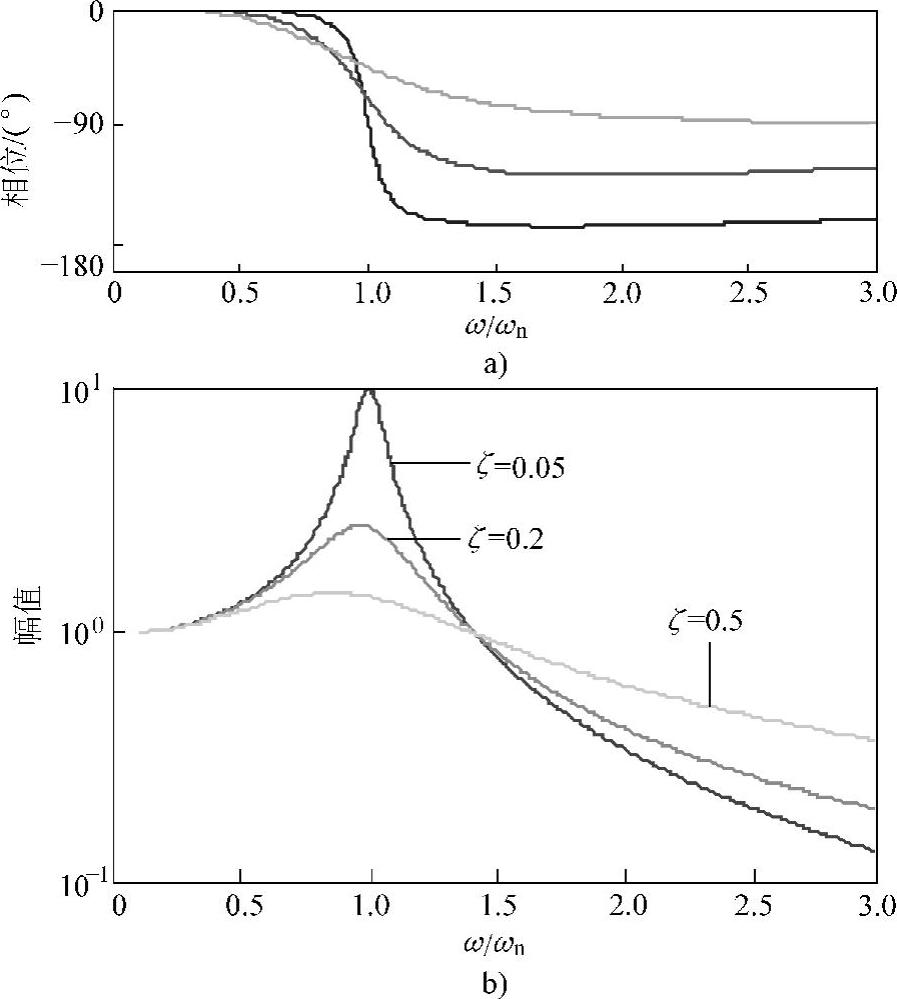
图2.3 单自由度振动系统的力的传递率

a）相频特性 b）幅频特性

2）机器发生共振的情况。如果弹性支撑的刚性恰好使得物体在激励力的作用下产生共振，则传递到基础结构上的力远远大于激励力本身的幅值。这时，非但起不到隔振的效果，反而使得问题恶化。这是隔振设计最应避免的情况。

3）激励力频率为固有频率的倍以上的情况。由式（2.4）可知，当β=ω/ω_n=2时，振动传递率的幅值为1；而对于的情况，则振动传递率的幅值小于1。这时，传递到基础结构上的力小于激励力，也就是说，隔振效果才得以体现。因此，所谓隔振设计，就是选择适当的柔性支撑把机器与基础结构相结合，构成一个低频振动系统，使得机器工作在远远大于该系统的固有频率的领域。

4）阻尼对隔振效果的影响。一方面，由图2.3可见，在共振区域，增加弹性支撑的阻尼，可以有效地抑制振动传递率的增加；另一方面，在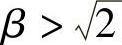的隔振领域，增加阻尼反而会降低隔振效果。因此，阻尼在隔振系统中的作用具有两重性，需要慎重考虑。一般来说，防止共振时的大幅恶化更为重要，适当的阻尼对于隔振系统来说必不可少。