机械振动自激振动的力学模型

自激振动有多种形式，由于摩擦引起的自激振动是最常见的一种形式。如图1.35所示为干摩擦引起的自激振动的力学模型。由质量和弹簧组成的单自由度系统相当于琴弦，与之接触的传输带相当于琴弓，二者之间存在摩擦作用。假定除了摩擦力之外，在运动方向上没有其他外力作用在质量m上。质量对传输带的正压力为N，摩擦因数为μ，传输带稳态转动速度为一恒定值V。

首先，我们来考查如图1.19所示的理想的库仑摩擦特性，即摩擦因数为一定值时，不存在静、动摩擦因数之别的情况。如果传输带在由静止状态到达稳定运转状态的起动过程是一个非常缓慢的准静态的过程，则作用在质量上的摩擦力也相当于一个静态力。即质量在摩擦力的作用下随着传输带一起向右运动，摩擦力在与弹簧恢复力保持平衡的状态下逐渐增大；当质量到达位置x=Nμ/k时，摩擦力达到最大；此后，质量与传输带脱离，发生相对运动。但是，由于没有静、动摩擦之别，虽然产生了相对运动，摩擦力的大小保持不变，因此质量仍然保持在x=Nμ/k位置的静止平衡状态，不发生振动。

如果传输带的起动过程比较短暂，是一个动态变化过程，则质量的加速度不可忽略。此时，与摩擦力保持平衡的不光是弹簧恢复力，还有惯性力。其运动方程为

这里，我们假定在时间t₀内，质量在传输带的带动下一起运动，此后二者分离；并假定摩擦力的变化如图1.36所示，则方程式（1.89）相当于在1.6节所讨论的任意形式激励力作用下的振动情况。

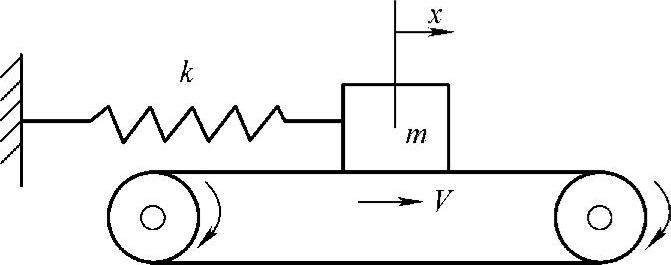
图1.35 干摩擦引起的自激振动的力学模型

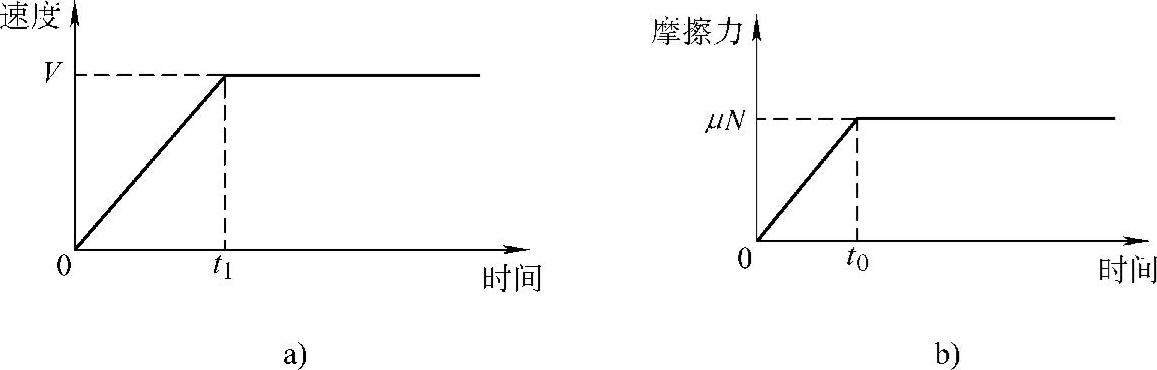
图1.36 传输带的起动过程与摩擦力的变化

a）传输带的起动过程 b）传输带摩擦力的变化

我们运用1.6.3节所介绍的拉普拉斯变换法来求解方程式（1.89）的解。考虑初始位移和初始速度均为0的条件，通过对方程式（1.89）两边进行拉普拉斯变换，可以求得

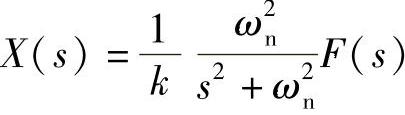
另外，根据拉普拉斯变换的定义，可以得到如图1.36所示摩擦力的拉氏变换为

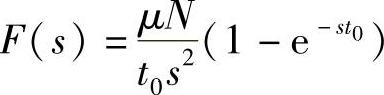
因此可得

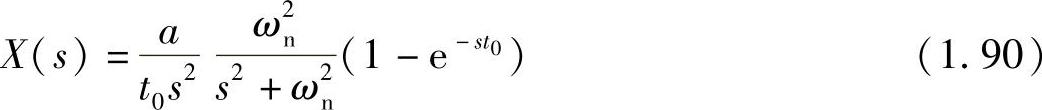
其中，a=μN/k。然后，利用以下拉氏逆变换公式

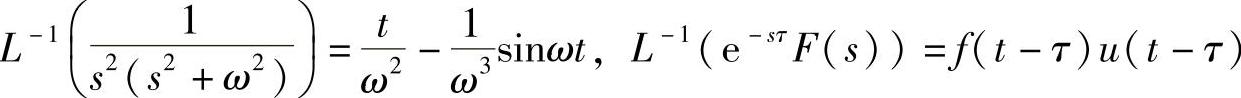
可以求得位移的时间响应为

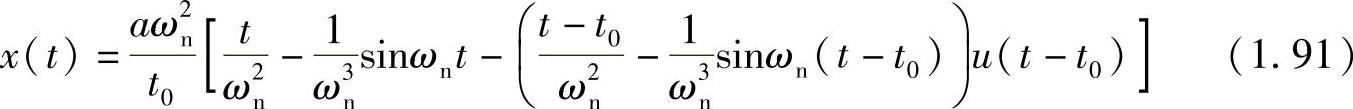
其中，u为单位阶跃函数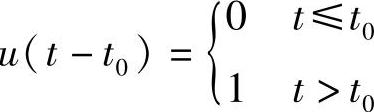，。考虑t＞t₀以后的响应，则有

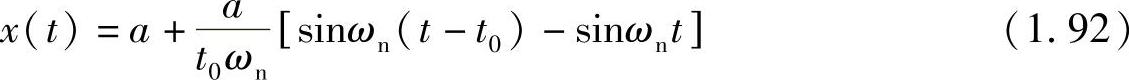
相应的速度为

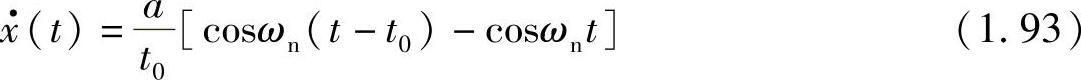
随着时间的推移，t>>t₀，t-t₀≈t，可以得到x（t）≈a、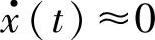的结果，即质量最终停止于静态平衡位置。当t₀=2πn/ω_n（n=1，2，…）时，可以得出x（t）=a、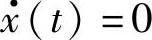，也就是说，当t₀等于系统的固有周期的整数倍时，质量一直处于静态平衡位置，不发生振动。

以上讨论的是质量事先放在传输带上，传输带由静止到转动的情况。这里，我们再来讨论另一种情况：质量事先与传输带不接触，传输带以恒定速度V运转；在某时刻，质量突然与传输带开始接触。在这种情况下，质量在传输带的带动下以速度V向右运动，在x=Nμ/k处二者脱离。因此，发生的摩擦力仍然可以用如图1.36b所示的特性来表示，式（1.92）和式（1.93）所代表的位移和速度响应依然成立，只不过此时的t₀具有一个确切的值：

t₀=a/V=μN/（kV）

代入式（1.92）和式（1.93），并进行三角函数变换可得

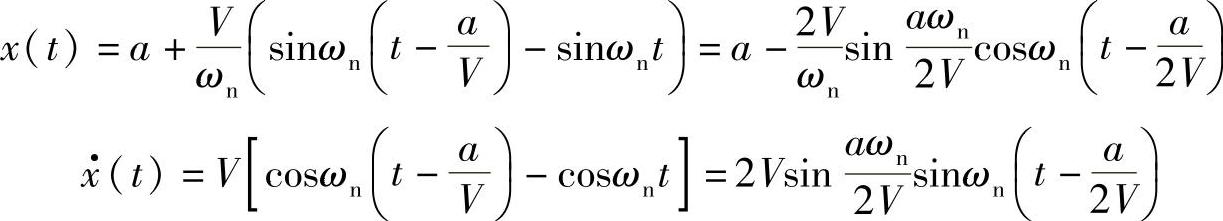
可见，这是一个以x=a为原点的简谐振动，振动频率即为系统的固有频率。如果V比较大，以至于aω_n/2V<<1，sin（aω_n/2V）≈aω_n/2V，则有

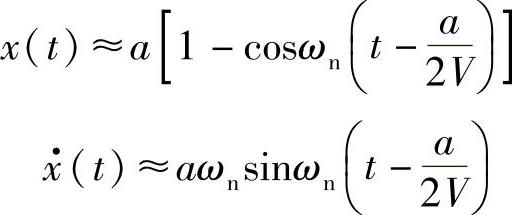
即位移的振幅不再随V变化，总是等于a，而速度的振幅为aω_n。

对于一个固有频率为100Hz的系统，图1.37a描绘出不同运转速度下的质量的位移曲线（单位：mm）。对于V=5mm/s和V=10mm/s两种情况，振幅已经保持不变，约等于a。通常，a非常小，上述振动是一个微振幅振动。由于在上面的讨论中没有考虑系统的阻尼，因此所得结果为不衰减振动。图1.37b给出考虑到阻尼（阻尼比为0.1）的响应（计算公式略），可见在阻尼作用下，这个微振幅振动会很快地衰减掉。

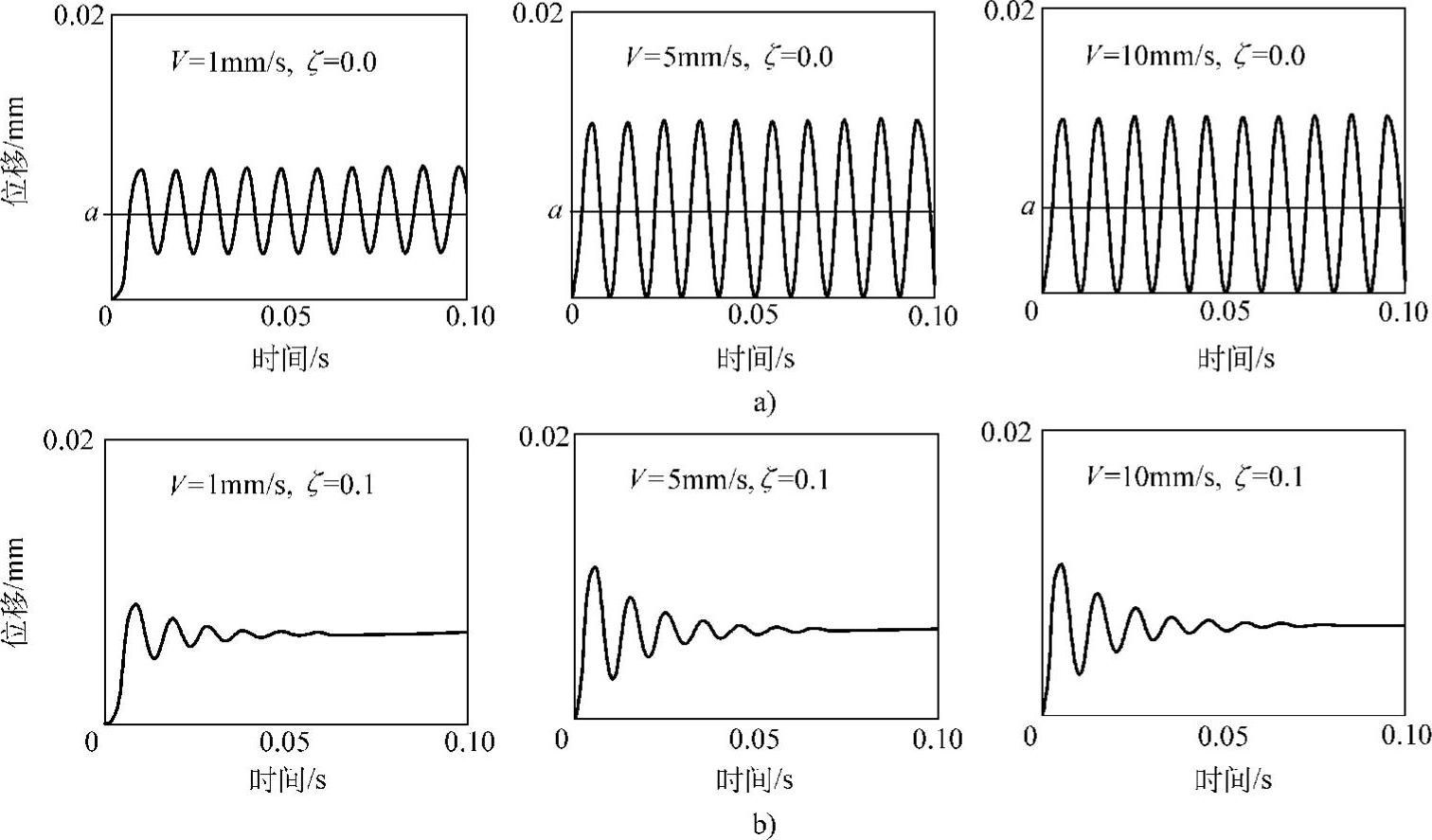
图1.37 不同运转速度下的位移（m=1kg，μ=0.25，f_n=100Hz）

a）无阻尼时的不同运转速度下的位移 b）有阻尼时的不同运转速度下的位移

应该指出的是，在这个振动模型中，摩擦力总是向右，其结果是摩擦力既做正功，也做负功。由于摩擦力大小不变，所以在一个周期里所做的净功为零，即在这种情况下，摩擦力起不到消耗振动能量的阻尼作用。(www.xing528.com)

综上所述，对于没有静、动摩擦之别的理想库仑摩擦力特性来说，如图1.35所示的系统不会发生自激振动。

现在，我们再来考查静摩擦和动摩擦不同的情况。

同样，假设传输带以恒定速度V转动，质量m与传输带之间的相对速度为v=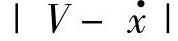。可以近似地认为，从静摩擦因数μ_s到动摩擦因数μ_d的变化过程与相对速度的大小呈线性变化关系，如图1.38的μ-v曲线所示。因此，作为相对速度的函数，摩擦因数可以近似地用式（1.94）表示（其中，静、动摩擦因数的差为Δμ=μ_s-μ_d）。

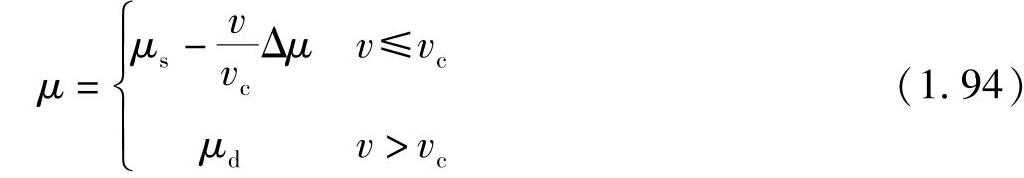
首先考查相对速度大于临界速度的情况（v＞v_c）。此时，μ=μ_d为一常数，无论物体是向左还是向右运动，摩擦力的大小都一样，始终向右。方程（1.89）可以写为

式（1.95）的一个显而易见的解为x=a，即质量处于静态平衡状态，不发生振动。即使在某种干扰下产生自由振动，实际中也会在不可避免的阻尼作用下衰减下去。也就是说，对于v＞v_c的情况，不会产生自激振动。

再来考查相对速度小于临界速度的情况（v＜v_c）。此时，摩擦因数是相对速度的函数。由于物体向左运动时的相对速度大于向右运动时的相对速度，所以，向左运动时的摩擦力小于向右运动时的摩擦力。把式（1.94）代入式（1.89），可得运动方程为

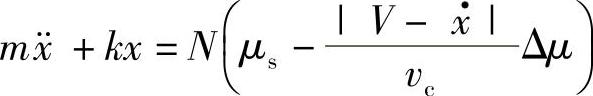
考虑到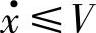的条件，进一步整理为

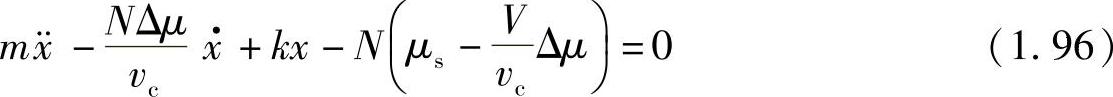
式（1.96）中，速度项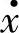前面的系数为负，相当于负的粘性阻尼，因此，该方程代表的是自激振动的情况。

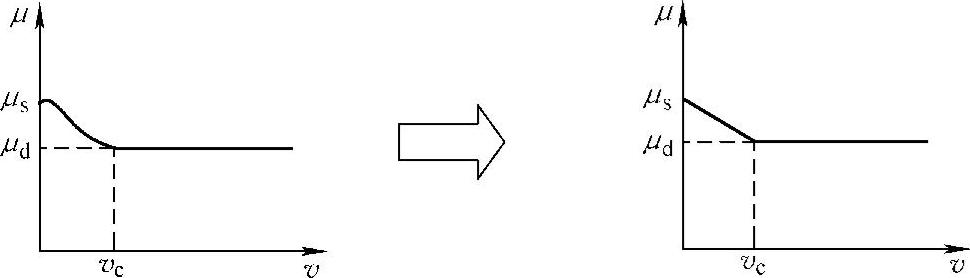
图1.38 摩擦因数的特性

可见，在相对速度从0增加到临界速度的过程中，摩擦因数由大变小的特性（μ-v曲线的负斜率特性）是等效负阻尼发生的根源。拉提琴时，通过改变V，时而使琴弦产生自激振动，时而使其产生自由振动，从而具有丰富的表达力。

令c_e=NΔμ/v_c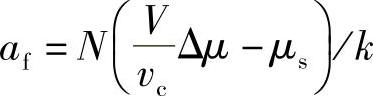，，式（1.96）变形为

进一步引入变量y=x+a_f，得

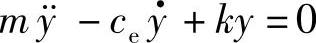
假设c_e满足欠阻尼的条件，方程（1.97）的解为

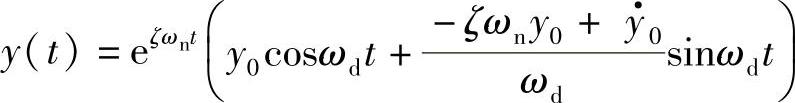
设初始条件为x₀=0、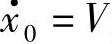，则有y₀=a_f、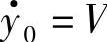，于是可得方程式（1.97）的解为

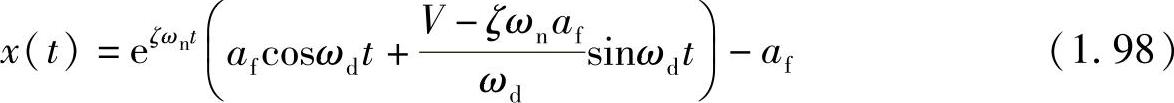
其中，，。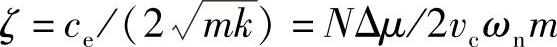

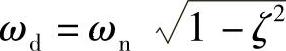作为一个计算举例，这里取f_n=100Hz，m=1kg，N=mg=9.8N，μ_s=0.3，μ_d=0.25，v_c=0.002m/s，V=0.1m/s，根据式（1.98）可以绘制出物体的位移响应，如图1.39所示。可见，这是一个振幅在短时间里迅速增大的不稳定响应。如图1.39b所示的位移-速度曲线为一个不断向外扩张的轨道。

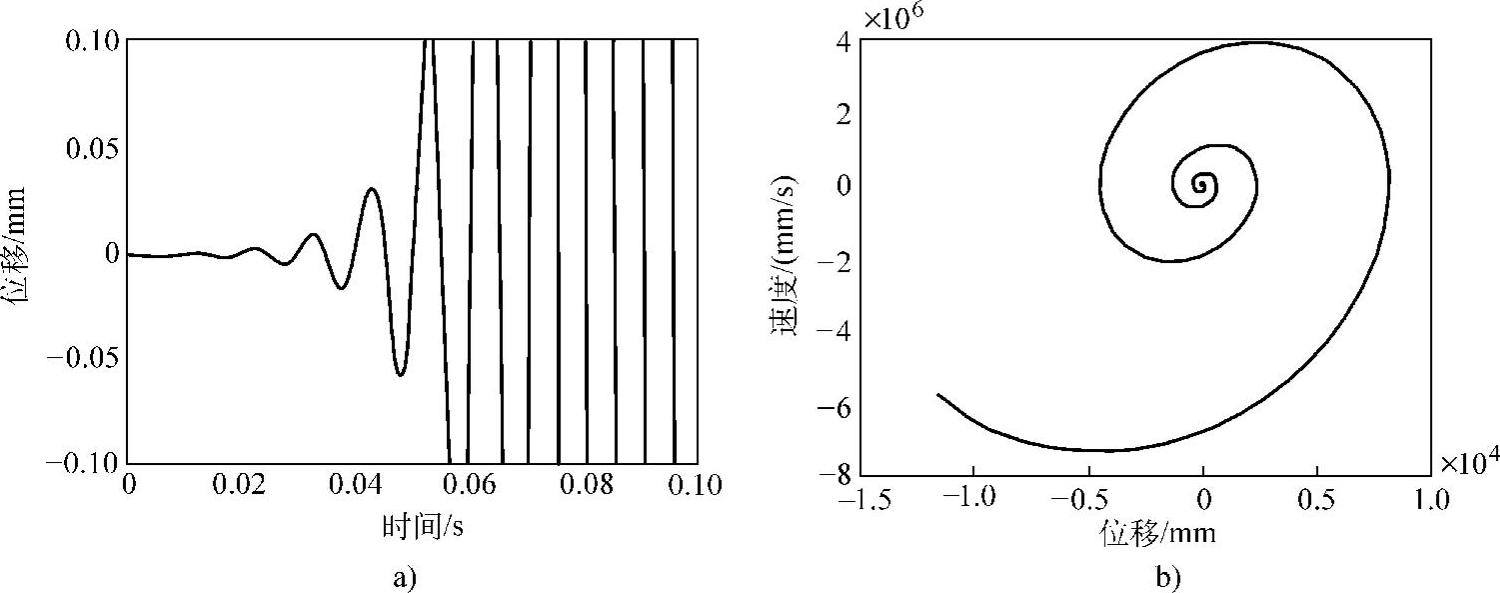
图1.39 处于自激振动状态的振动响应

a）位移响应 b）位移-速度响应曲线

这里，我们再次从摩擦力所做的功来考查这个现象。当物体向右运动时，运动方向与摩擦力同向，摩擦力做正功，设平均摩擦力为F⁺，振幅为x_a，则在向右运动的两个1/4周期里，摩擦力做的正功为W⁺=2x_aF⁺；当物体向左运动时，运动方向与摩擦力反向，摩擦力做负功，设此时的平均摩擦力为F^-，则在向左运动的两个1/4周期里，摩擦力做的负功为W^-=2xa F^-。由于向右运动时相对速度变小，摩擦因数变大；向左运动时相对速度变大，摩擦因数变小，因而有F⁺＞F^-，W⁺＞W^-。可见，在一个周期里，摩擦力所做的净功为正，即不断向系统补充能量，因此，系统的振动能量越来越大。

实际中，随着振幅的增加，必然会产生某种非线性效应而使振幅受到限制，加上不可避免的阻尼作用，自激振动的振幅不会无限增加，位移-速度响应曲线最终会收敛到一个封闭的极限轨道（Limit Cycle）上来。

应该指出的是，μ-v曲线具有负的斜率特性并不意味着肯定会发生自激振动。例如如果等效阻尼系数很大，以至于阻尼比大于1，则方程式（1.97）不存在简谐振动解；或者如果V很大，总是满足v＞v_c的条件，也不会发生自激振动。

此外，以上的讨论隐含了一个假定，即摩擦力始终向右，质量的振动不受传输带的影响。事实上，随着振幅的不断增加，振动速度也不断增加，总会到达V，在这个时候，质量将被传输带再次俘获而一起向右运动片刻，然后二者再分离。如此周而复始，形成一个Stick-Slip交替出现的振动现象。Stick的时间长短与传输带速度、静动摩擦力的大小及差值等因素有关。传输带速度越快，Stick的时间越短，Stick-Slip的周期也越短（即频率越大）。一般来说，这个Stick-Slip的最短周期由系统的固有周期所决定。

Stick-Slip振动需要用数值计算工具来求解。如图1.40所示为传输带匀加速运动时，用MSC.Adams得到的质量与传输带相对速度的计算结果。

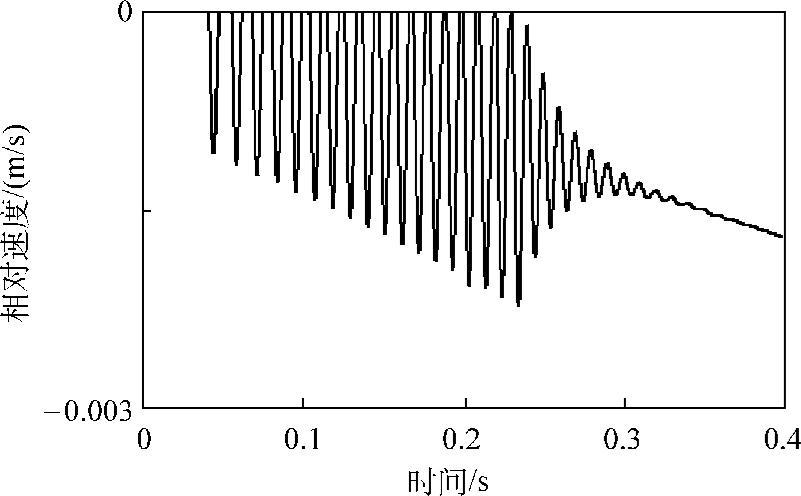
图1.40 质量与传输带的相对速度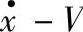（，单位：m/s）