如何提高机械振动系统稳定性并防止自激振动？

这里，我们来探讨系统具有什么样的特性时，会具有把运动能量转移为振动能量的能力。由于讨论的是系统本身的固有特性，可以使用自由振动的运动方程式（1.18）。

假设刚性变为负值，则运动方程可写为

令x=e^λt，λ为常数，称其为方程的特征值。代入方程式（1.84），可求得

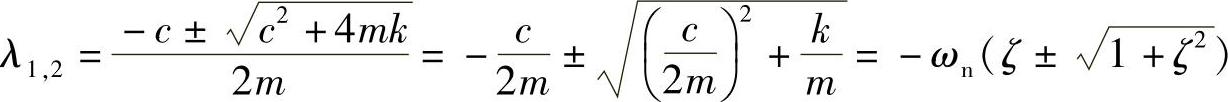
因此，可得2个特解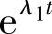、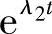。于是，该方程的通解为

其中，C₁、C₂为两个由初始条件确定的常数。假设初始条件为x（0）=x₀、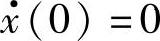，则由此条件可求得两个常数为

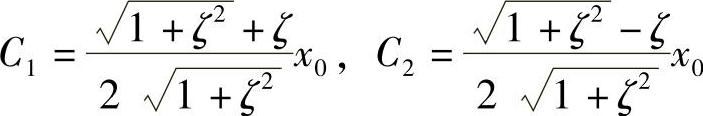
代入式（1.85）整理，可得位移响应为

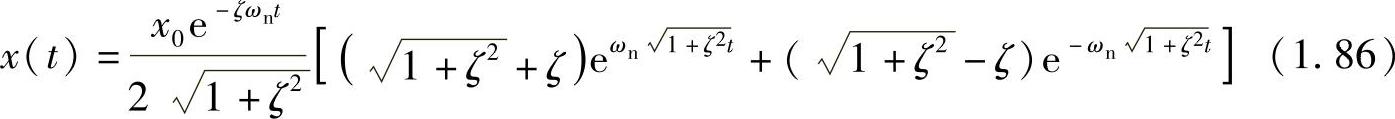
如图1.34a所示为ω_n=4π，ζ=0.05，x₀=1时的图像。显然，这不是一个振动响应。由此可知，负的刚性只会使物体越来越远离其平衡位置，这是一种不稳定的情况，称之为系统的静不稳定性。负刚性相当于系统具有负的特征值-ω²_n。

我们再来探讨阻尼为负的情况。此时，运动方程为(www.xing528.com)

将式（1.27）中的阻尼比改变符号，即可得以上方程的解为

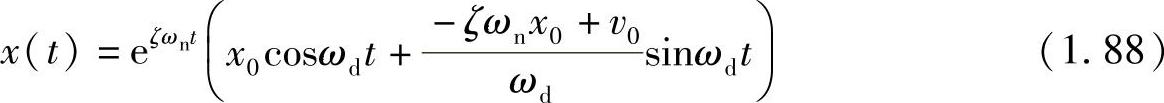
其中，。取ω_n=4π，ζ=0.05，x₀=1，v₀=0，上式的图像如图1.34b所示。可见，这是一个发散的振动现象，称之为系统的动不稳定性。

把方程式（1.87）变形为

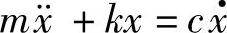
形式上，这相当于一个无阻尼系统在动态激励力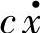作用下的强迫振动。由于这个激励力依存于振动本身，所以是一个自激振动。可见，系统具有负阻尼是自激振动发生的内在原因。由此可以推测，因为琴弓与琴弦之间存在负阻尼，拉提琴时才会把琴弓的一部分运动能量转移为琴弦的振动能量。

自激振动是一个动不稳定现象。需要说明的是，在讨论动稳定问题时，是以静稳定为前提条件的。换言之，对于静不稳定系统来说，讨论动稳定问题没有意义。关于稳定性问题，通常通过研究系统的特征值来判断。如果特征值λ是正实数，则由x=e^λt可知，随着时间的增加位移呈现单调增长趋势，为静不稳定；当特征值λ是负实数时，系统为静稳定。如果λ是复数，则可能涉及动不稳定问题。把特征值λ表示为λ=α+jβ，这里，α和β为实数。如果α≤0，β≠0，则为静稳定动稳定系统；如果α＞0，β≠0，则为静稳定动不稳定系统。有阻尼或无阻尼的自由振动系统就是一个典型的动稳定系统[见式（1.23）]。

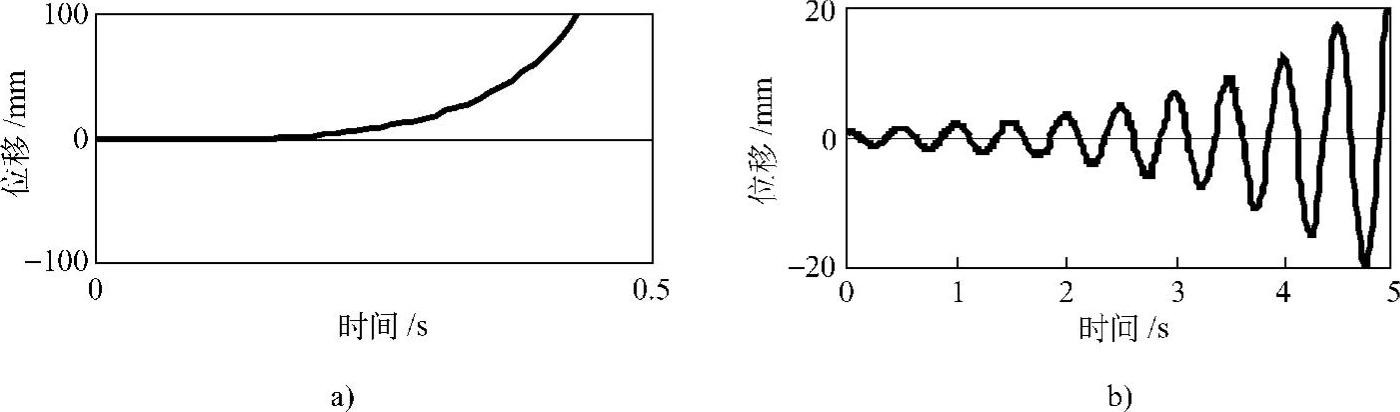
图1.34 单自由度系统的不稳定性

a）负刚性引起的静不稳定性 b）负阻尼引起的动不稳定性