在1.6.4版本下模拟典型冲击力对应的反应

作为拉氏变换的应用举例，本小节探讨单自由度系统在典型冲击力作用下的响应。

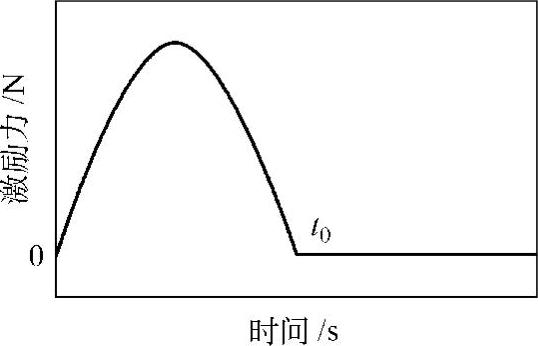
图1.28 正弦半波

1.正弦半波冲击力

考虑式（1.76）所示半个正弦波激励力的情况（参见图1.28）。

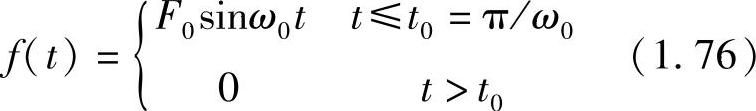
其拉氏变换为

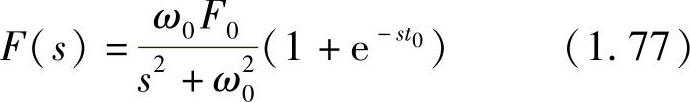
另一方面，系统的运动方程为

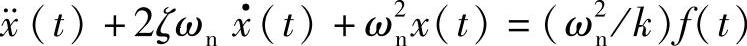
假设物体初始处于静止状态，对上式两边进行拉氏变换，可得

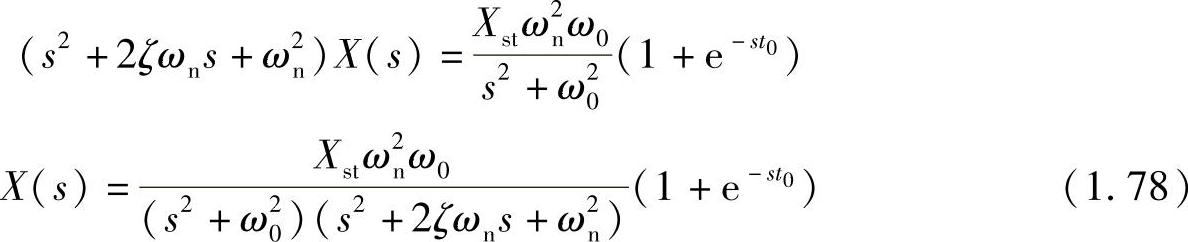
其中，X_st=F₀/k。对上式进行拉氏逆变换，即可得到时域响应。

为了便于应用拉氏逆变换，做以下变形

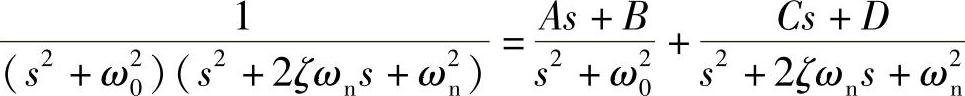
对上式右边进行整理，由方程两边分子的多项式的系数应该相等的条件，可得下列联立方程组

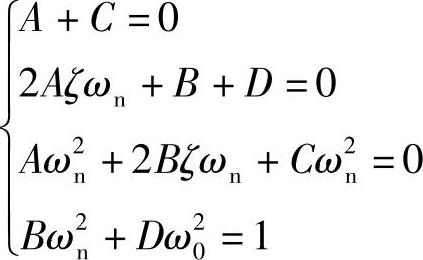
求解该方程组，可得待定常数A，B，C，D为

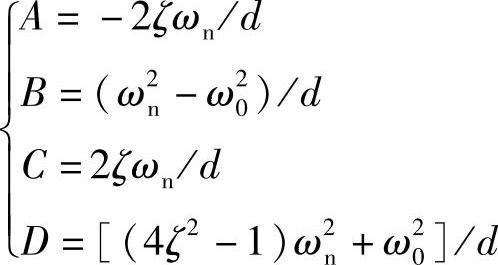
其中，d=（ω²_n-ω²₀）²+（2ζω_nω₀）²。

于是，应用拉氏逆变换公式，对式（1.78）做变换可得

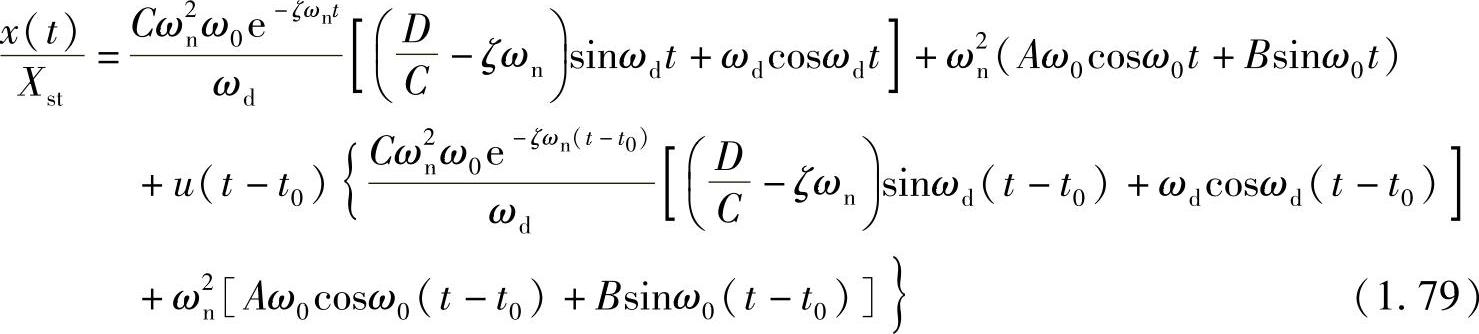
其中，，u为单位阶跃函数，。

由上式可知，静止的单自由度系统在正弦半波冲击力作用下的响应由两部分组成：一部分是从冲击力作用开始就产生的振动；另一部分是冲击力作用结束后发生的振动，这部分相当于把前者延迟时间t₀。二者的叠加即是总的响应。同时，在每部分响应中，又可以看到自由振动的成分（ω_d）和强迫振动的成分（ω₀）。

如图1.29所示为两种情况下振动响应随阻尼比变化的情况。横轴为正规化的时间，值为1的位置对应于正弦半波的结尾；纵轴为正规化的位移响应（x/X_st）。可见，当激励力的频率远小于系统的固有频率时（周期远大于固有周期），系统的响应主要发生在冲击力作用时间内（见图1.29b），冲击结束后，振幅迅速减小；反之，冲击力作用结束后，仍有可能发生较大的振幅（见图1.29a）。不论是哪种情况，增加阻尼可以有效地衰减掉冲击力结束后的振动。

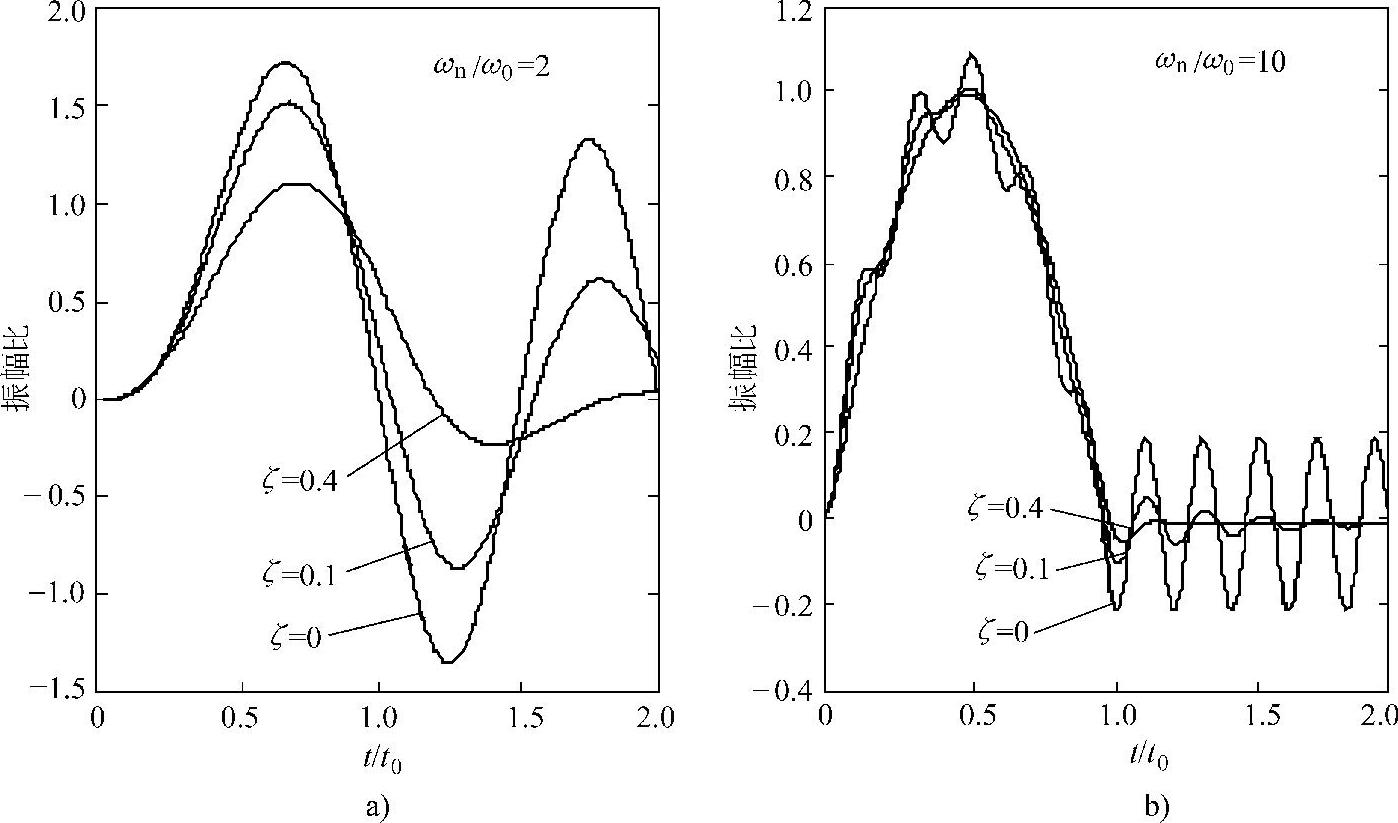
图1.29 系统固有频率为正弦半波外力频率的2倍和10倍时的响应

a）固有频率为正弦半波外力频率的2倍时的响应 b）固有频率为正弦半波外力频率的10倍时的响应(www.xing528.com)

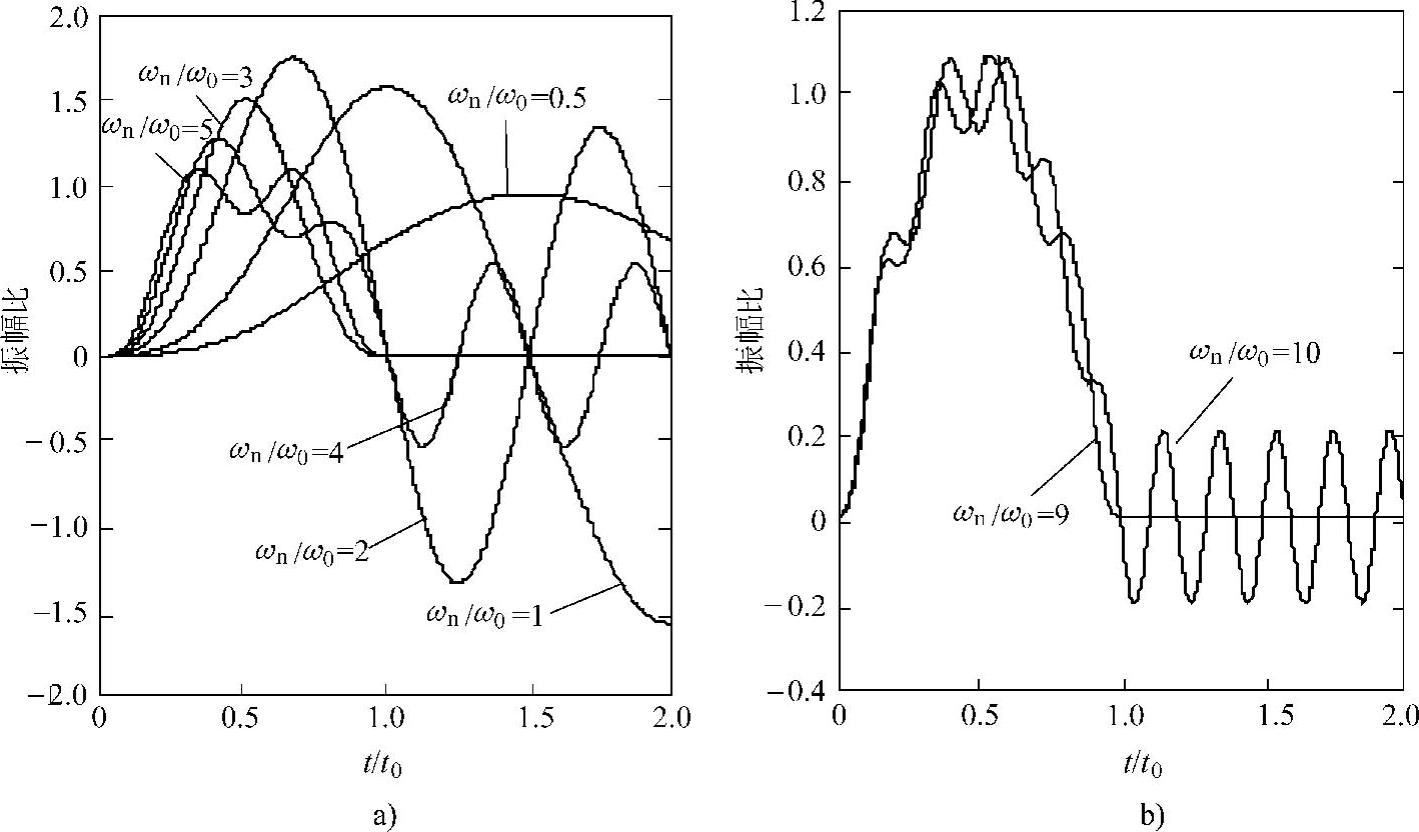
图1.30 无阻尼系统在正弦半波外力作用下的响应

a）响应示意图一 b）响应示意图二

如图1.30所示为在无阻尼的情况下，振动响应随正弦半波频率变化的情况。从图示的计算例子中可以看到一个特点，即当系统固有频率与正弦半波频率之比为3以上（包含3）的奇数时，冲击结束后的响应为0。这是一个很有趣的现象，据此，我们可以制定有效的减振措施。例如如果已知某种情况下，结构会受到近似于正弦半波的冲击力作用，则可以对结构进行优化设计，使得在冲击方向上最易被激起的模态的固有频率为正弦半波频率的3倍或以上的奇数倍，从而达到冲击后的余振迅速衰减的效果。

为了理解上述现象，我们来看看正弦半波函数所包含的频率成分。将s=jω代入式（1.77），可得正弦半波函数的傅里叶变换为

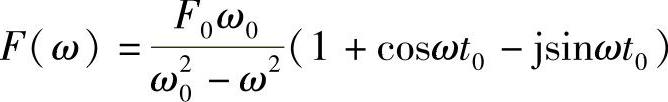
进一步可以求得激励力的自功率谱（Auto-power Spectrum）为

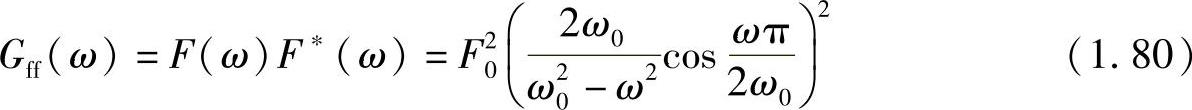
上式等于0的条件是ω=（2n+1）ω₀（n=1，2，3，…），即当ω=3ω₀，5ω₀，7ω₀，…时，G_ff（ω）=0。

如图1.31所示为根据式（1.80）绘制的正弦半波函数的自功率谱曲线（取F₀=1）。可见，在正弦半波频率（ω₀）的不为1的奇数倍上，正弦半波冲击力所具有的能量为0。因此，如果被冲击结构的固有频率与此重合，则自由振动不会被激起。

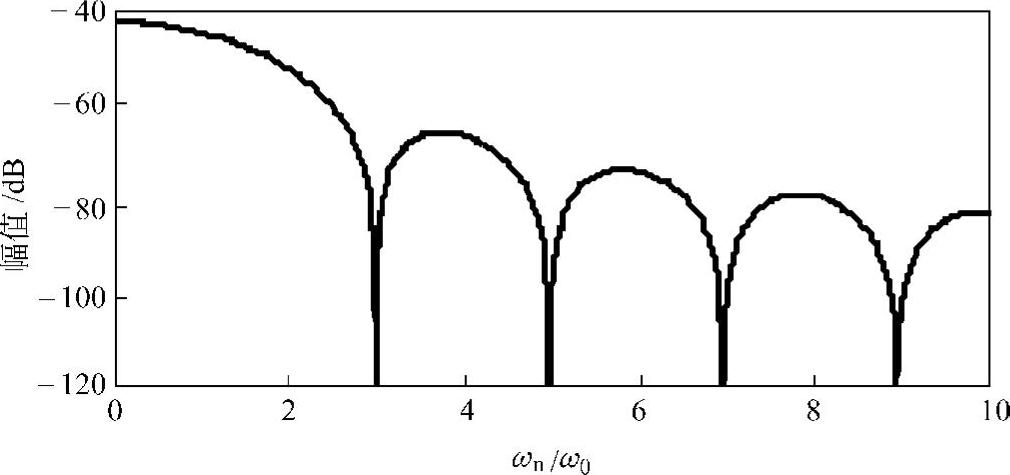
图1.31 正弦半波函数的自功率谱曲线

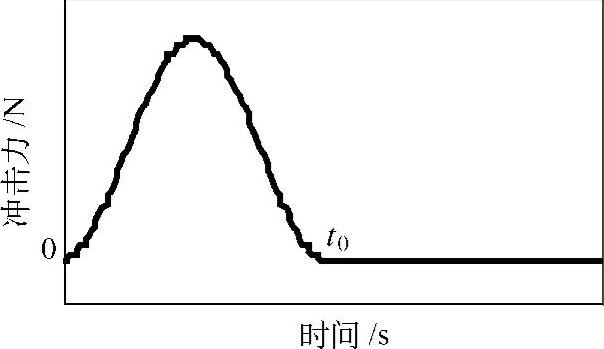
图1.32 汉宁函数

2.汉宁波冲击力

式（1.81）为汉宁函数（Hanning）的定义（参见图1.32）。相对于正弦半波函数，在开始及结尾的变化更为平缓。

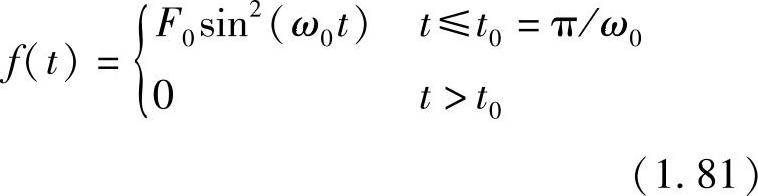
汉宁函数的拉氏变换为（取F₀=1）

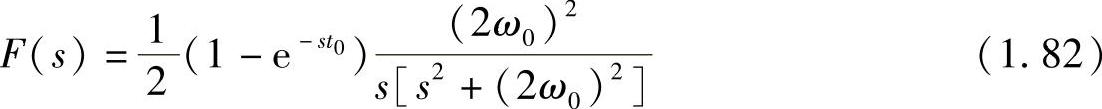
运用前面介绍的拉氏变换的方法，同样可以推导出在汉宁冲击力作用下系统的响应。由于推导繁杂，这里就不做介绍。需要指出的是，汉宁函数的傅里叶变换为

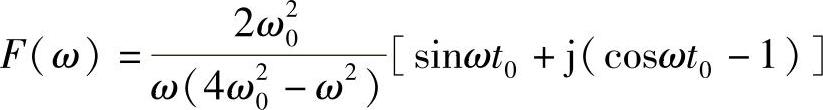
自功率谱为

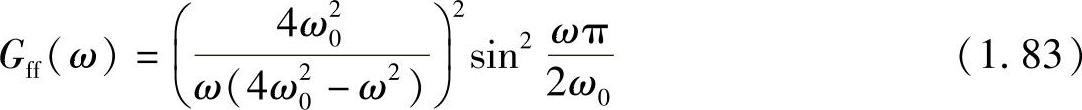
与正弦半波不同的是，在激励频率的不为2的偶数倍上，汉宁波冲击力所具有的能量为0。即当ω=2（n+1）ω₀（n=1，2，3，…）时，G_ff（ω）=0（参见图1.33）。

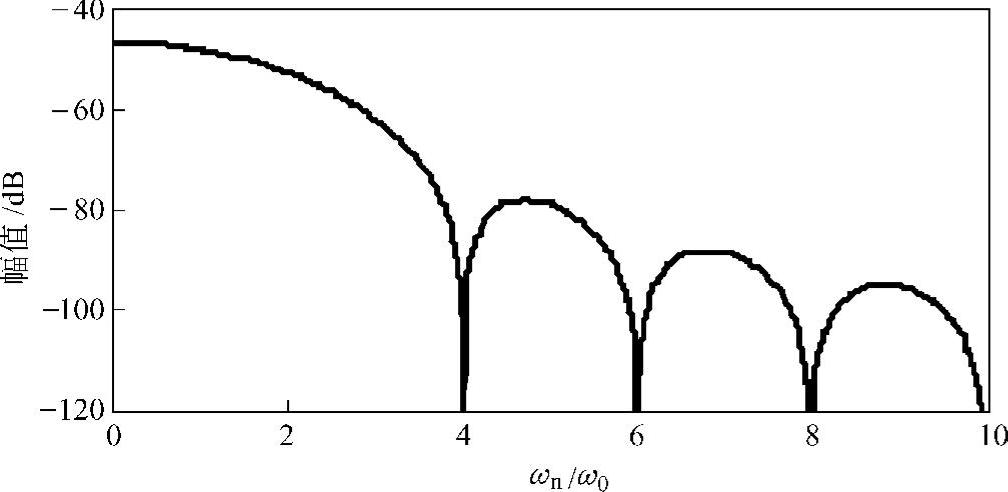
图1.33 汉宁函数的自功率谱曲线