应用拉普拉斯变换求解振动响应

本小节我们来介绍求解运动方程的拉普拉斯变换法（Laplace Transform）。首先，对拉普拉斯变换的定义及其主要性质做一下介绍。

在t≥0的领域上定义的函数f（t），其拉普拉斯变换定义为（简称拉氏变换）

其中，s=σ+jω为复数。如果用横轴代表实部，纵轴代表虚部，则所有s的取值构成一个复平面，通常称为[s]平面。由于e^-st=e^-σte^-jωt，相当于一个角频率为ω的简谐振动e^-jωt被指数函数e^-σt所衰减，所以σ相当于阻尼作用（参照图1.12）。如果σ＜0，则e^-σt随着时间的增加越来越大，上述积分可能不存在。通常来说，存在一个实常数σ_c，在σ＞σ_c的领域上，式（1.72）所示的积分存在，σ＞σ_c称为F（s）的收敛域。相反，σ＜σ_c的s称为F（s）的特异点（s_p）。

与式（1.72）相对应，拉普拉斯逆变换定义为

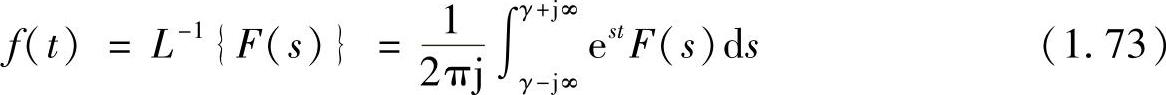
其中，γ为实常数，并且满足γ＞Re（s_p）。如果所有的特异点处于复平面的左半边，即，Re（s_p）＜0，则可取γ=0。此时，式（1.73）与傅里叶逆变换等价。上式所代表的积分又称Bromwich积分。

在应用拉氏变换及其逆变换时，通常并没必要直接用式（1.72）或式（1.73）求解，而可利用大量已知的变换关系。

我们知道，在把时域信号转换到频域进行分析时，常用傅里叶变换（Fourier Transform）。傅里叶变换是把（-∞，∞）上的时间信号转化为（-∞，∞）上的频率成分，如下式所示

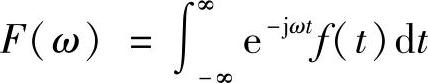
上式的成立条件是|f（t）|在（-∞，∞）上的积分存在；拉氏变换则是把（0，∞）上的时间信号转化为[s]平面上的成分分布。对比二者的定义可知，拉氏变换相当于给原有的函数乘上一个衰减指数，然后只在（0，∞）上做傅里叶变换，因而大大地缓和了傅里叶变换成立的条件。正是由于拉氏变换所具有的一些性质，使得它在求解微积分方程及其工程应用方面，尤其是在动力学、控制工程、电气技术等领域得到了广泛的应用。以下不加证明地给出拉氏变换的一些基本性质和定理，并且在表1.3中列出一些求解振动问题常用的拉氏（逆）变换对。

表1.3 常用的拉氏（逆）变换关系

（续）

1.线性叠加性

设a₁，a₂，…，a_n为常数，F₁（s），…，F_n（s）分别为f₁（t），…，f_n（t）的拉氏变换，则有

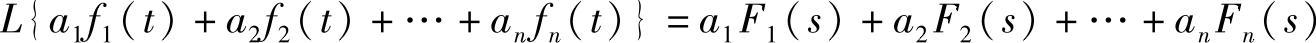
2.移位性

设F（s）为f（t）的拉氏变换，则f（t-τ）的拉氏变换为

L{f（t-τ）}=e^-τsF（s）

另一方面，e^τsf（t）的拉氏变换为

L{e^τsf（t）}=F（s-τ）

3.微积分的拉氏变换

设F（s）为f（t）的拉氏变换，则微分f′（t）、f″（t）的拉氏变换分别为

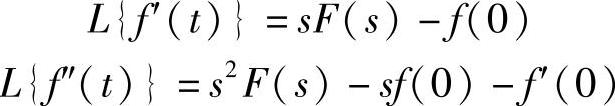
积分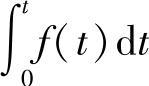的拉氏变换为

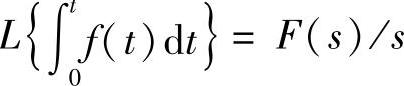
可见，通过拉氏变换，可以把微分和积分运算分别转换为关于s的乘法和除法的代数运算，因而在求解微积分方程方面被广泛应用。

4.卷积的拉氏变换

函数f（t）和g（t）的卷积（Convolution Integral）定义为(www.xing528.com)

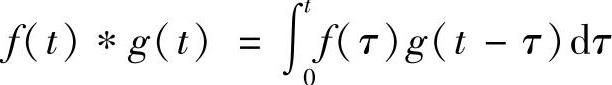
它的拉氏变换为

L{f（t）∗g（t）}=F（s）G（s）

即两个函数的卷积的拉氏变换等于各个函数的拉氏变换的乘积。

以下运用拉氏变换的方法，来求解有粘性阻尼的单自由度系统在任意力作用下的时间响应。首先，将方程（1.64）变形为

对上式两边进行拉氏变换，可得

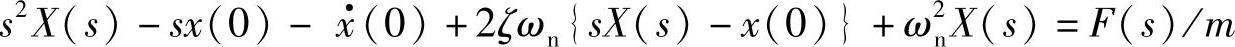
其中，X（s）为位移x（t）的拉氏变换，F（s）为作用力f（t）的拉氏变换。将上式整理后，可得

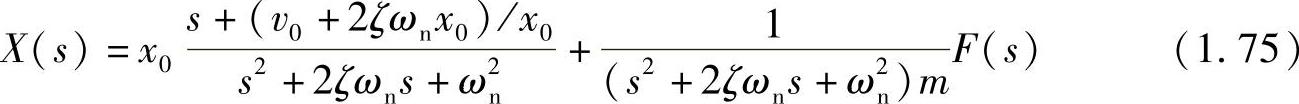
式（1.75）右边第一项是由初始条件引起的自由振动，第二项为外力激励的强迫振动。对式（1.75）作拉氏逆变换，即可得到时域上的响应。

先来看第一项的拉氏逆变换。将分母通过因式分解变形为（其中，ω_d=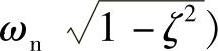

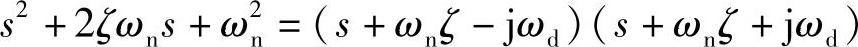
应用拉氏逆变换公式

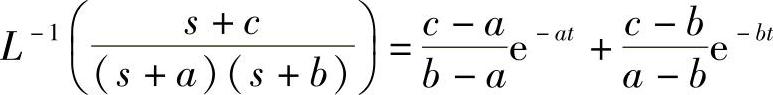
可以求得式（1.75）右边第一项的拉氏逆变换为（略去繁杂的整理步骤）

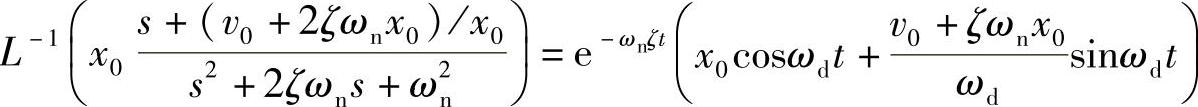
现在，再来看式（1.75）右边第二项的拉氏逆变换。这一项由两个拉氏变换函数的乘积构成，因此其逆变换应为一个卷积形式。令

应用拉氏逆变换公式

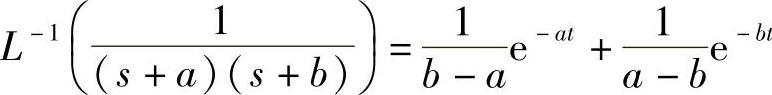
容易求得

再应用卷积的拉氏变换关系，可得

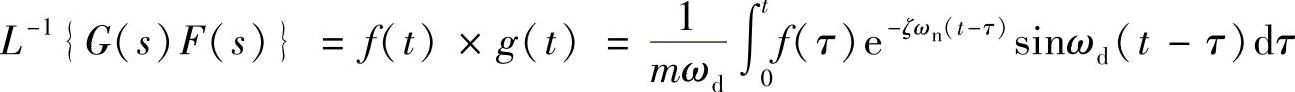
因此，由式（1.75）的拉氏逆变换，可得与式（1.71）所示结果相同的位移响应

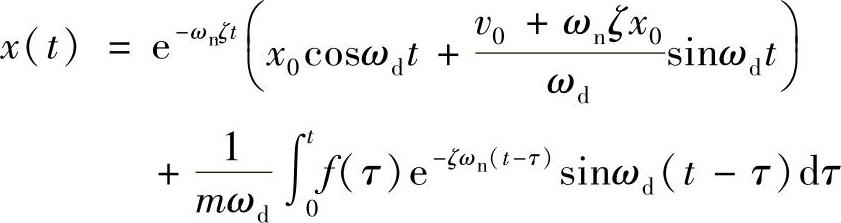
对于初始条件为0的情况，上式变为式（1.70）。即使初始条件不为0，由于阻尼的作用，上式第一项的自由振动成分也会很快衰减掉。

由以上推导过程可见，拉氏变换是求解复杂的振动响应问题的强有力的工具。如果用傅里叶变换求解微分方程，则只能得到不受初始条件影响的稳态解（相当于方程的特解）；而应用拉氏变换，则可以得到由瞬态响应与稳态响应构成的方程的通解。