库仑摩擦的等效粘性阻尼近似方法

由上节可知，求解具有干摩擦系统的振动响应的确是件困难的工作。这里，我们介绍利用等价粘性阻尼来近似表现库仑摩擦的方法。

我们已知，摩擦力在一个周期消耗的能量为4Fx₀，而粘性阻尼力在一个周期消耗的能量为πCωx²₀。利用摩擦力耗能与粘性阻尼力耗能相等的假定，可以确定出等价的粘性阻尼系数为

等价粘性阻尼比为

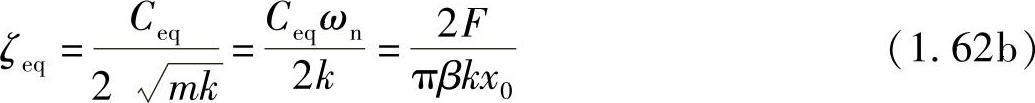
图1.25 用等价粘性阻尼近似得到的干摩擦系统的强迫振动的幅频特性

在1.3.3小节，我们已经求出了粘性阻尼系统稳态强迫振动的响应为(www.xing528.com)

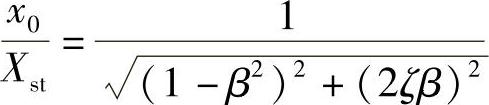
将式（1.62b）代入上式整理，可得

显然，上式在F/P＜π/4时有实际意义。图1.25是根据式（1.63）计算出来的结果，与图1.23对比，在接近共振的领域，用等价粘性阻尼的方法可以较好地近似原系统的振幅。由于实际中人们更关心共振时的情况，因此，式（1.63）所代表的近似方法具有实际应用意义。

最后需要指出的是，如图1.19b所示的摩擦特性是在摩擦因数一定的理想状态的情况下。实际中，摩擦因数会受到相对滑动速度、温度、湿度、正压力的大小等因素的影响而发生变化，例如相对滑动速度为零时，静摩擦因数μ_s一般大于滑动开始后的动摩擦因数μ_d。此外，当运动方向改变时，摩擦力方向的突然反转在数学上是一个不连续函数，这会引起数值解析的极大困难。因此，在摩擦力的模型化中，通常引入一个微小的速度域值v_s，在（-v_s，v_s）的领域内，设摩擦因数线性变化，以保持连续性。这样建模的摩擦因数的特性曲线如图1.26所示（简称μ-v曲线）。

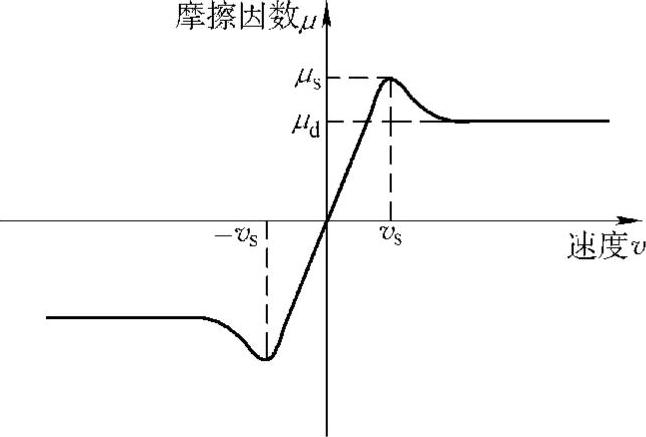
图1.26 解析实践中常用的摩擦 因数建模方法（μ-v曲线）