求解具有库仑摩擦的系统在外力作用下的强迫振动是一个困难的工作。这是由于当外力与弹性回复力以及惯性力的和小于摩擦力时,物体会停滞下来;当外力与弹性回复力的和大于摩擦力时,物体又开始运动。由于存在这种非线性特性(Stick-Slip),即使对于单自由度系统在简谐外力作用下的最简单情况,也不容易给出完整的解析解。1931年,Den Hartog推导出了在不存在停滞的情况下(Non-Stop Motion)以及每半周期上停滞一次的情况下(One Stop Per Half Cycle)的振幅与摩擦力大小的关系。这里,我们对其结果做以下介绍。
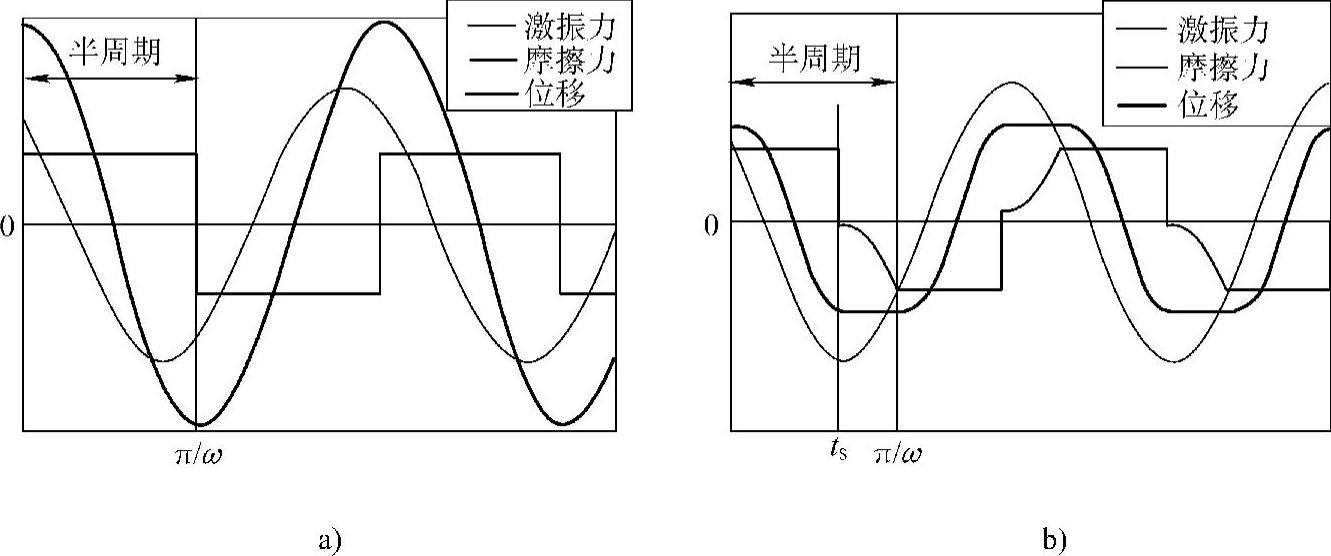
图1.21 库仑摩擦阻尼系统的稳态强迫振动
a)不存在停滞的运动情况 b)每半周期停滞一次的运动情况
首先考虑不存在停滞的情况下的稳态振动(见图1.21a)。摩擦力的大小为F,这里,激励力表示为p=Pcos(ωt+φ),运动方程为

参照图1.19,假设物体处于最右端的时刻为考查的起始点(此时振幅为最大,设为x0),则在第一个半周期上,物体由右向左运动,速度为负,式(1.54)摩擦力前取负号。运动方程为
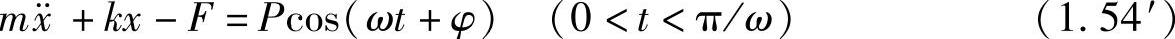
引入参数a=F/k,Xst=P/k,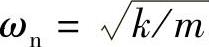 ,并令y=x-a,式(1.54′)可变形为
,并令y=x-a,式(1.54′)可变形为
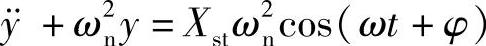
设该方程式的特解为y=y0 cos(ωt+φ),代入上式可求得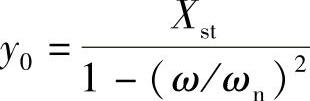 ,于是通
,于是通
解为
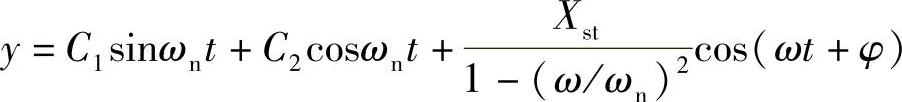
C1、C2为待定常数,进一步可得
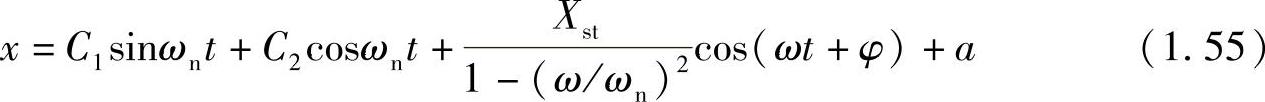
式(1.55)在0<t<π/ω的半个周期上成立,常数C1、C2由边界条件决定。考虑t=0时的边界条件x(0)=x0,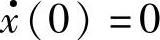 ,可以求得C1=XstβBsinφ,C2=x0-a-XstBcosφ
,可以求得C1=XstβBsinφ,C2=x0-a-XstBcosφ
其中,β=ω/ωn,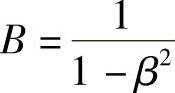 。代入式(1.55),可得位移为
。代入式(1.55),可得位移为
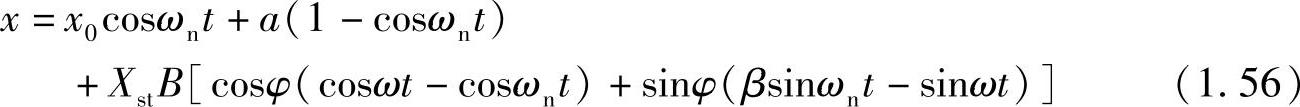
但是,这个解中还有两个未知数x0、φ。这里,再次运用t=π/ω时的边界条件,x(π/ω)=-x0,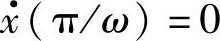 ,可以求得x0、φ。这里略去推导细节,只给出以下结果
,可以求得x0、φ。这里略去推导细节,只给出以下结果
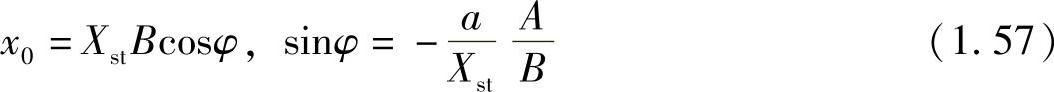
其中,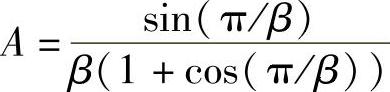 。可见,即使可以确定式(1.56)中的未知数x0、φ,这个解的形式也非常复杂。
。可见,即使可以确定式(1.56)中的未知数x0、φ,这个解的形式也非常复杂。
这里,我们不去深究式(1.56)所代表的位移在每个时刻的值,而是重点考查其振幅x0。由式(1.57)可得
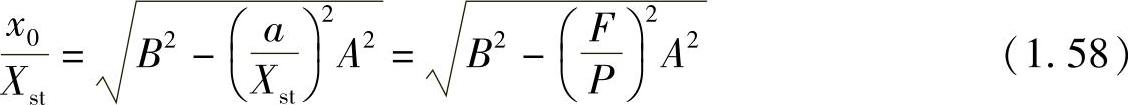
可见,振幅大小除了与频率有关外(A、B均为频率的函数),还与摩擦力与激励力的幅值之比有关。上式虽然是在半个周期上推导出来的,对于稳态振动来说,这个振幅特性也适合于其他时间段。显然,当(F/P)2>>(B/A)2时,上式根号下为负,这个结果不再成立。这时,“不存在停滞”的假定也不再成立,在运动途中会出现停滞片刻的现象。(https://www.xing528.com)
考虑每半个周期停滞一次的情况(见图1.21b)。对于没有停滞的时间段(0,ts),式(1.56)依然成立,并且有边界条件
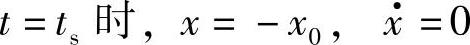
另外,对于停止状态(t=0),有以下力的平衡关系(惯性力为0)
-kx0+F+Pcosφ=0 (1.59)由t=ts的边界条件,可得两个含有三个未知数(x0,φ,ts)的方程。把这两个方程式与式(1.59)联立,可以推导出以下关系式
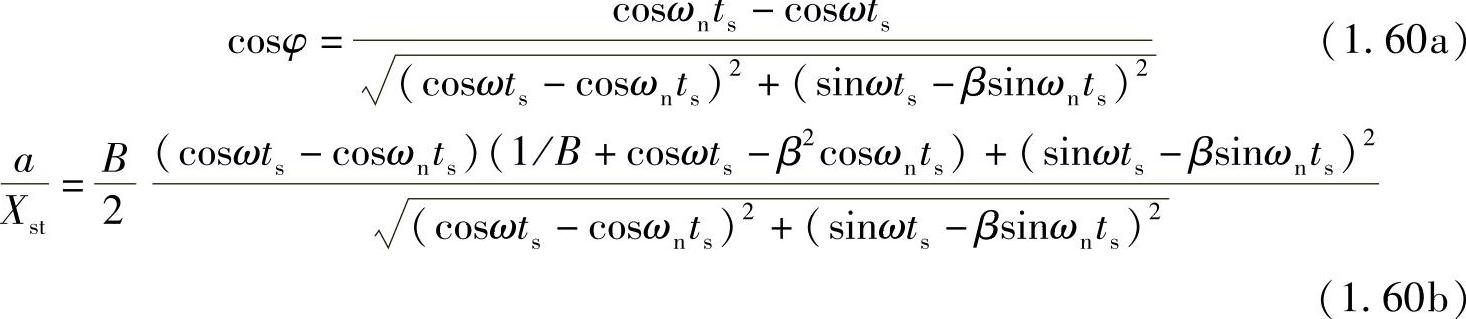
式(1.60b)实际上给出了在摩擦力与激振力已知的情况下,决定停滞发生时刻(ts)的方法。可是遗憾的是,这个方程无法直接求解。因此,由式(1.60b)求得ts,代入式(1.60a)求得cosφ,然后再由式(1.59)求得x0的办法行不通。
在此,通过在区间(0,π/ω)上对ts取一系列离散值的办法来进行数值计算。例如对于β=ω/ωn=0.5,根据式(1.60)可以算出a/Xst及cosφ随ωts变化的曲线,进一步通过对关系式(1.59)变形,可得x0/Xst随ωts变化的曲线,如图1.22所示。
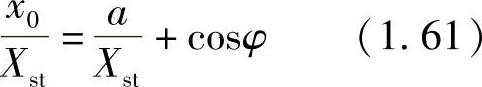
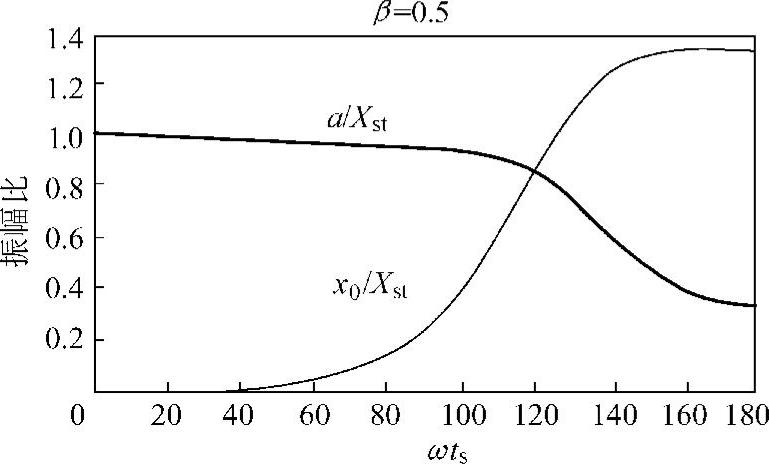
图1.22 数值计算举例
当给定摩擦力与激励力的比值时(F/P=a/Xst),由如图1.22所示的曲线,即可找到对应的振幅(x0/Xst)。
用这样的计算方法以及公式(1.58)和式(1.61),可以求出在给定摩擦力与激励力比值的条件下的振幅倍率。如图1.23所示为利用现代计算工具(Excel)得到的结果。该结果有一个显著的特点,就是F/P存在一个临界值π/4。当F/P<π/4时,由式(1.58)可知,共振时(β=ω/ωn=1),x0/Xst→∞,这对于满足F/P<π/4的所有摩擦力都成立。我们知道,对于粘性阻尼系统,共振时振幅为一有限值,不可能成为无限大;而干摩擦阻尼系统却不同,共振时振幅变为无限大。
为了理解这个结论,我们来比较激励力所做的功和摩擦力所做的功。共振时,激励力在一个周期里所做的功由式(1.38)可得
WP=Px0 π
而摩擦力所做的功为
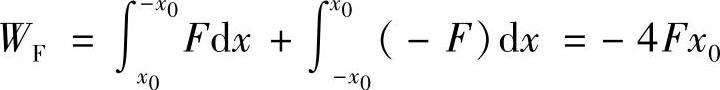
激励力做正功,给系统输入能量;而摩擦力做负功,消耗系统的能量。二者的大小都与振幅的一次方成正比。显然,当F/P<π/4时,摩擦力所消耗的能量小于激励力所供给的能量。因此,系统的能量不断增加,振幅越来越大(图1.23中,标注π/4的曲线实际上是F/P=0.785<π/4的情况)。
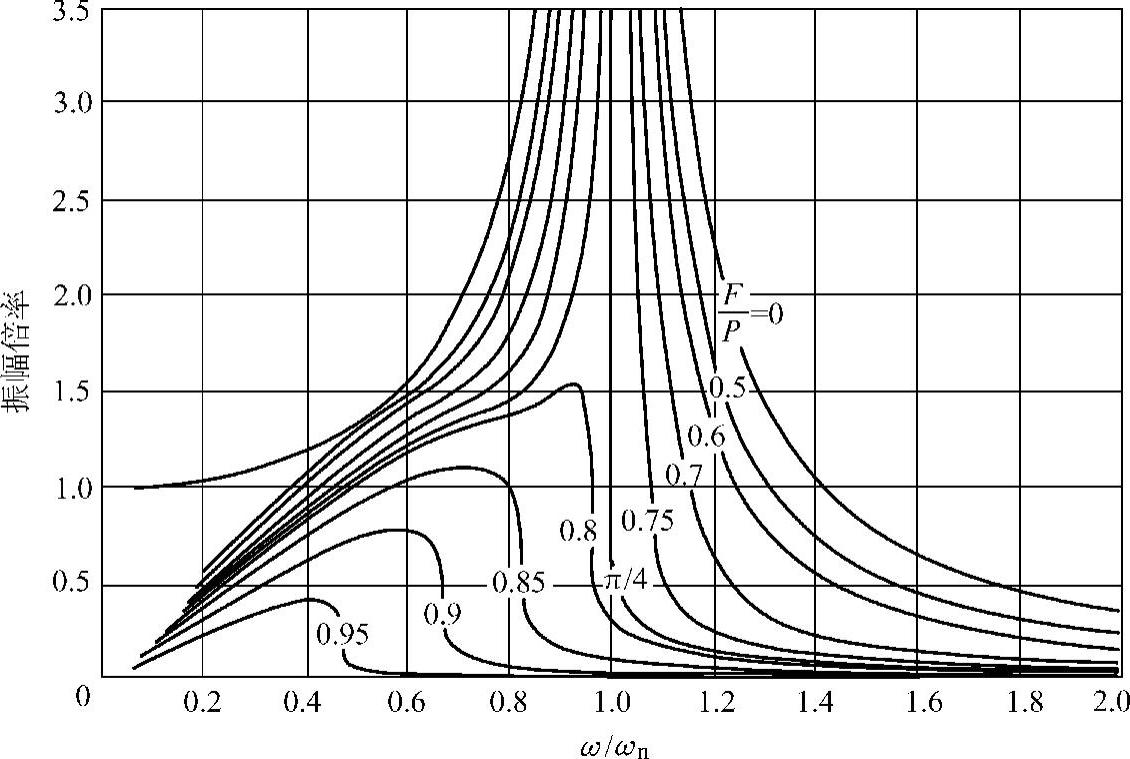
图1.23 具有库仑摩擦阻尼的系统的强迫振动的幅频特性
粘性阻尼力所做的功的大小与振幅的二次方成正比。不管阻尼多小,消耗的能量最终会与供给的能量达到平衡,因而振动能量及振幅不会无限增加。
另外,图1.23中左下角的三角部位为空白,对应于每半周期停滞两次及以上的情况。对于这种复杂的情况,尚且无法得到理论解。利用商业机构解析软件可以求解到这个部位的结果,但由于振幅很小,无关紧要,这里不予介绍。作为参考,图1.24给出每半周期停滞3次时的位移及速度的特征(这个结果是在F/P=0.5、β=0.1的情况下,用商业机构解析软件MSC.Adams计算得到的)。
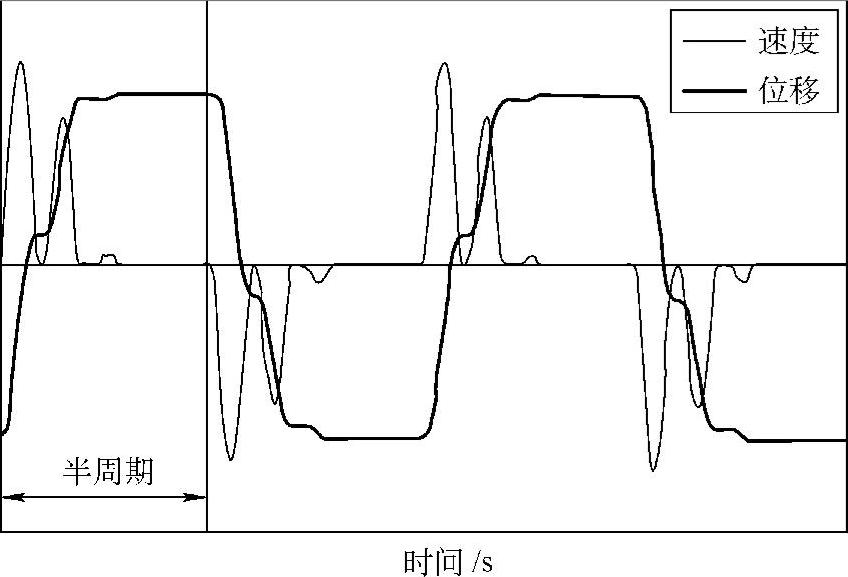
图1.24 每半周期停滞3次时的位移及速度的特征
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




