下面从外力做功与振动能量的关系的角度,考查强迫振动频率响应的特征。
1.无阻尼的情况
对于无阻尼系统,在固有频率以外,激励力与位移要么同相,要么逆相(见图1.6)。由式(1.38)可知,这时在一个周期里外力所做的功为0。根据激励力频率的大小,可以分为小于固有频率、等于固有频率和大于固有频率三种情况。
1)当ω<ωn时,ψ=0,在第一个1/4周期里外力所做的功为
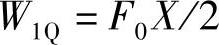
t=0时,动能TE和弹性势能UE分别为(x=Xsinωt, )
)
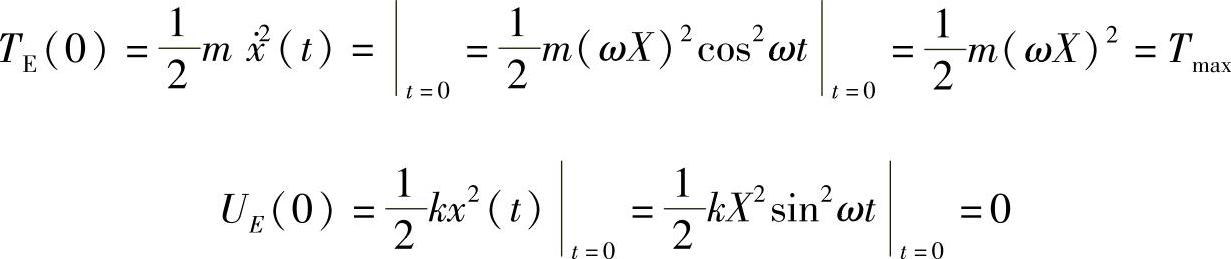
即动能为最大,势能为0。而当t=T/4时(T为周期),动能为0,弹性势能为最大,表示为

根据式(1.37),可得(无阻尼的情况,D=0)

由上式可知,如果没有外力做功,W1Q=0,最大动能等于最大势能;在有外力做功的情况下,最大动能不等于最大势能。对于这里所讨论的情况(ω<ωn),在位移由0增加到最大的第一个1/4周期里,外力做正功,势能由0变为最大,Umax=W1Q+Tmax。即除了由动能转化来的部分以外,外力所做的正功也转变为弹性势能而储存起来。因此,最大势能大于最大动能。
同样,考查在第二个1/4周期的情况,可得以下关系

上式表明,在位移由最大降到0的第二个1/4周期里,势能并没有全部转化为动能,其中一部分用于对外力做功(外力做负功),即在第一个1/4周期里由外力做正功而储存起来的弹性势能在第二个1/4周期里通过对外力做功而释放出来。“最大势能大于最大动能”的特点依然保持。
第三个1/4周期与第一个1/4周期相同,第四个1/4周期与第二个1/4周期相同。
可见,外力做功的过程与系统势能的储存与释放相对应。由于能量守恒,储藏的能量与释放的能量完全相等,一正一负,总的功为零。这意味着没有振动能量转变为热能消耗掉,振幅为一定。由式(1.39)或式(1.40)很容易求得振幅为
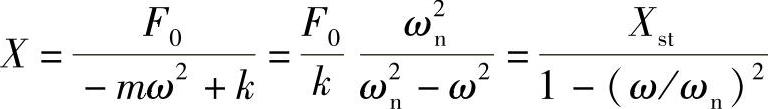
这与1.2.2节中通过求解运动方程得到的结果一致。
2)当ω=ωn时,ψ=π/2,外力在每个1/4周期里都做正功,可得
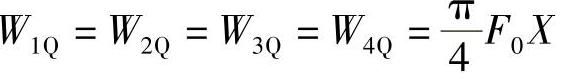
在第一个1/4周期与第二个1/4周期里,分别有关系式
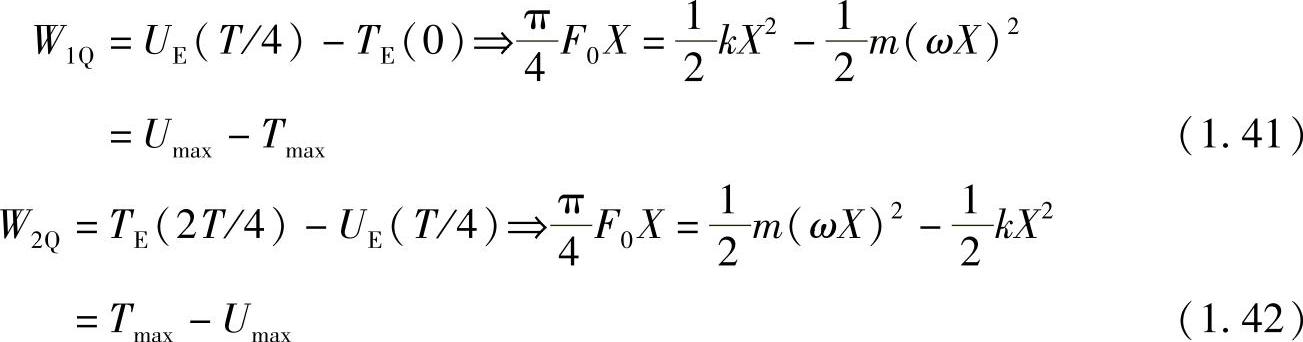
式(1.41)表明,外力所做的正功等于相对于最大势能的增加量。即在第一个1/4周期里,外力所做的功变为弹性势能,最大势能大于最大动能。而式(1.42)表明,外力所做的正功等于(相对于第一个1/4周期末的最大势能)动能的增加量,即在第二个1/4周期里,外力所做的功变为系统的动能,最大动能大于最大势能。如此周而反复,动能和势能越来越大,振幅也越来越大(见图1.5)。
3)当ω>ωn时,ψ=π,外力在第一个1/4周期里做负功,W1Q=-F0X/2,利用同样的分析方法,可以得到以下能量关系(https://www.xing528.com)

可见,此时有最大动能大于最大势能的特点。在这个1/4周期里,物体通过惯性对外力做功,从而释放出一部分动能;而在第二个1/4周期里,外力做正功,所做的功转化为动能的增加,此时的能量关系为
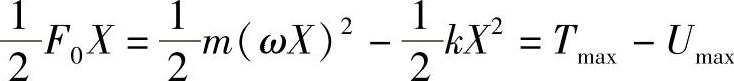
最大动能大于最大势能的特点依然成立。可见,当ω>ωn时,外力做功与动能的储存与释放相对应,在一个周期里外力所做的功之和为0,振动的振幅为一定。
2.有阻尼的情况
以上通过对无阻尼系统的能量分析,我们掌握了外力的作用与共振的关系。对于有阻尼系统,也可以进行同样的分析。
由式(1.13)可知,在每个1/4周期里粘性阻尼所消耗的能量为
D=cπωX2/4
在第一个1/4周期里,根据式(1.37)可得关系式
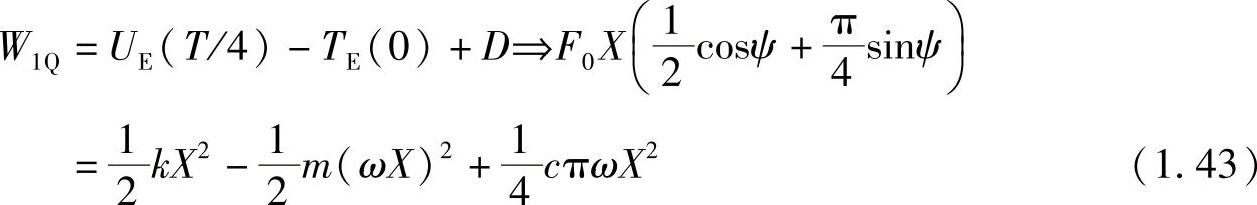
同样,在第二个1/4周期里,有

把式(1.43)与式(1.44)相加,可得
πF0Xsinψ=cπωX2 (1.45)式(1.45)左边代表外力在一个周期里所做的功[见式(1.38)],右边代表阻尼力所消耗的能量[见式(1.13)]。因此,在稳态强迫振动中,外力所做的功等于阻尼所消耗掉的能量(通过阻尼力做功而转化为热能)。
把式(1.43)与式(1.44)相减,可得

当ω<ωn时,由图1.16可知,相位角在(-π/2,0)的区间上,cosψ>0,因此有最大势能大于最大动能的特点;当ω>ωn时,相位角在(-π,-π/2)的区间上,cosψ<0,因此有最大动能大于最大势能的特点;当ω=ωn时,ψ=π/2,cosψ=0,最大动能等于最大势能,即共振时,动能与势能之间实现等值转化,不像无阻尼的情况那样不断增加。这是有粘性阻尼的系统共振时的重要特征。由式(1.45)可知,共振振幅为一个有限值

容易证明,式(1.47)与式(1.32)等价。另外,联立式(1.45)与式(1.46),可求得振幅X和相位ψ,结果与式(1.30′)相同。
需要说明的是,对于共振以外的情况(ω<ωn或ω>ωn),可以把激励力分解为与位移同相的部分和直交的部分。前者一个周期里的做功为0,其做功过程与势能或动能的储藏与释放相对应;后者一周期上做功大于0,其值等于阻尼耗能,即这部分功转化成了热能消耗掉。
以上考查结果归纳在表1.2中。
表1.2 强迫振动的特征总结
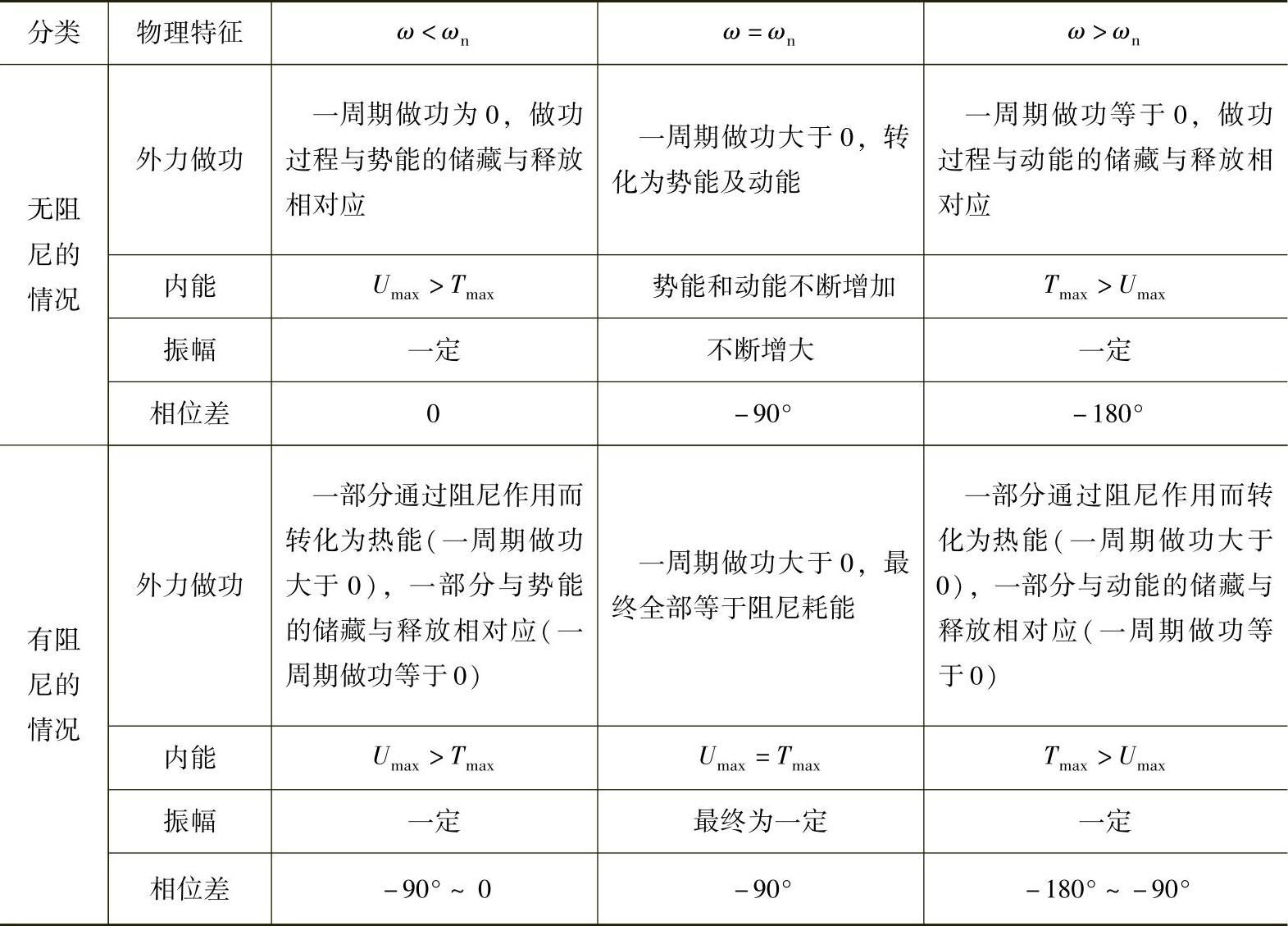
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




