外力做功与振动能量的关系探究

如图1.9所示系统中，弹性力和阻尼力代表系统的内力，激励力为外力。根据热力学第一定律，外力所做的功减去消耗掉的能量等于系统内能的变化量，即

W=ΔE+D （1.37）

W为外力在加载过程（从t₁时刻到t₂时刻）中所做的功，D为由阻尼消耗掉的能量（转化为热能），ΔE为内能的变化量（内能=动能+势能）。

首先考查外力F（t）=F₀sin（ωt+ψ）作用在做简谐振动x=Xsinωt的物体上时所做的功。取位移为0的某时刻为起始时刻（t=0），我们来看在一个周期内（T=2π/ω）外力所做的功。为了便于理解，我们把一个周期等分为4段，分别用1Q、2Q、3Q、4Q表示。在第一个1/4周期里，外力所做的功为

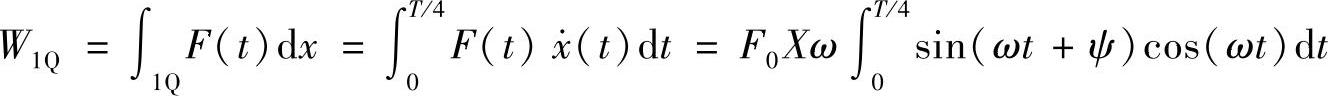
将sin（ωt+ψ）=sinωtcosψ+cosωtsinψ代入，并应用积分公式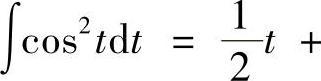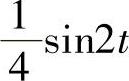进行运算，可得上式的结果为

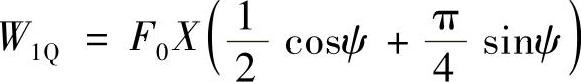
同样，可以求得2Q、3Q、4Q的结果分别为(www.xing528.com)

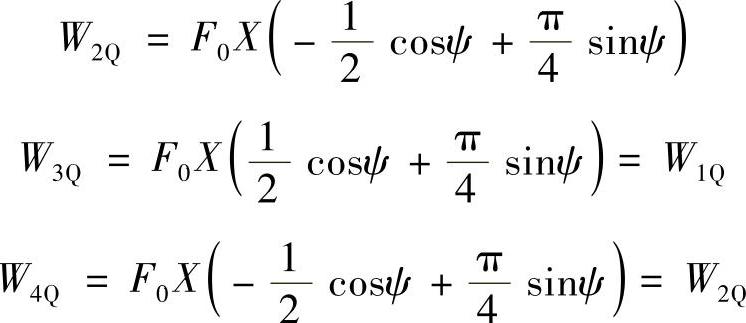
在整个周期上所做的功为

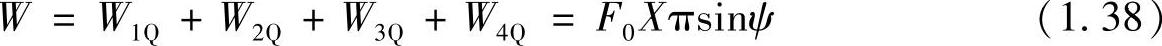
这个结果与激励力和位移响应的相位差ψ有关。当ψ=0时，W=0，即外力所做的功为0；当ψ=90°时，做功最大，为W=F₀Xπ。由此，我们得到一个重要的结论：

当一个简谐激励力作用在以相同频率做简谐振动的物体上时，如果这个力与位移同相或反相，则在一个周期内所做的功为0。当力与位移成90°相角，即与速度同相时，则在一个周期内所做的功为最大，等于力幅、振幅和圆周率的乘积。

我们再来考查作用在物体上的内力所做的功。由于弹性恢复力F_k=-kx=-kXsinωt与位移逆相，惯性力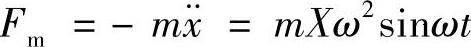与位移同相（见图1.18），因此，这两个力在一个周期里所做的功为0。进一步考查它们在每1/4周期里所做的功，可以发现：在第一及第三个1/4周期，弹性力做功-kX²/2，惯性力做功m（ωX）2/2；在第二及第四个1/4周期，弹性力做功kX²/2，惯性力做功-m（ωX）2/2。弹簧对物体（质量）做负功意味着物体对弹簧做正功，所做的功就是弹簧所具有的弹性势能；反之，则把弹性势能释放出来。惯性力并不是真正的作用力，而是由于物体具有加速度而表现出来的等效力，其所做的功与物体所具有的动能有关，做正功意味着动能被转化掉，做负功意味着转化为动能。所以，在第一及第三个1/4周期，动能转换为弹性势能；在第二及第四个1/4周期，弹性势能又转换为动能。在没有外力与阻尼的情况下，这个转化是等量的。因此，我们称弹簧和质量为储能元件。

而阻尼力由于与位移有90°相位差（与速度逆相），在一个周期里所做的功不为零，大小由式（1.13）给出，所做的功转化为热能而耗散掉。因此，把阻尼器称为耗能元件。