【摘要】:在每个瞬时,这些力的向量和等于0。图1.18 用旋转向量表示的各个力的关系随着旋转角速度ω的增加,阻尼力及惯性力的幅值随之增加,为了保持平衡,相位角ψ也要随之调整。事实上,根据图1.18在水平与垂直两个方向上列出的两个力的平衡方程,可以求得X、ψ,即幅频特性和相频特性,结果与式相同。
在激励力F(t)=F0 sinωt作用下,单自由度系统的稳态位移响应为
x=Xsin(ωt-ψ)
相应地,速度和加速度分别为
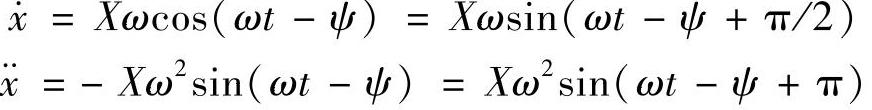
与位移相比,速度和加速度的相位分别超前了90°和180°。
另一方面,除了作用在物体上的激励力F(t)=F0 sinωt以外,还有以下内力
弹性力:Fk=-kx=-kXsin(ωt-ψ)(https://www.xing528.com)
阻尼力: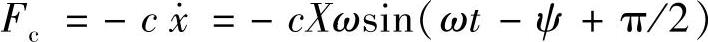
惯性力: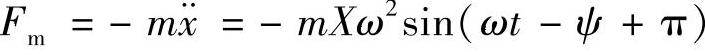
弹性力与位移反方向,阻尼力比弹性力超前90°,惯性力比弹性力超前180°,而激励力比位移超前相角ψ。如果用旋转向量来表示这些力之间的相位关系,则如图1.18所示。在每个瞬时,这些力的向量和等于0。
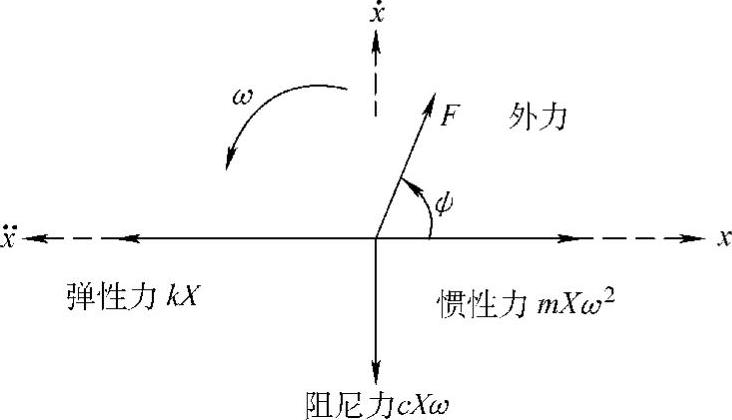
图1.18 用旋转向量表示的各个力的关系
随着旋转角速度ω的增加,阻尼力及惯性力的幅值随之增加,为了保持平衡,相位角ψ也要随之调整。例如当ω接近于0时,阻尼力及惯性力可忽略不计,为了平衡弹性力,ψ必须接近于0;而当ω非常大时,惯性力远远大于弹性力及阻尼力,ψ则必须接近于180°,以使激励力与惯性力相平衡;当ω=ωn时,弹性力与惯性力相互平衡(kX=mω2nX),ψ则必须等于90°,以使激励力与阻尼力相平衡,此时,激励力与速度同相。事实上,根据图1.18在水平与垂直两个方向上列出的两个力的平衡方程,可以求得X、ψ,即幅频特性和相频特性,结果与式(1.30′)相同。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




