强迫振动中的粘性阻尼效应

本小节考查有粘性阻尼的单自由度系统在外力作用下的强迫振动。外力的形式多种多样，可以是时间的任意函数。这里考虑角频率为ω的简谐外力F（t）=F₀sinωt。F₀为力幅，运动方程式为

这里我们只探讨欠阻尼的情况。式（1.28）所对应的齐次方程的通解已经由式（1.26）给出，只需要找到一个特解，即可求得该方程的通解。设该方程的特解为x=Asinωt+Bcosωt，代入上式并整理，通过对比左右两边三角函数的系数可求得

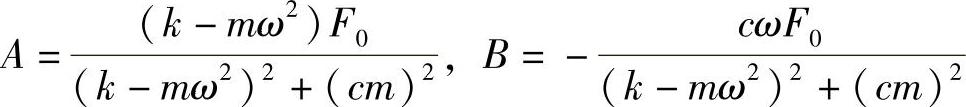
所以该方程的通解为

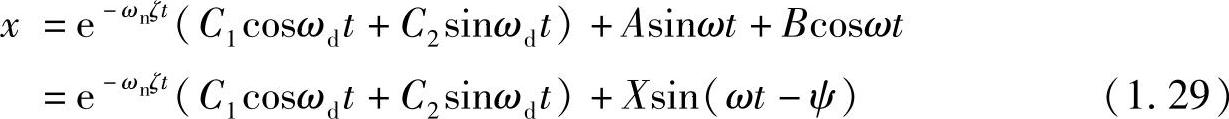
这里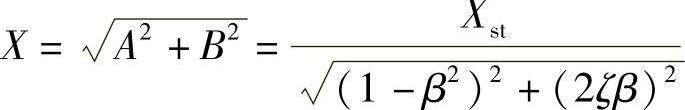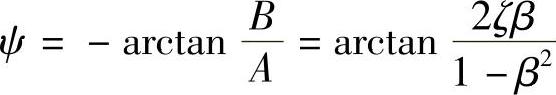，，。其中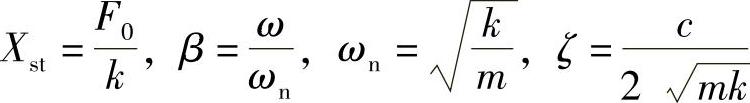，。C₁，C₂为两个由初始条件确定的常数。式（1.29）由两部分组成，第一项代表由初始条件引起的自由振动，第二项代表由外力引起的强迫振动。

图1.13 某薄板结构的阻尼处理前（虚线）后（实线）的冲击响应

这里考虑静止的初始条件，即x（0）=0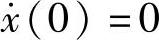，。对式（1.29）微分可得速度为

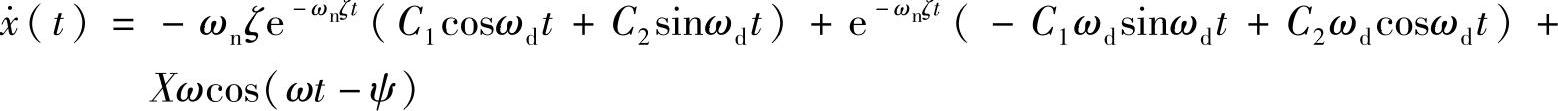
由初始条件x（0）=0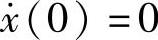，可得

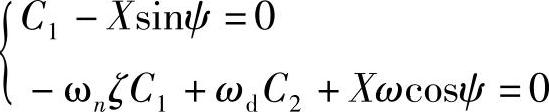
求解这个联立方程，可得两个待定常数C₁、C₂为

C₁=Xsinψ，C₂=X（ω_nζsinψ-ωcosψ）/ω_d有趣的是，静止的初始条件并没有得出C₁=0、C₂=0的结果。也就是说，式（1.29）第一项所代表的自由振动会发生。这点不同于上节所述的没有外力作用的自由振动的情况。如果没有外力作用，静止的初始条件当然不会引发振动。

可以这样理解，一个原来静止不动的物体，突然受到一个由正弦（余弦）函数定义的力的作用，在开始的瞬间，物体相当于受到了一个冲击作用，从而会引起在系统固有频率上的自由振动响应；随着时间的增加，在阻尼作用下，自由振动随之消失，只剩下做简谐振动的强迫振动。我们把激振开始产生的自由振动称为瞬态响应（Transient Response）。在这个非稳态的起振过程中，外力对物体做功，使其具有振动能量。经过一段时间后，瞬态响应消失，物体处于安定的简谐振动之中，即稳态响应（Steady State Response）。

也可以从信号分析的角度来理解。我们知道，只有在（-∞，∞）的时间上无限延续的正弦（余弦）信号才具有一个频率成分、有限长时间的正弦（余弦）函数，其时间信号里包含的频率成分并不是单频。方程式（1.28）中的激励力在t<0的时候假定为0。激振开始后（t>0）的短时间内，这个激励力信号里包含有丰富的频率成分，因而会引起在固有频率上的自由振动。只有当经过的时间足够长时，这个激励力信号才可以视为单频信号。

如图1.14所示为固有频率2Hz，阻尼比4%的单自由度系统在静止状态下用正弦激振的响应。调节激励力的大小，使得X_st=1。图1.14a为激励频率为0.5Hz的情况（ω/ω_n=0.25），在前两个周期里，还可以看到自由振动的影子，以后则只有强迫振动。图1.14b为激励频率为2Hz的情况（ω/ω_n=1），此时发生共振，振幅变得很大，但最终达到稳定状态（不像无阻尼情况那样越来越大，见图1.5）。图1.14c为激励频率为4Hz的情况（ω/ω_n=2），前5s可以清楚地看到自由振动衰减的情况。此后，只剩下振幅一定的强迫振动成分。

以上讨论的激励力是正弦函数的形式。容易证明，当激励力为余弦函数F（t）=F₀cosωt时，通解（1.29）依然成立，只不过相位角变为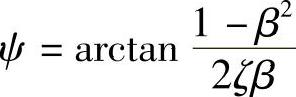。由于在t=0时刻，余弦激振相当于突然作用了一个大小为F₀的力，因而会引起更强的自由振动。

如图1.15所示为一个固有频率为3.2kHz、阻尼比为2%的单自由度系统在静止状态下（初始条件为0），分别用正弦激励力（F₀ sinωt）及余弦激励力（F₀ cosωt）激振时的位移响应（激振频率为500Hz）。相对于正弦激振，余弦激振的瞬态响应很显著。

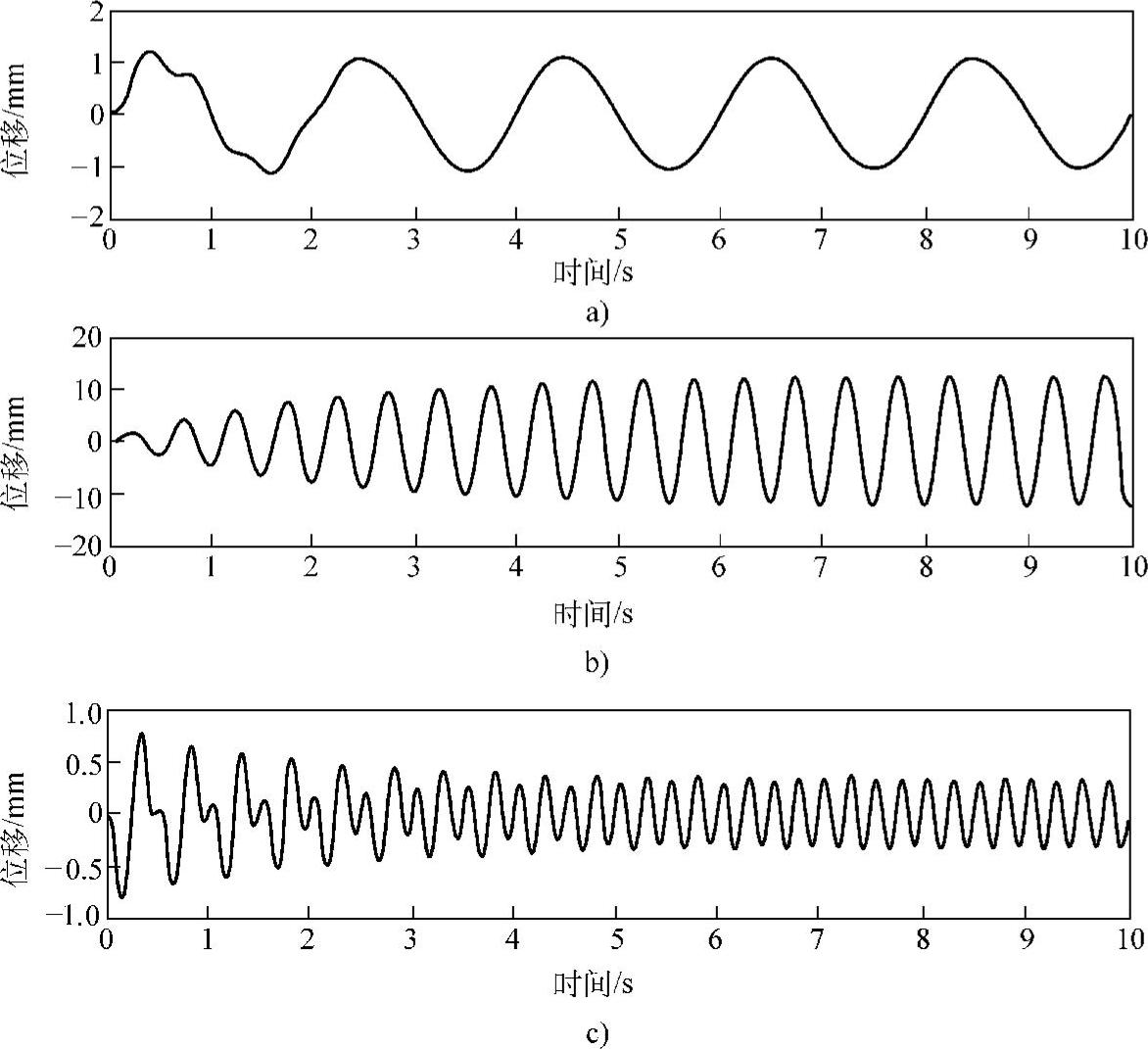
图1.14 单自由度系统（f_n=2Hz，ζ=0.04）的强迫振动响应

a）ω/ω_n=0.25 b）ω/ω_n=1 c）ω/ω_n=2

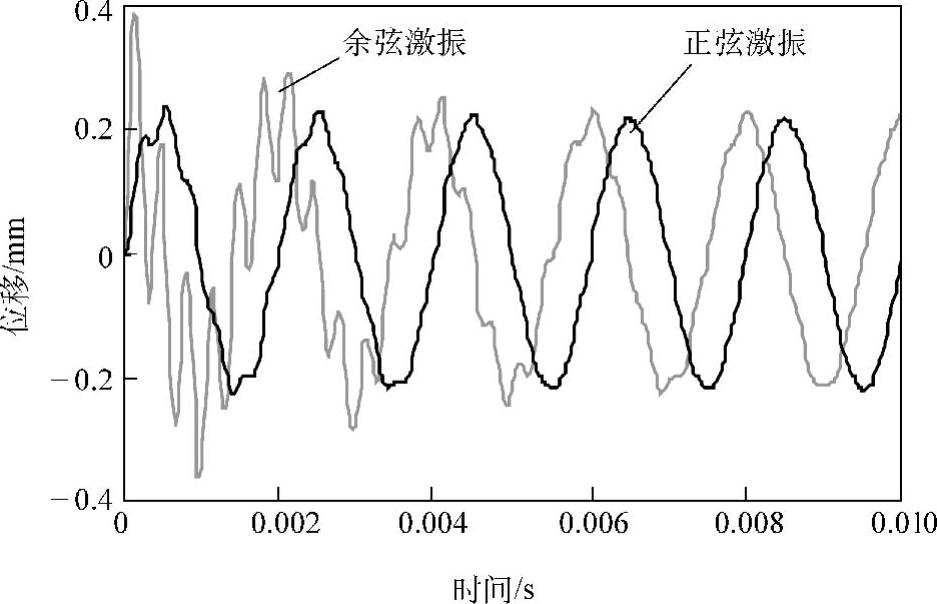
图1.15 单自由度系统（f_n=3.2kHz，ζ=0.02）的强迫振动响应（激振频率为500Hz）

由于瞬态响应会很快衰减掉，通常我们只需关心稳态振动的成分，式（1.29）可以写成

x=Xsin（ωt-ψ） （1.30）

其幅频特性和相频特性分别为

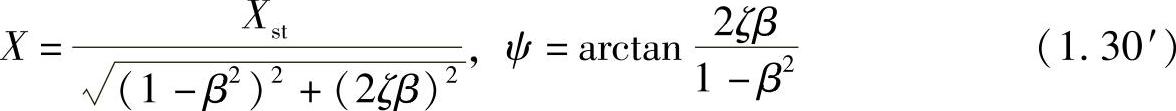
如图1.16所示为在不同阻尼比的情况下计算出的幅频特性（在此，正规化为X/X_st）和相频特性曲线。相频曲线的一个显著特点是，所有曲线在固有频率上相交于-90°位置，而与阻尼比无关。幅频特性的一个显著特点是，固有频率上的振幅随阻尼比变化很大，接近最大但并不为最大。

(www.xing528.com)

图1.16 不同阻尼比的强迫振动的相频特性和幅频特性曲线

a）相频特性曲线 b）幅频特性曲线

对比激励力F（t）=F₀sinωt和位移响应x=Xsin（ωt-ψ）可知，相位角ψ表示相对于激励力，位移响应所表现出来的相位滞后。当频率很小时（ω<<ω_n），二者相位差接近于0；当频率很大时（ω>>ω_n），二者相位差接近于180°；在固有频率处（ω=ω_n），二者相差90°。

对于幅频特性，当频率很小时（ω<<ω_n），X/X_st=1，振幅等于在同样大小静力作用下的静变形。此时，变形的大小仅取决于刚性。一般把这个领域称作刚性控制区。当频率很大时（ω>>ω_n），由于惯性的作用，物体跟不上激励力的变化而趋于静止不动，这个区域称为质量控制区。在固有频率附近（ω=ω_n），发生共振，振幅会变得很大。但是，由图1.16可见，增加阻尼可以有效地抑制振幅，这个区域称为阻尼控制区。

从振动控制的效果来讲，人们更关心振动的振幅。但是，在分析振动的机理时，相位特性也会提供重要的信息。例如只从振幅大小，有时可能无法判定是处于刚性控制区还是处于质量控制区，只有结合相位信息才能做出准确的判断。

我们已经知道，对于无阻尼系统，当激励频率等于固有频率时，振幅变为无穷大。但是，有阻尼系统只能产生有限大小的振幅。由于

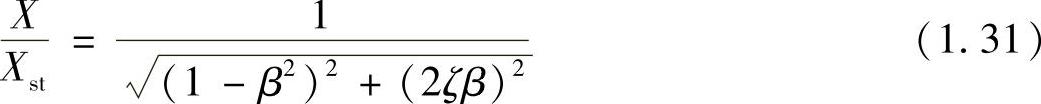
容易得到共振时（β=1）的振幅倍率为

可见，共振时的振幅倍率仅由阻尼比所决定。Q值为电气工程中的用语（Quality Factor），用于衡量共振时峰值的尖锐程度。

应注意的是，粘性阻尼系统的振幅的最大值并不发生在固有频率处。由式（1.31）可知，当该式分母最小时，振幅为最大。令g（β）=（1-β²）²+（2ζβ）²，则由∂g/∂β=0可以求出g为极小时的β取值。其结果为，即

注意：不要将式（1.33）与有阻尼固有频率的公式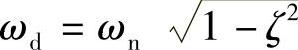相混淆。将式（1.33）代入式（1.31），可求得最大振幅倍率为

当阻尼比远小于1时，此式与式（1.32）等价。

严格地讲，当ω=ω_n时，发生共振的说法并不严密。从振幅最大的角度讲，共振实际上发生在式（1.33）所示频率上，这个频率称为共振频率。

在1.2.2节中，我们介绍了柔顺性函数的概念。这里，我们用前面所介绍的振动的复指数表示方法来推导有阻尼单自由度系统的柔顺性函数。

引入复指数表示方法，单频激励力可以写为F（t）=F₀e^jωt。于是，运动方程为

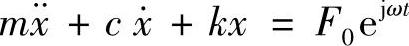
设上式的解为x=Xe^jωt，代入后可得

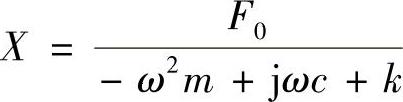
因此，柔顺性函数为

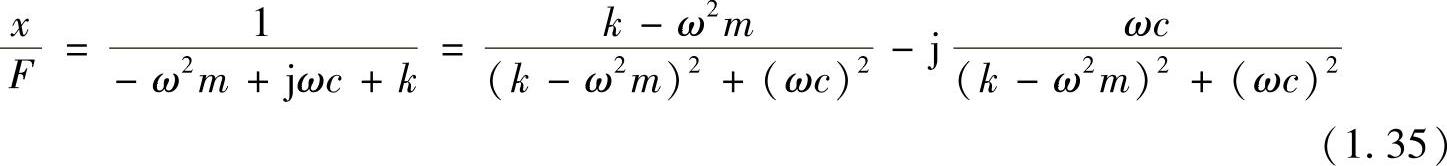
进一步可求得幅频特性和相频特性为

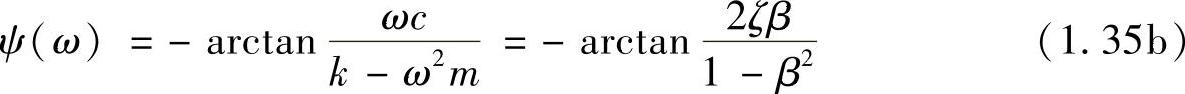
这里，引入与式（1.29）同样的参数定义：

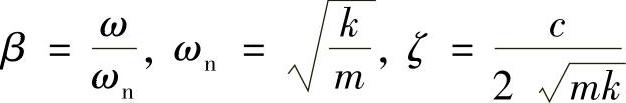
式（1.35a）与式（1.31）等价，唯一的不同是纵轴的量纲不同。因此，图1.16也代表了柔顺性函数的特性。另外，从以上推导过程可以看出，运用振动的复指数表示方法进行演算很方便。