流体阻尼中的结构阻尼及其作用机理

在实际中，如果没有持续的外界能量的供给，任何振动都会经过一段时间后停下来。我们把这种使振动逐渐衰减下来的作用称为阻尼（Damping）。阻尼是物质或结构的一种物理性质，其产生机理多种多样。例如流体一般都具有粘性，当物体在粘性流体中振动时，就会受到由此粘性而产生的阻力作用，称为粘性阻尼（Viscous Damping）。尽管阻尼的表现形式为阻止振动的阻力作用（即阻尼力），应注意阻尼和阻力不是同一量，就像质量和重力不是同一物理量一样。流体阻尼除了粘性引起的以外，还有由于湍流引起的阻尼作用。粘性阻尼力与振动速度成正比，而湍流阻尼力与速度的平方成正比。

固体表面的干摩擦即库仑摩擦（Coulomb’s Friction），所产生的阻尼力与速度无关，仅取决于表面的摩擦因数及正压力的大小，称为摩擦阻尼。

而当固体发生变形时，由于材料内部的摩擦及蠕变等作用也会引起阻尼作用，称为材料阻尼。我们知道，摩擦作用会使两个物体在切线方向上胶着在一起（Stick-ing），只有使它们分离的剪切力足够大时，两个物体才产生相对滑动（Slipping）。一旦滑动，即使取消剪切力，它们也不会恢复到原来的位置。依此类推，当固体发生变形时，由于内摩擦的作用，一般来说，剪切应力-应变迟滞曲线（见图1.8a）为一个封闭曲线。另外，固体分子的排列不整，存在空穴。空穴的移动（蠕变）需要消耗能量，同时使得位移滞后于动态作用力，形成应力-应变迟滞曲线，如图1.8b所示。一个振动周期内固体阻尼所消耗的能量就等于这个曲线所围成的面积。因此，固体材料阻尼又称为迟滞阻尼（Hysteretic Damping）。

一方面，金属材料的内阻尼（材料阻尼）一般很小，所以，工业应用中经常需要使用粘弹性材料等阻尼材料来进行减振降噪处理；另一方面，实际的机械产品都是由许多零部件装配而成，由于结合面的摩擦、接触等因素的影响，整体结构所表现出来的阻尼要比材料内阻尼大几个量级。我们把整体结构所表现出来的阻尼称作结构阻尼（Structural Damping）。通常说法中，结构阻尼也包含上述固体材料阻尼或迟滞阻尼。

图1.8 切应力-应变迟滞曲线的概念图

a）内摩擦模型 b）内摩擦+蠕变模型

还有一些其他形式的阻尼，例如磁性阻尼、磁粘性流体（MR fluid）阻尼等，在此不予深究。对于机械工程师来说，理解好粘性阻尼及结构阻尼的特性，对于掌握振动力学的基础尤为重要。

粘性阻尼力与速度成正比，设阻尼系数为c（单位：N·s/m），则阻尼力大小为

对于简谐振动，x（t）=x_a sin（ωt），阻尼力在一个周期内所消耗的能量为

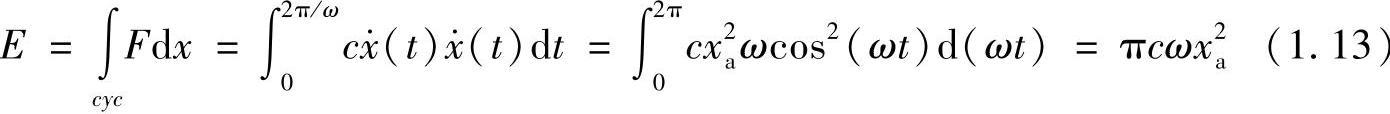(www.xing528.com)

即粘性阻尼消耗的能量与振幅的平方成正比，同时还与振动频率成正比。

对于结构阻尼或迟滞阻尼，不像粘性阻尼那样在数学上容易处理。大量实验表明，简谐振动一个周期内，迟滞阻尼所消耗的能量与振动频率无关，而只与振幅平方成正比，即

E_h=αx²_a （1.14）

这里，α是一个常数。对比式（1.13）和（1.14），可以从能量等价的角度得到等效的粘性阻尼系数为

因此，阻尼力可以写为

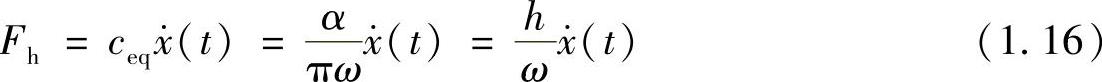
其中，h称为迟滞阻尼常数或结构阻尼常数，单位与刚性系数一样，为N/m。上式表示一个简单的结构阻尼的模型，即结构阻尼力与速度成正比，同时与振动频率成反比。

对于简谐振动，根据式（1.6），式（1.16）可以进一步写成

F_h=jhx（t） （1.17）

也就是说，可以把结构阻尼系数看作为一个用虚数表示的刚性。当然，这只是为了在数学上处理方便起见，它并不像真正的刚性那样具有实际物理含义。