无阻尼单自由度系统的自由振动：振动响应与极坐标表示形式

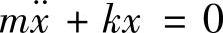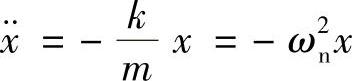单自由度无阻尼系统的振动由微分方程式（1.1）所决定。略去时间变量t，该方程可以写为或，其中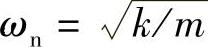，。这个方程有两个显而易见的特解：x=sinω_nt，x=cosω_nt。所以，该方程的通解为

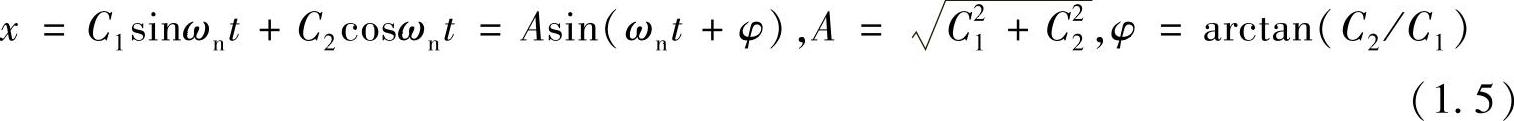
A称为振幅，φ称为相位，二者由初始条件所决定。假设初始时（t=0）位移为x₀，速度为v₀，将该条件代入位移方程式（1.5）及其微分（速度）可以求得

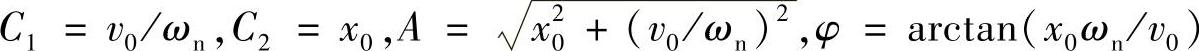
例如把图1.1的物体拉开x₀然后释放（初始速度为0），则有A=x₀，φ=π/2。此时，物体的位移为

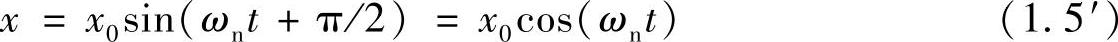
可见，无阻尼单自由度系统的振动响应可以用一个正弦（或余弦）函数来表示，其振动周期为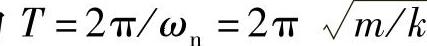。由于这个周期仅取决于系统的质量与弹簧刚性，称之为固有周期（Natural Period），其倒数称为固有频率f_n（Natural Frequency，单位为Hz）。相应地，ω_n称为固有角频率（Natural Angular Frequency，[rad/s]）。这种振动称为简谐振动或单频振动（Simple Harmonic Vibration）。

对于简谐振动来说，用一个正弦或余弦函数足以描述其响应。但是在研究复杂的振动形式时，三角函数并不是最好用的数学表达方式。这里，我们介绍用复数形式表示振动的方法。应用欧拉公式e±jθ=cosθ±jsinθ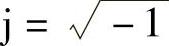，，上式可以变形为

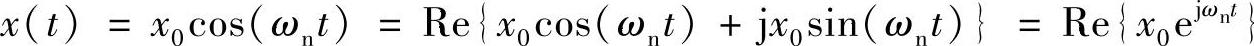
Re表示取实部。可见，简谐振动可以用一个复指数的实部来表示，复指数可以用复平面上的一个向量来表示。图1.3表示一个长度为A的向量在复平面上的逆时针方向以ω_n的角速度旋转时的情况。很显然，它在实轴上的投影就是一个简谐振动x（t）=Acos（ω_nt）。(www.xing528.com)

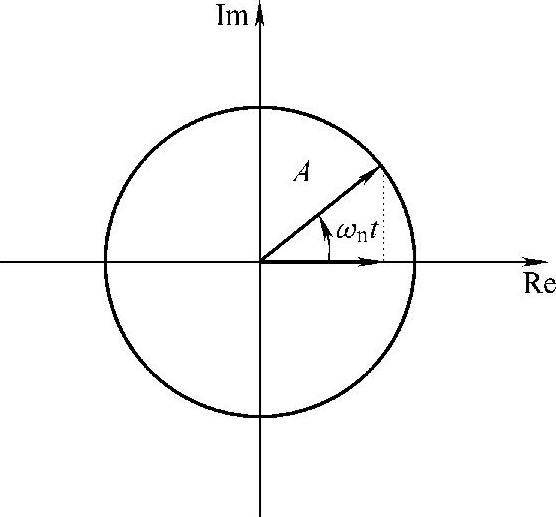
图1.3 简谐振动的向量表示形式

为了方便，通常略去实部，而直接用复指数形式来表示一个单频振动，这种形式也称为极坐标表示形式。这在数学演绎推导过程中毫无问题，只要对最终结果取实部即可。简谐振动的位移、速度和加速度用极坐标形式表示，有以下关系

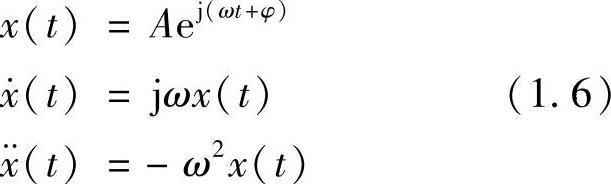
如图1.4 所示为初始位移为1mm，初始速度为0，固有频率为2Hz的单自由度系统的自由振动的位移、速度和加速度曲线。速度与位移呈现90°的相位差，而加速度与位移相位刚好相反。这里，速度由位移的1阶微分得到，加速度由位移的2阶微分得到。另外，为了便于与位移及速度同图表示，加速度的单位取为Gal（1Gal=1cm/s²）。结合式（1.6）可知，给一个向量乘上虚数单位j相当于把这个向量前移90°相角，而幅值保持不变。

最后，对频率及角频率的关系做一说明。图1.3中，向量转过一圈所用的时间定义为周期。频率定义为周期的倒数，表示每秒钟内转过的圈数，单位为1/s。所谓角频率，其实是向量旋转的角速度，即每秒转过的角度，单位为rad/s。因此，角频率与频率的关系为ω_n=2π f_n。

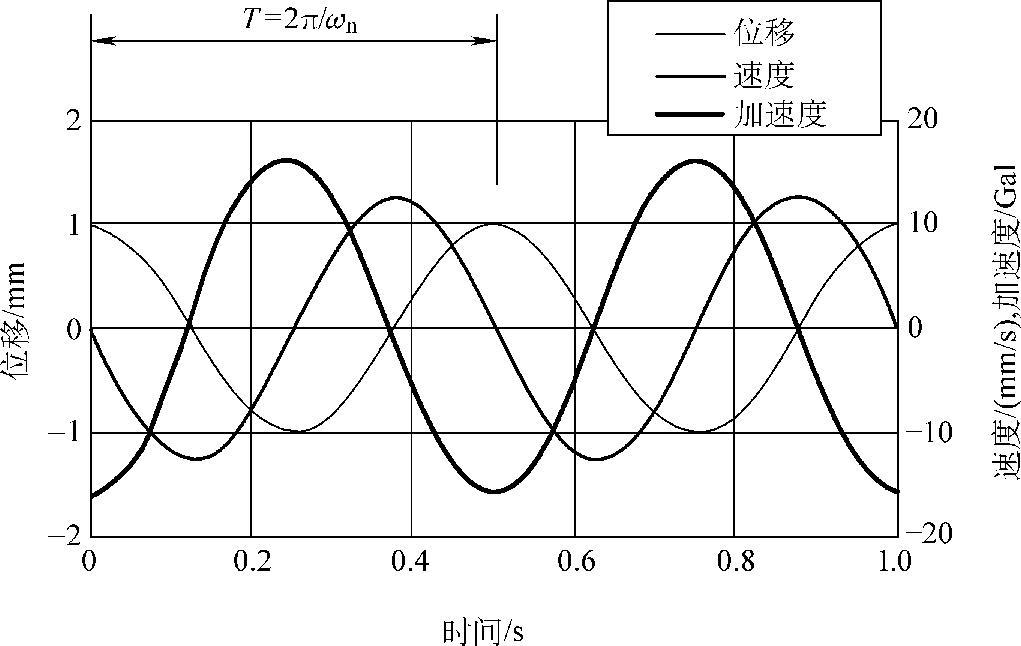
图1.4 无阻尼单自由度系统的自由振动