学习机械振动的最基本力学模型——单自由度系统

自由度（Degree Of Freedom，DOF）是指描述一个物体的运动所需要的独立变量的个数。我们知道，一个在空间没有约束的刚体，它可以沿坐标轴X、Y、Z三个方向平移，也可以绕这3个轴旋转。我们称这个物体具有6个自由度，也就是说，用3个平移变量和3个旋转变量就可完全描述一个刚体的运动。

实际的机械结构都是连续的弹性体结构，理论上具有无限多的自由度。例如在桌面上敲击一下，桌面的各个部分将会产生垂直于桌面的振动（称为横向振动）。尽管振动会很快地衰减下去，要完全地描述这个振动现象，需要桌面上所有位置的位移情报，即无限多个变量。理论上这是无法完成的任务，但所幸的是，完整的桌面振动情报对我们并无多大用处，我们所关心的可能只是桌面在敲击下所产生的振动及噪声的频率成分及其衰减特性，这是用数点甚至一点的情报即可实现的。这种用有限个变量来描述具有无限个自由度的连续体振动的方法称为低阶自由度模型化方法。

考虑一种最简单的情况，一个质点被限制在一个方向上运动，这个系统称为单自由度系统（Single Degree Of Freedom，SDOF）。这时，用一个变量即可完全描述质点的运动。单自由度系统是学习机械振动的最基本力学模型，实际中的很多复杂系统在一定条件下都可以简化成单自由度系统来处理。因此，掌握好单自由度系统的动态特性非常重要。

图1.1表示一个理想化的单自由度系统。质量为m的物体系在不计质量、弹性系数为k的弹簧一端，弹簧的另一端固定。物体与支持面之间不存在摩擦，而且物体只能沿着弹簧轴线方向（这里称为X方向）运动。

图1.1 单自由度振动系统的力学模型

把物体从其初始平衡位置拉开，然后释放，物体在弹簧恢复力的作用下将做返回其初始位置的运动。在到达其初始位置时，物体获得最大动能而不会停下来，在惯性的作用下将继续前行，弹簧则被压缩。在压缩到与被拉伸同等距离的时候，动能完全转化为弹性势能，物体瞬时速度变为0。此后，弹簧恢复力又开始作用，物体再次向反方向运动。如此周而复始，物体做以初始位置为原点的往复运动，即振动。

考查图1.1中的物体运动，不难发现：作用在物体上的力只有一个弹簧恢复力，它遵循胡克定律，力的大小等于弹性系数与位移的乘积，而作用方向与位移相反。于是，根据牛顿运动定律可得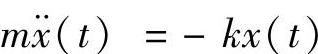：，因此，物体运动可以用以下齐次型微分方程来表示

这是在没有外力作用情况下（这里的弹簧力为内力）的振动，称为自由振动。上式也可以理解为，在每个时刻，弹簧恢复力与惯性力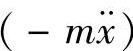处于平衡状态。

如果有外力F（t）作用在物体上迫使其振动，则称为强迫振动。这时物体受到的力为弹簧恢复力与外力之和，-kx（t）+F（t），运动方程变为以下非齐次型微分方程(www.xing528.com)

可见，机械振动是一个求解常微分方程的问题。在这个系统中，质量和弹簧是两个不可或缺的元件。由方程式（1.2）可知，若m=0，则变成一个受力变形问题；若k=0，则变成一个单纯的运动问题。因此，一谈到机械振动，就应该联想到一个质量弹簧系统。这里，弹簧并不限于常见的卷簧（Coil Spring），而是指一切具有抵抗变形能力的刚性元件（stiffness）。

如图1.1所示模型代表了直线振动的情况。弹性支撑下的汽车发动机的上下振动就可用该模型表示。还有一种振动形式是绕着某个轴在回转方向做往复运动，如图1.2所示。将一个圆盘（齿轮或者飞轮）安装在一端固定的主轴上，把圆盘转过一个小角度θ（单位：rad），然后释放，圆盘将产生扭转振动。设圆盘的惯性矩为J（单位：N·m²），轴的扭转刚性为k_t（单位：N·m/rad），则系统的运动方程为

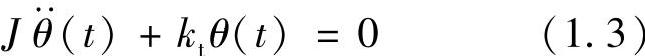
如果有外转矩T（t）（单位：N·m）作用在圆盘上，则运动方程为

可见，扭转振动的方程式与直线振动的方程式形式完全相同，当然，解法也相同。

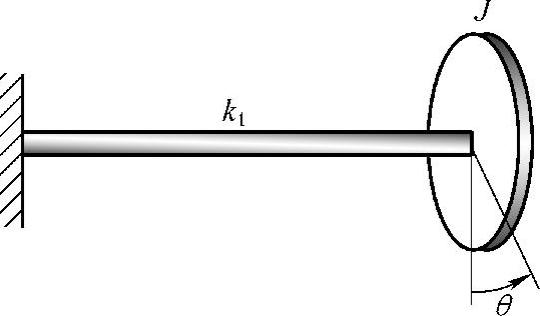
图1.2 扭转振动系统