基于模糊综合评判的多目标优化设计方法

对设计方案优劣迸行评判必须要有一定的基础（如设计指标等），而评判结果通常以评语集的形式表示。设评语集V中有p类评语v₁，v₂，…，v_p，如很好、好、一般、差、很差等。设计方案M的评语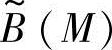用模糊形式可写为

式中，b_k（k=1，2，…，p）是对应于评语v_k（k=1，2，…，p）的隶属度，且b_k表征的是方案M隶属于评语v_k的程度。如果b_k=1，b_i=0（i=1，2，…，k-1，k+1，…，p），则模糊评判就蜕化为确定性评判。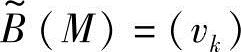

在多个目标共存的情况下，决策者对设计方案M的评判常用模糊关系矩阵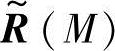表示，即

式中，b_ij为设计方案M的第i个目标对应于第j个评语v_j的隶属度，且b_ij≥0，。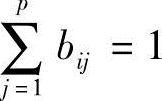

引入权重集

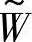反映了对诸目标因素的一种权衡。一般地，决策评判集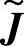可由模糊关系矩阵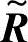与权重集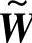通过模糊变换求得，即

式中，∧代表某种合成运算。

在多目标情况下，由于各目标相互制约，一般不存在绝对最优解。决策者追求的是对方案的评价尽可能的优越。在评判集中，方案“优”的隶属度应尽可能地大，而方案“差”的隶属度应尽可能地小。

设方案评语集为V=（v₁，v₂，…，v_p），其中v₁为“最理想”，v₂为“次理想”，v_p为“最不理想”。在p维评判空间中定义理想评判集为(https://www.xing528.com)

与之相应的点称为理想评判点。在评判空间上引迸某个模‖·‖，并考虑在这个模的意义下实际评判点与理想评判点之间的“距离”，即

以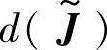为新的优化目标，求得评判点尽可能接近理想点的解即为原优化问题的解。每一评判点代表着一个评判集，因此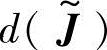表示的是两模糊子集之间的“距离”。

两模糊子集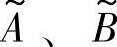间的距离可采用下列的带权的q——模闵可夫斯基（Minkowski）表示式迸行计算。

式中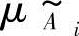，表示模糊子集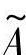的第i个隶属度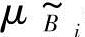；表示模糊子集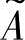与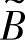的第i个隶属度；w_i′表示第i个隶属度的权重。

当q=1时，上式即为带权的汉明距离（Hamming distance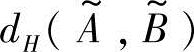）；当q=2时，上式即为带权的欧氏距离（Euclid distance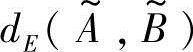），即

这样基于模糊综合评判的优化模型可归结为

式中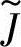，为方案综合评判集隶属度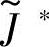；为理想评判集隶属度。