普通多目标模糊优化问题的求解

这类多目标模糊优化问题的数学模型为

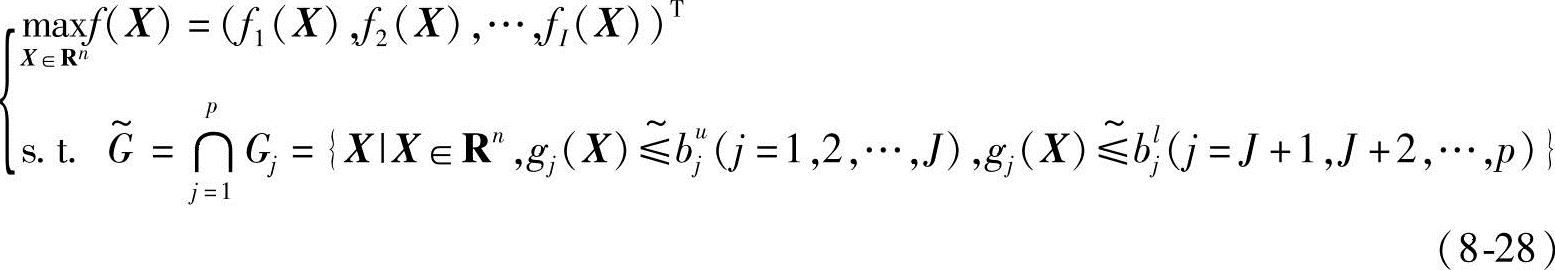
对于中每一模糊约束的约束上下限给出容差d_j，并采用线性隶属函数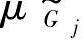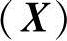，如图8-7所示，则

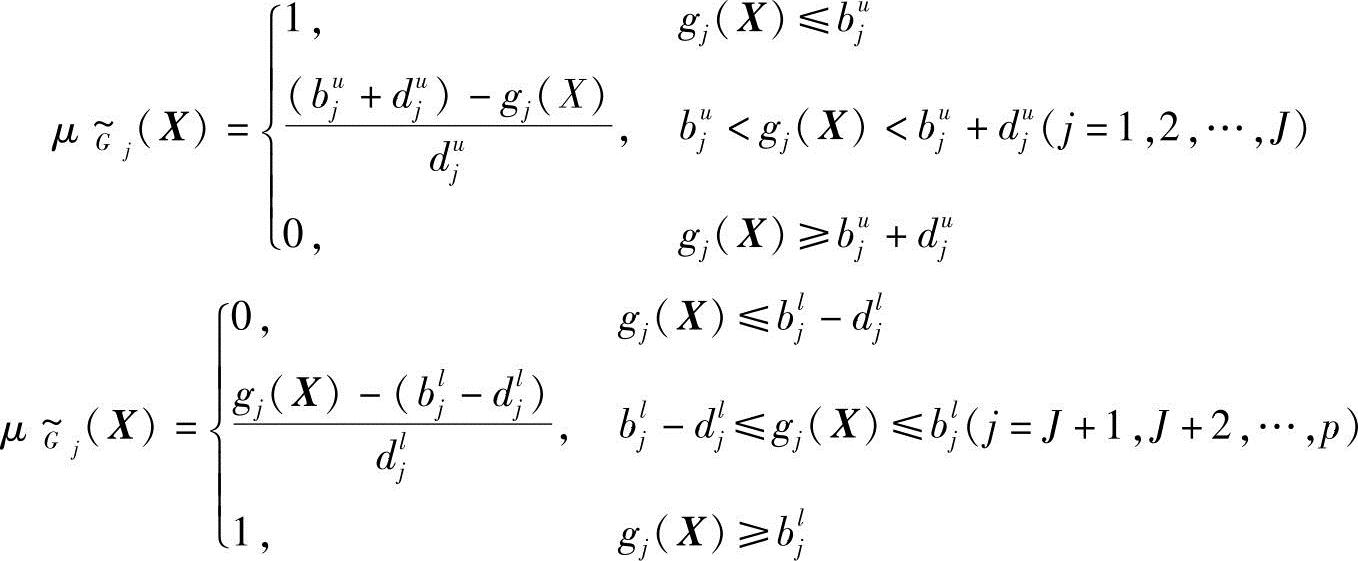
图8-7 线性隶属函数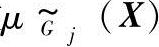

应该指出，各子目标函数f_i（X）（i=1，2，…，I）可能的最小值m_i受到约束条件模糊性的影响，而其可能的最大值M_i又受到其子目标函数最小点的影响。因此，在满足模糊约束条件的多目标优化情况下，各子目标函数f_i（X）将在特定的区间内变化，形成模糊目标最小集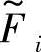。构造隶属函数的具体步骤如下

1）求各子目标函数在约束条件最宽松情况下可能的最小值，即

用常规优化方法求得其解为X_i*，最小值为f_i（X_i^*）。将X_i^*代入其余的子目标函数，得f_l（X_i^*）（l=1，2，…，I，l≠i）。

2）找出各子目标函数可能的最小值m_i和最大值M_i，即

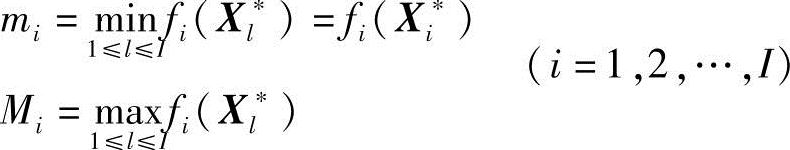
3）构造各子目标函数模糊目标集的隶属函数

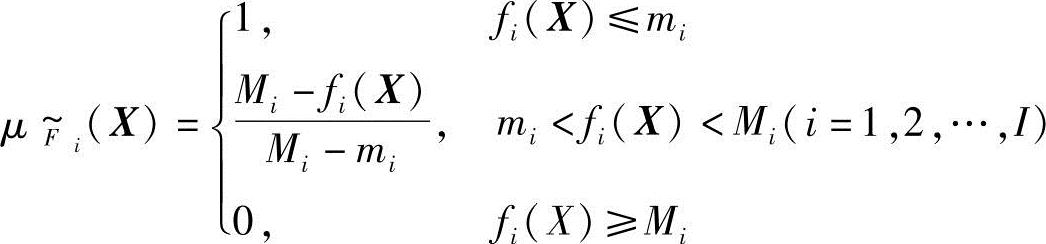
4）构造综合模糊目标集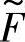和综合模糊约束集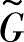的模糊判决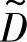的隶属函数，求出最优点X^*使最优判决为

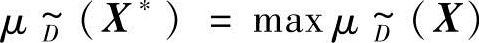
为适应对工程设计不同决策思想的需要，可采用不同形式的模糊判决：交模糊判决、凸模糊判决和积模糊判决。(https://www.xing528.com)

交模糊判决的隶属函数定义为

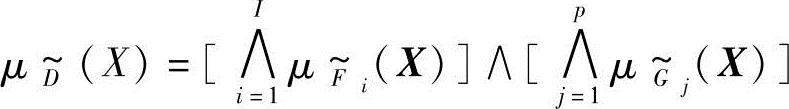
则式（8-28）所示的普通多目标模糊优化问题转化为

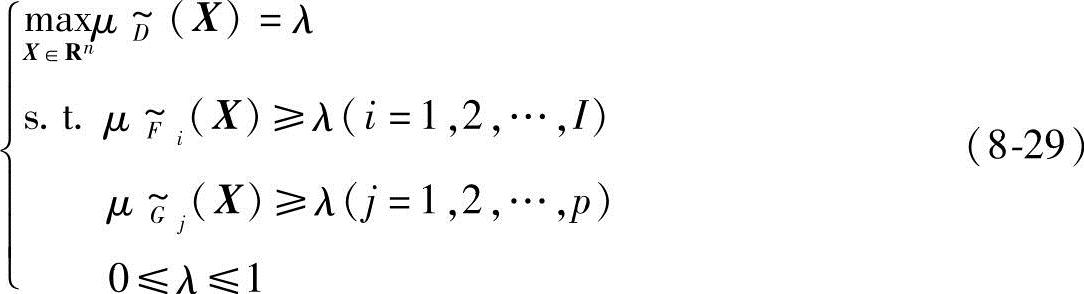
凸模糊判决的隶属函数定义为

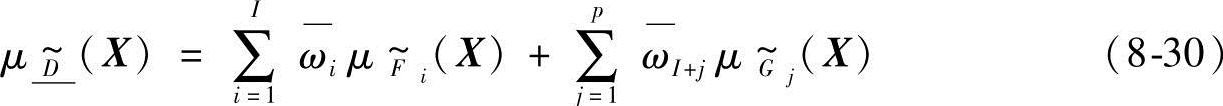
其中

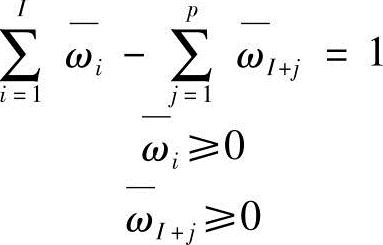
则式（8-28）所示的普通多目标模糊优化问题转化为

积模糊判决的隶属函数定义为

则式（8-28）所示的普通多目标模糊优化问题转化为

经过严格的理论证明，应用上述不同形式的模糊判决求得的满意解均为弱有效解。交模糊判决反映了使各子目标和各约束中最差分量得到改善的谨慎思想，其结果仅使最差分量极大化，而其余量在一定范围内变化并不直接影响结果，丢失了不少信息。凸模糊判决属于算术平均型判决，它涉及各子目标、各约束之间的相对重要性，反映了对各方面均有所考虑的平均思想，表达明确、直观，巨对重要指标的作用易于掌握。积模糊判决属于几何平均型判决，即从几何平均意义上考虑各子目标、各约束分量的影响。