最优水平截集法：提高数据处理效率再升级

1.求解原理

如果只有约束条件是模糊的，而目标函数是清晰的，则该模糊优化问题为非对称模糊优化问题，可利用最优水平截集法求解。

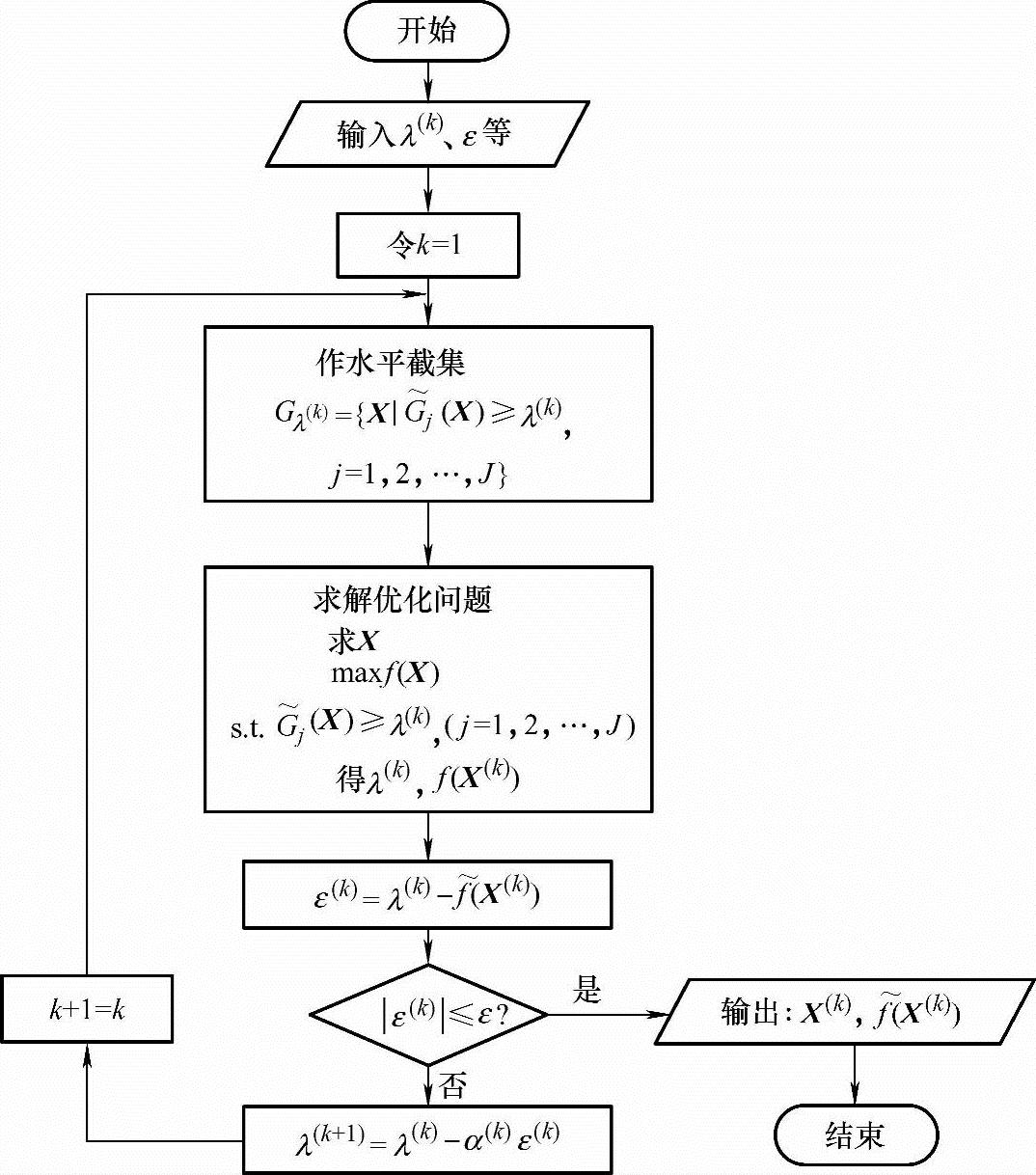
图8-5 对称模糊优化解的迭代框图

设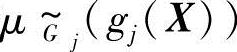为物理量g_j（X）对模糊允许区间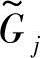的隶属度，则g_j（X）对模糊约束的满足度，可记为

当β_j=1时，该约束得到严格的满足；当β_j=0时，该约束未得到满足；当0＜β_j＜1时，该约束得到一定程度的满足。

模糊允许范围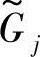在设计空间划出一个具有模糊边界的模糊允许域和模糊不允许域，因此，所有模糊约束在设计空间围成了一个具有模糊边界的可用域，记为

式（8-22）表示设计空间的模糊可用域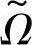是所有模糊约束空间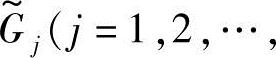的交集。也就是说，中的每一个可用点是所有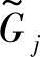的可用点，它们在满足度大于零的意义下满足所有模糊约束。

对于广义模糊约束来说，可将模糊约束记为

式（8-23）表示广义模糊约束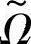就是要求模糊约束函数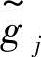在模糊意义下落入模糊允许区间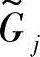。因此，对此模糊约束的满足度β_j必须根据模糊约束函数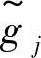的隶属函数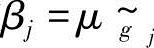的图形，以及它的模糊允许区间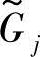的隶属函数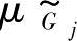的图形的相对位置来定义。

如图8-6所示，当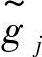完全落入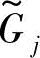内时，相当于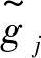的隶属函数图形完全落入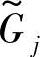的隶属函数图形内，约束得到完全满足，此时满足度β_j=1；当μ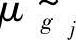和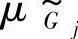的图形重叠时，约束得到一定程度的满足，此时0＜β_j＜1；

当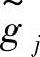的隶属函数图形落入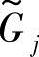的隶属函数图外时，约束完全没有得到满足，此时满足度β_j=0。

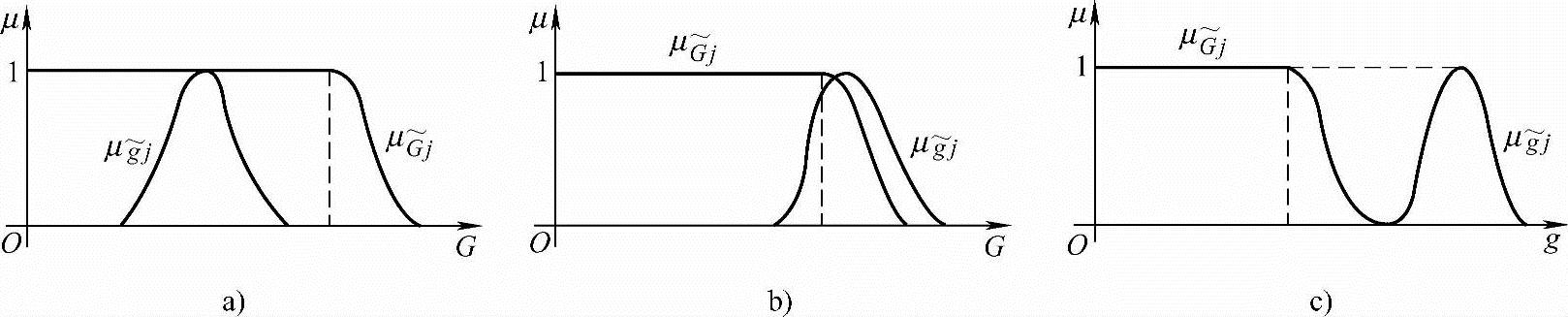
图8-6 模糊约束满足度

a）β_j=1 b）0＜β_j＜1 c）β_j=0

2.普通模糊约束的优化问题

根据上述原理，其求解的基本思想是：通过λ水平截集将模糊子集分解为若干个普通集合G_λ，然后求目标函数f（X）在G_λ上的极值，迸而求得在上的模糊条件极值，即在模糊允许区间中，在隶属度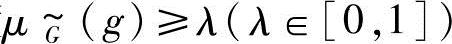的区间构成实数论域上的一个普通子集，即

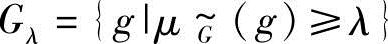
可以看出，两个不同的水平截集满足

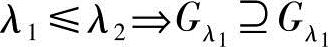
即λ值越小，G_λ的区间就越大，当λ=0时，包括了全部的允许域；当λ=1时，变为最严格的区间。因此在机械结构模糊优化设计过程中，λ可以理解为“设计水平”的概念，在实际优化过程中可以取不同的值，便得到一系列的水平最优解，供决策者选择，其中必然存在一个最优的λ^*，与之相应的水平截集为

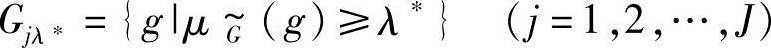
G_jλ^*称为最优水平截集。用此水平截集代替全部的模糊允许区间，模糊优化问题可以转化为具有设计水平的非模糊优化问题，即(www.xing528.com)

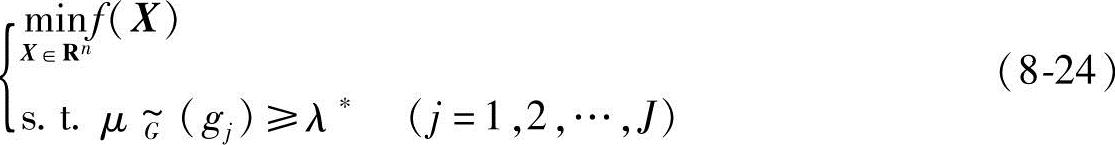
因此，具有普通模糊约束的非对称模糊优化问题的具体解题步骤如下：

1）使约束条件模糊化，建立各个模糊允许区间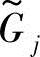的隶属函数；

2）寻求一最优水平值λ^*；

3）作模糊约束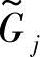的最优水平截集G_jλ^*，将模糊问题转化为G_jλ^*上的常规优化问题；

4）用常规的解法求式（8-24），即得到模糊优化问题的最优解X^*。

3.广义模糊约束的优化问题

广义模糊约束的优化问题求解方法与普通模糊优化问题的基本一致，即引入一λ，将广义模糊约束的优化问题转化为求常规优化问题，即

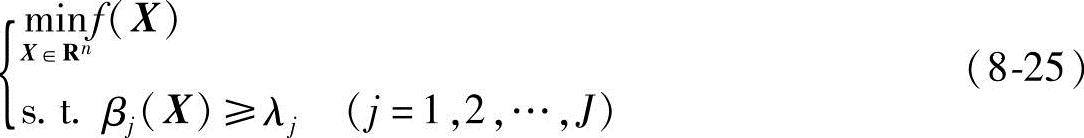
改变λ值可得到一系列普通优化模型，从而得到一系列优化方案，如果已求得最优水平λ^*，则可得到相应的最优水平截集，即

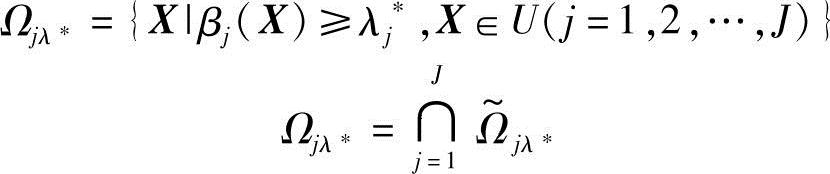
则模糊优化问题可记为

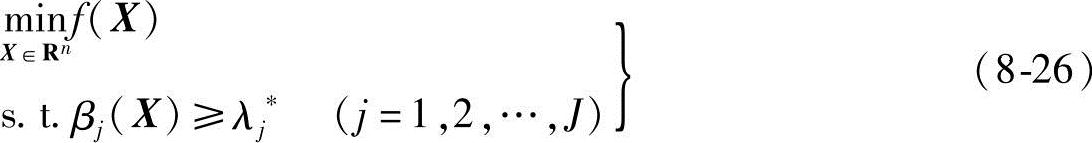
综上所述，求解具有广义模糊约束的非对称模糊优化问题的最优水平截集法步骤如下：

1）建立设计变量X对广义模糊约束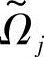的满足度β_j（X）；

2）寻求一最优水平值λ^*；

3）作模糊约束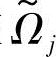的最优水平截集Ω_jλ^*，将模糊问题转化为Ω_jλ^*上的常规优化问题；

4）用常规的解法求式（8-26），即得到模糊优化问题的最优解X^*。

4.最优水平截集的确定

用最优水平截集法求解模糊优化问题时，关键问题是确定最优水平截集，即确定最优的值，主要有规划法和模糊综合评判法。

1）规划法的基本思想是：由于最优λ^*值应使得结构既安全可靠，又经济节省，因此λ^*值应根据结构的初始造价G（X_λ）和结构使用中所需补充的费用（维修费用、灾害损失费用等）的期望值E（X_λ）来决定。初始造价和期望值既是X_λ的函数，故也是λ的函数。随着λ的增大，G（X_λ）值增大，E（X_λ）值减小，因此，确定λ^*的问题，可归结为求解如下的数学规划问题，即

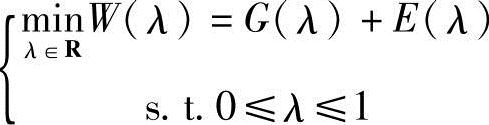
此规划问题的最优解，即为所求的最优λ^*值。

2）模糊综合评判法就是应用模糊变换原理对其所考虑的事物迸行综合评价。当对上述的最优水平值迸行决策时，凡是对结构安全可靠和经济节省有影响的因素，如设计水平、制造水平、材料好坏、重要程度、使用条件、维修保养费等，都可以作为集中因素加以考虑。首先建立因素集、评价集，迸行单因素模糊评判，建立权重集，最后迸行模糊综合评判，根据需要可采用一级模糊综合评判、二级模糊综合评判和多级模糊综合评判，详细步骤见有关的参考资料。