数学模型：优化模糊优化

迸行模糊优化设计之前，首先要建立其数学模型，与普通优化设计的数学模型一样，模糊优化的数学模型也包括设计变量、目标函数和约束条件三个基本要素。

1.设计变量

设计变量为设计过程中所选的非相关的变化量，一般包括结构的几何参数、材料特性参数等。由于设计问题的复杂性，设计变量可以是确定的、随机的和模糊的。

2.目标函数

目标函数是衡量设计优劣的指标，根据问题的性质，可以有一个或多个目标函数。目标函数一般包括结构的质量、造价、刚度、固有频率、惯量和可靠性等性能指标。设计方案的优劣本身就是一个模糊概念，没有确定的界限和标准，特别是对于多目标优化设计，目标函数之间通常都是相互矛盾的，往往得不到理想解，而只能得到满意解。如果目标函数是模糊的，记作。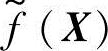

3.约束条件(www.xing528.com)

约束条件在设计空间中形成一个可行域，只有满足所有约束条件的设计才认为是可行设计，否则为不可行设计。约束条件一般分为三个方面：一是几何约束，如结构尺寸与形状约束等；二是性能约束、如应力约束、刚度约束、位移约束、频率约束和稳定性约束等；三是人文因素约束，如政治形式约束、经济政策约束、环境因素约束等。以上约束条件，特别是人文因素约束和性能约束条件中，包含大量的模糊信息。根据约束的模糊性质，又把模糊约束分为两类。

（2）普通模糊约束 当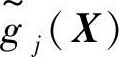为非模糊量时，约束条件变为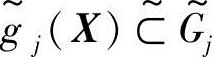，这是工程设计中最常见的一种情况，其意义为确定量g_j^（X）在模糊意义下落入模糊允许区间。

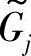设计变量、目标函数和约束条件，三者都可以是模糊的，也可以某一方面是模糊的而其他方面是确定的或随机的，但只要其中一项包含了模糊信息，该优化问题即为模糊优化问题。当设计变量、目标函数和约束条件中都具有模糊性时，模糊优化的数学模型可以表示为