隶属函数的选择及其影响

隶属函数的选取在模糊优化问题的求解中是极其重要的，函数形状将直接影响最终的模糊最优解。判别隶属函数是否符合实际，不是看单个元素的隶属度的数值如何，而是要看这个函数是否正确反映了元素从属于集合到不属于集合这一变化过程的整体特性。模糊数学已总结出隶属函数的多种方法，可在实际应用中参考。

1.常用的两种隶属函数形式

（1）正态型这是最常见的一种分布，有以下3种。

1）降半正态型

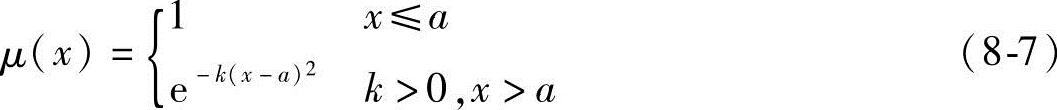
2）升半正态型

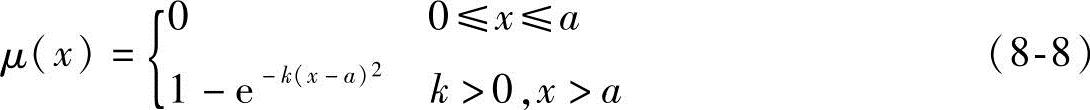
3）正态对称型

上述正态对称型适用于模糊变量具有某种对称性质，巨随着偏离某中心位置，模糊变量的隶属程度将不断减小，如某零件“磨损量大约为某值”这一模糊事物，就可选用这种隶属函数加以描述。正态非对称型可用来描述模糊变量上下界取值的模糊允许范围。

（2）梯形分布

1）降半梯形分布(www.xing528.com)

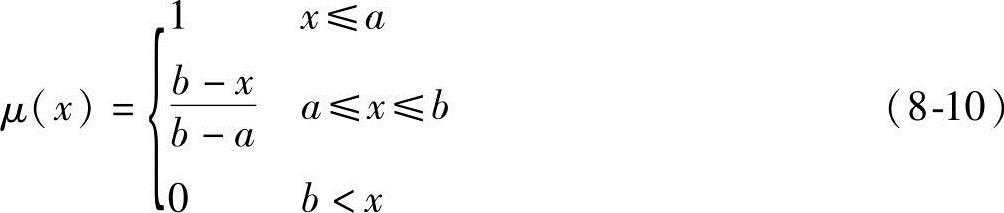
2）升半梯形分布

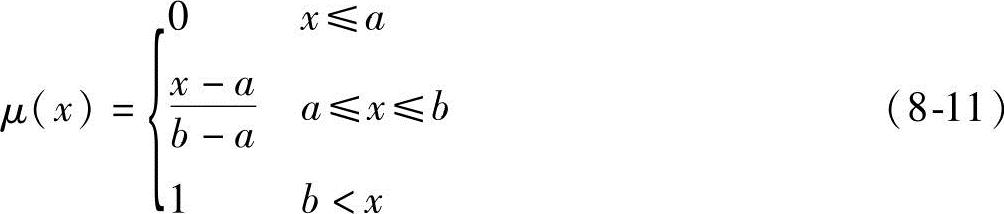
3）对称梯形分布小

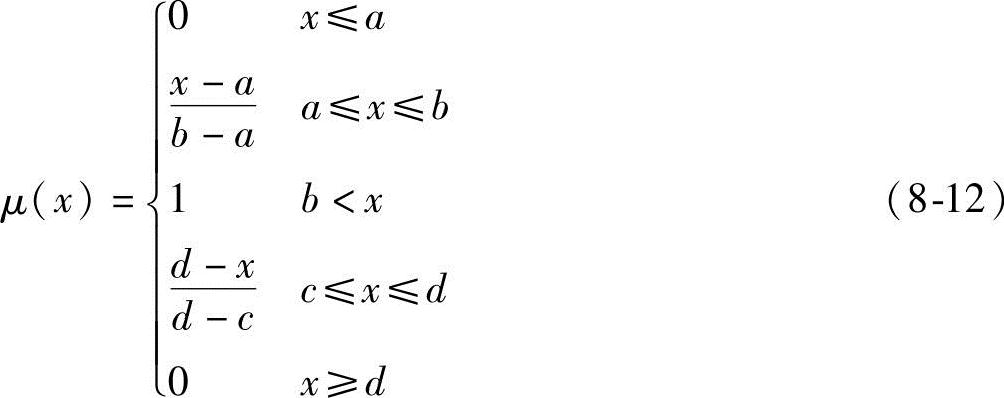
上述分布适用于模糊现象呈简单线性变化的情况。工程设计中为简化起见，通常将模糊设计变量上下界的取值区间用梯形分布隶属函数加以描述。

2.其他常用隶属函数类型及突出重要程度参数调整方式

在多目标模糊优化中，目标之间经常是相互矛盾的，根据各目标的重要程度，选取合适的隶属函数数值，可调整最优解在设计空间的位置，使之向重要目标靠近，增加重要目标最优解的影响。其他常用隶属函数类型及参数调整方式见表8-1。

表8-1 常用隶属函数类型及参数调整方式

一般来说，从重要到不重要的目标，选取隶属函数的优先顺序依次为：尖Γ型、锥型、柯西型和抛物线型。上述顺序不是绝对的，隶属函数的形状一方面决定于其类型，另一方面还取决于其参数的大小。