1.模糊集的定义
给定论域U上的一个模糊集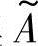 是指:对任何u∈U,都指定了一个数
是指:对任何u∈U,都指定了一个数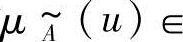 [0,1]与之对应,它叫作u对
[0,1]与之对应,它叫作u对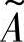 的隶属度,这意味着做出了一个映射,即
的隶属度,这意味着做出了一个映射,即
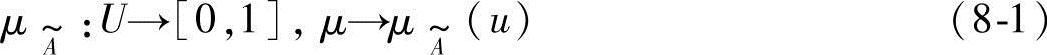
这个映射称为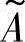 的隶属函数,其中的波浪号表示变量或运算中含有模糊信息,如图8-1所示。
的隶属函数,其中的波浪号表示变量或运算中含有模糊信息,如图8-1所示。
模糊集完全由隶属函数刻画。特别地,当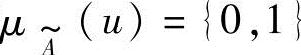 时,
时,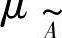 便蜕化为一个普通集合的特征函数,于是
便蜕化为一个普通集合的特征函数,于是 便蜕化为一个普通集合
便蜕化为一个普通集合
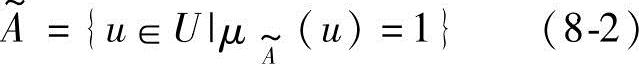
因此,普通集合是模糊集的特殊情况,而模糊集是普通集合的扩展。
2.模糊集的表示方法
模糊集的表示方法一般有三种,设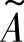 为论域U上的模糊集合,
为论域U上的模糊集合, 中的元素为{a,b,c,d,e},各元素所对应的隶属函数为{1,0.8,0.4,0.2,0}。
中的元素为{a,b,c,d,e},各元素所对应的隶属函数为{1,0.8,0.4,0.2,0}。
(1)查德表示法
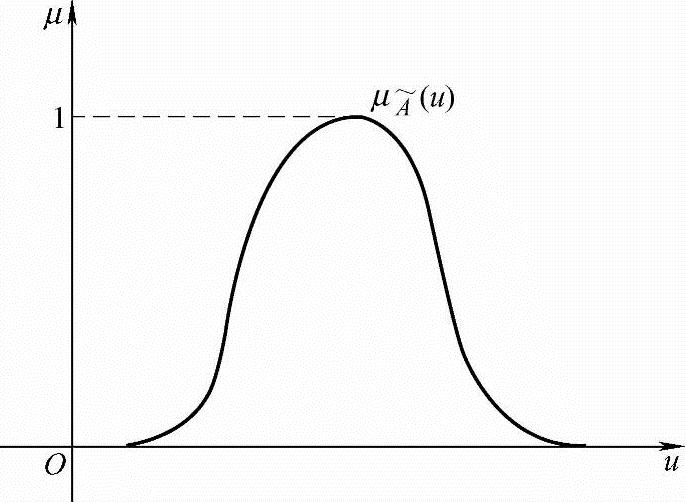
图8-1 模糊集合的隶属函数
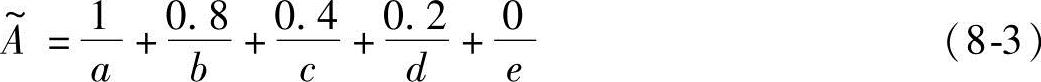
这里右端项并非分式求和,它仅仅是一种记号,分母位置为论域U的元素,分子位置为相应元素的隶属度。
当U是连续论域时,给出如下记法:
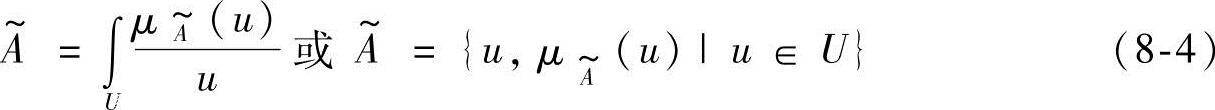
式中的积分号不是通常积分的意思,而是表示各个元素与其隶属度对应关系的一个总括。(https://www.xing528.com)
(2)序偶表示法
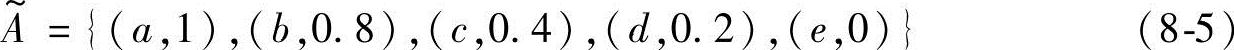
其中每一元素是个序偶(x,y),第一个分量x表示论域中的元素,第二个分量y表示相应元素的隶属度。
(3)向量表示法

3.模糊集的基木运算
设 为论域U上的两个模糊集合,则规定模糊集之间的包含
为论域U上的两个模糊集合,则规定模糊集之间的包含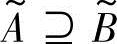 、相等
、相等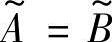 、并
、并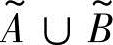 、交
、交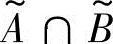 、余
、余 ,运算如下:
,运算如下:
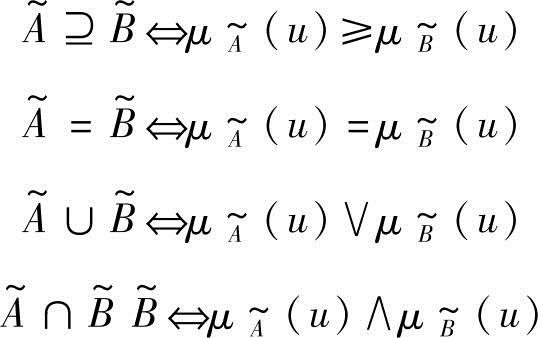
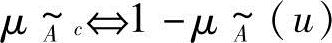
模糊集的并、交、余运算的几何意义如图8-2所示。
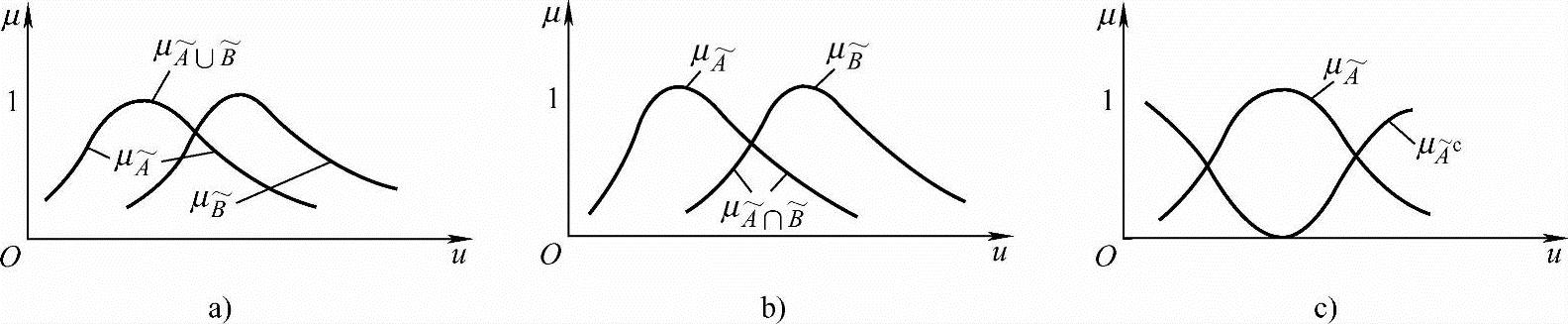
图8-2 模糊集的基本运算
a)模糊集的并运算 b)模糊集的交运算 c)模糊集的余运算
这些运算具有幂等律、交换律、结合律、吸收律、分配律、两极律、复原律和对偶律等性质。并和交的运算还有多种其他定义,但常用的是取大和取小运算,这是由于它们计算简单,而巨能为模糊决策分析提供合理的解释。
除了以上的并、交、余基本运算之外,模糊集还有许多其他运算,如模糊集的差、代数和、代数积、有界和、有界积、爱因斯坦积与和以及Hamacher积与和等。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




