优化设计实例：离散变量的最佳实践

例题 如图7-11所示，设有一箱形盖板，已知长度l₀=600cm，宽度b=60cm，厚度t_s=0.5cm。翼板厚度为t_fcm，它承受最大的单位载荷q=0.01MPa，要求在满足强度、刚度和稳定性等条件下，设计一个重量最轻的结构方案。

解：（1）设计分析

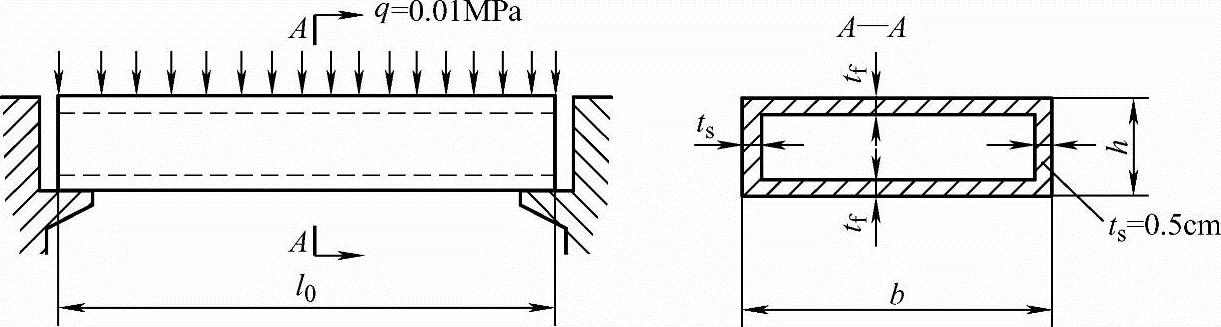
图7-11 箱形盖板尺寸图

设箱形盖板为铝合金制成，其弹性模量E=7×10⁴MPa，泊松比μ=0.3，允许弯曲应力［σ_b]=70MPa，允许切应力τ=45MPa。经过力学分析，得出如下公式及数据。

截面的惯性矩近似取

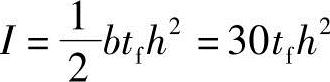
最大切应力为

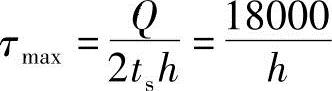
最大弯曲应力（翼板中间）为

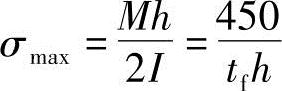
式中，Q为最大剪力，Q=18000N。

翼板中的屈曲临界稳定应力为

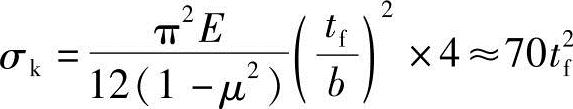
最大挠度为

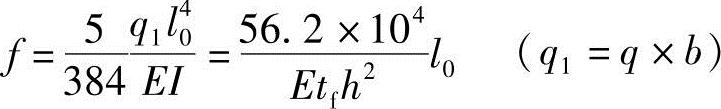
盖板单位长度的质量（kg/cm）为

W=ρ（120t_f+h）

式中，ρ为材料的密度，单位为t/cm³。

（2）数学模型

根据设计要求，建立如下数学模型：

设计变量为

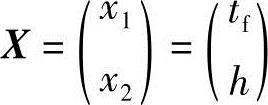
目标函数为

f（X）=120x₁+x₂

式中已略去密度ρ，因为它对目标函数极小化没有影响。

设计约束：按照强度、刚度和稳定性要求建立如下约束条件：

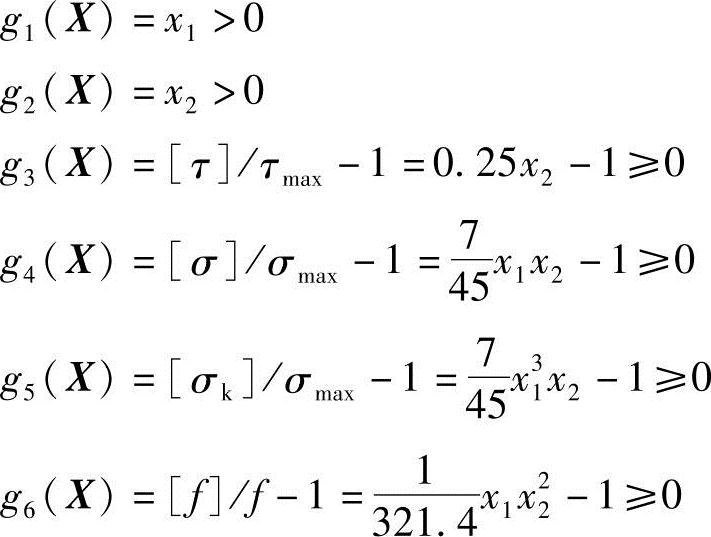(www.xing528.com)

单位长度允许挠度取［f]/l₀=1/400。

在图7-12中给出了这个问题在设计平面上的几何关系：f（X）的等值线和约束边界曲线g₁（X）～g₆（X）。阴影线的右边为可行设计区域，其最优解在P点。

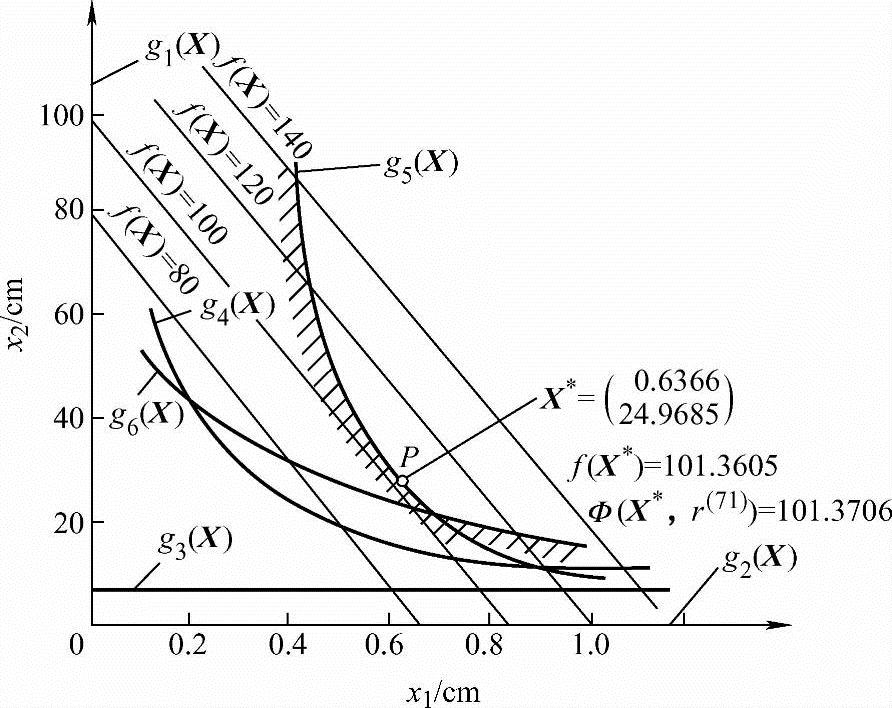
图7-12 箱形盖板优化设计空间关系

（3）求解方法和结果

用内点惩罚函数法来解这个问题。其惩罚函数如下式：

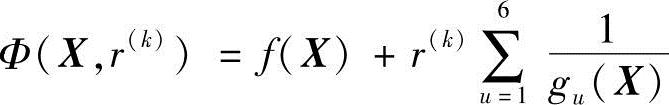
初始点取X^（0）=（1，30）^T，是一个可行点。取惩罚函数因子初始值r^（0）=3，缩减系数c=0.7，收敛精度ε=10^-6，用鲍威尔方法求函数Φ（X，r^（k））的无约束优化极值，其计算结果见表7-1。

表7-1 用内点惩罚函数法求解盖板问题（x₁=t_f，x₂=h单位：cm）

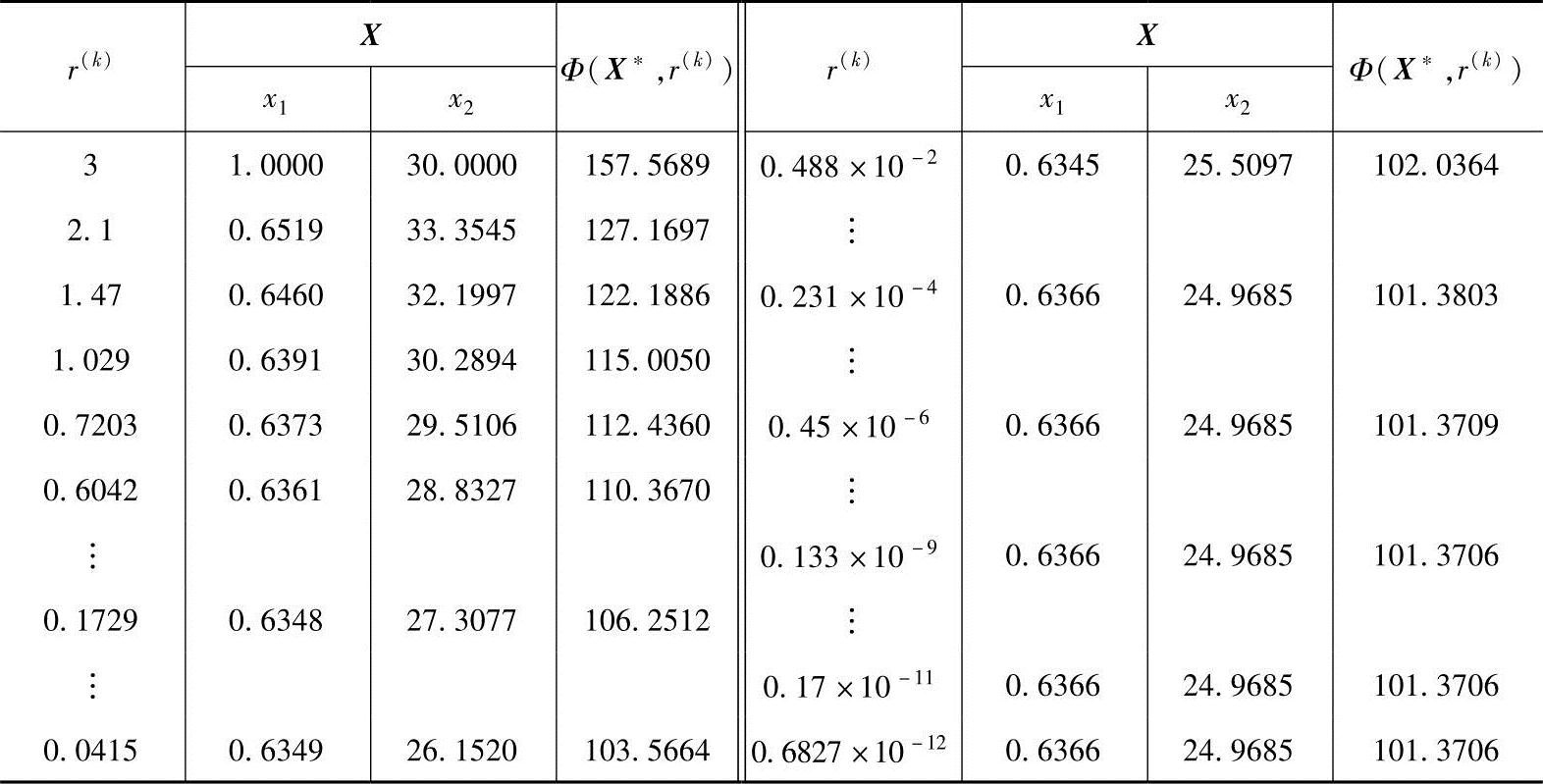
共循环k=71次，r值由3降至0.6827×10^-12，迭代129次，其最优解为x₁^*=0.6366，x₂^*=24.9685，f（X^*）=101.3605，Φ（X^*，r^（71））=101.3706，由于r值几乎趋近于零，所以说明取得了较精确的解答。

在图7-13中给出了三个r值分别为2.1，1.47和0.488×10^-2的惩罚函数Φ（X^*，r^（k））等值线的图形，表明了条件极小点逐渐向真正最优点靠拢。

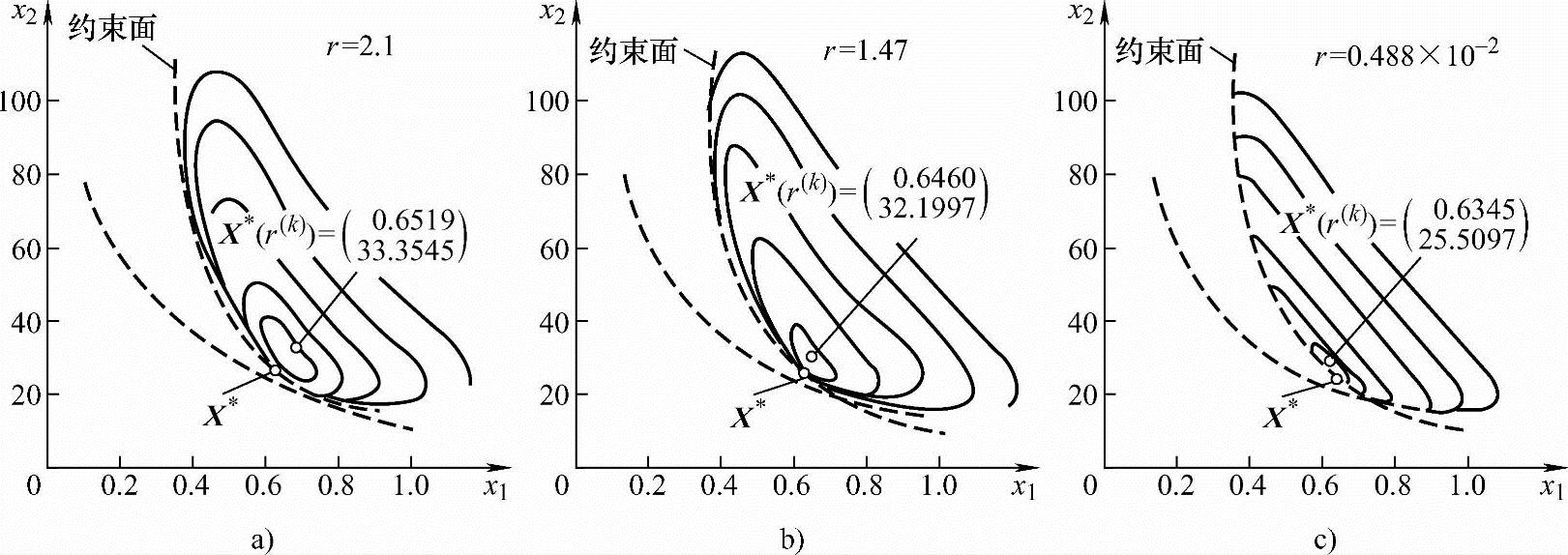
图7-13 用内点惩罚函数法求解箱形盖板问题的空间关系

接下来用离散变量法优化此问题。若取设计变量的离散值为

x^D₁=t_f=0.0cm，0.1cm，0.2cm，0.3cm，…

x₂^D=h=15.0cm，25.0cm，40.0cm，60.0cm，…

该问题为全离散问题，其数学模型为

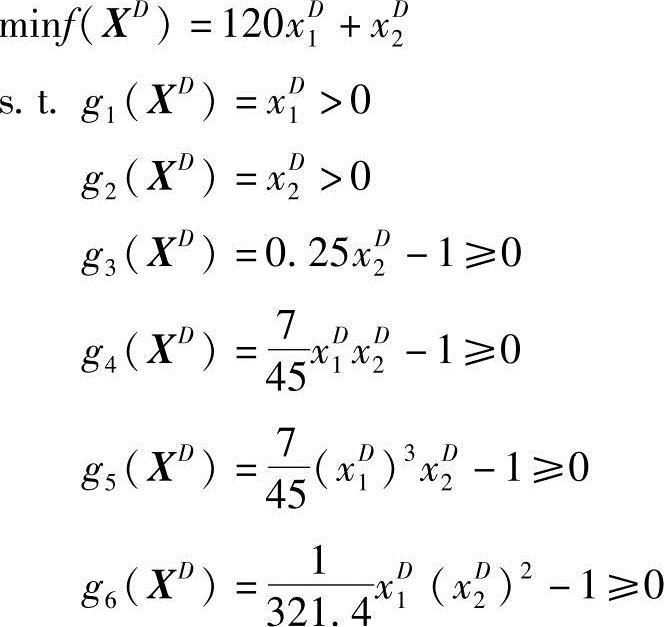
求X^D=（x^D₁，x^D₂）^T

下面分别用离散随机搜索法、离散变量组合形法和离散惩罚函数法迸行计算，并取得相同的离散最优解：x^D₁=0.7，x^D₂=25.0，表7-2列出了计算的有关数据，图7-14表示了按离散变量设计的设计空间关系。

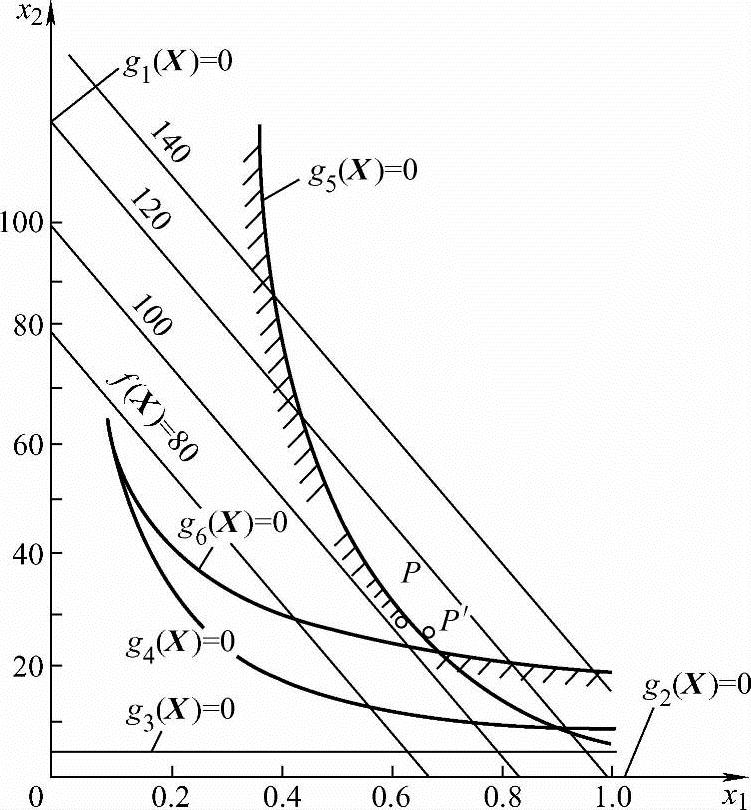
图7-14 按离散变量设计箱形盖板的设计空间关系

表7-2 三种离散优化方法的计算结果

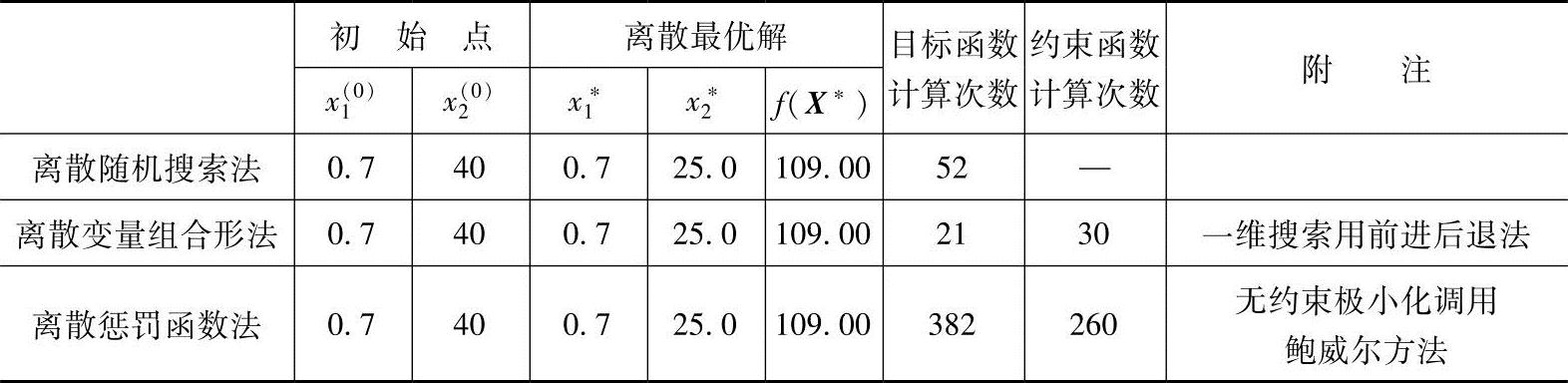
由表7-2可以看出，虽然三种方法都能取得相同的计算结果，但其计算效率却显著不同。最后还应该说明，目前现有的离散优化方法还不能说是十分完善的，因为它们的解题能力与计算效率都与数学模型的性态有很大关系。因此，迸一步研究通用性强、可靠和高效的约束非线性离散变量优化设计方法，不仅具有重要的理论价值，而巨也具有非常重要的工程实际意义。