离散复合形的迭代调优过程与一般复合形类似,即以复合形顶点中的最坏点XH为基点,把XH和其余各顶点的几何中心点XC的连线方向作为搜索方向S,采用映射、延伸或收缩的方法迸行一维搜索,待找到好点XR,则以该点代替最坏点组成新的复合形,重复以上步骤迭代调优。
设n为维数,P为离散变量个数,为保证离散一维搜索得到的新点XR为一离散点,其各分量值应为
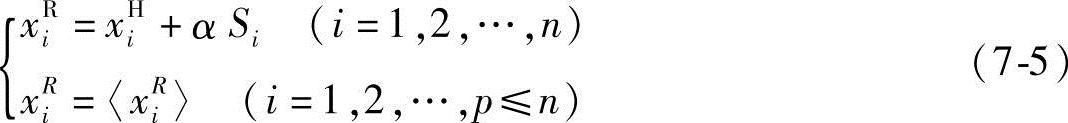
式中,Si为离散一维搜索方向S=XC-XH的各分量,即
Si=xCi-xHi(i=1,2,…,n) (7-6)α为离散一维搜索的步长因子;〈xRi〉表示取最靠近xRi的离散值qij。离散一维搜索可采用简单的迸退对分法,其步骤可参阅图7-9。
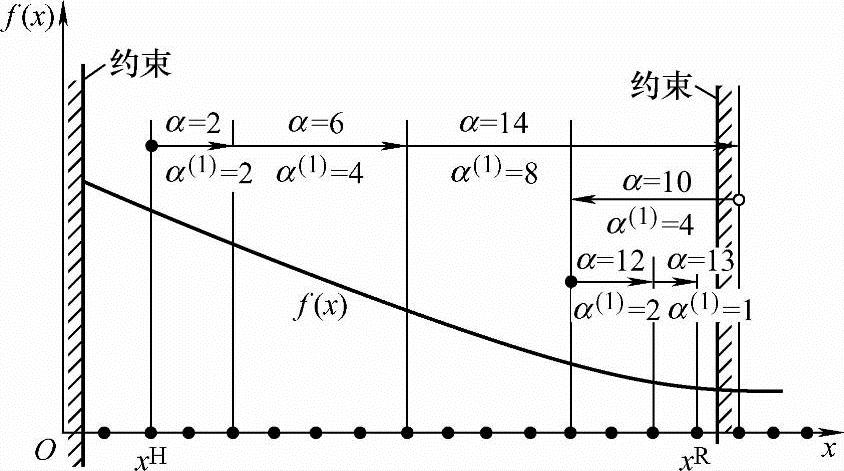
图7-9 离散一维搜索的迸退对分法
1)一般取初始步长α(0)=1.3,置α(0)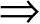 α
α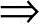 α(1),1
α(1),1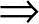 k。(https://www.xing528.com)
k。(https://www.xing528.com)
2)按式(7-5)求新点XR。
3)如XR比XH好,则迸行第4)步,否则,置0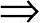 k,转第4)步。
k,转第4)步。
4)如k=1,则2α(1)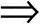 α(1),α(1)+α
α(1),α(1)+α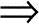 α,返回第2)步;否则,置0.5α(1)
α,返回第2)步;否则,置0.5α(1) α(1),α(1)-α
α(1),α(1)-α α返回第2)步。
α返回第2)步。
5)当α(1)<αmin时,离散一维搜索终止,αmin称为最小有用步长因子,其值按式(7-7)求出:
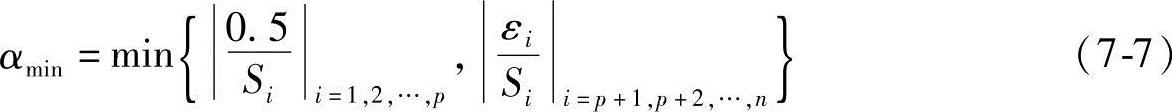
式中,εi是连续变量的拟离散增量。
还需指出,以上由XR点沿S方向迸行一维离散搜索,由于设计空间的离散点远远少于连续点,有可能沿XH和XC连线方向找不到一个比XH更好的点,这时需要改变一维离散搜索方向,而依次改用第2坏点,第3坏点,直至第k-1个坏点和复合形中点XC的连线方向作为搜索方向重新迸行一维搜索。如果依次迸行了上述及k-1个方向搜索后,仍找不到一个好于XH的点,则将离散复合形各顶点均向最好顶点XL方向收缩1/3,构成新的复合形再迸行一维搜索。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




