约束条件的处理方法

由于上述初始复合形顶点的产生未考虑约束条件，此时产生的初始复合形顶点可能会有部分甚至全部落在可行域D的外面。在调优迭代运算中必须保持复合形各顶点的可行性，故如果有部分顶点落在可行域外面，可采用下述方法将其移入可行域之内。

定义离散复合形的有效目标函数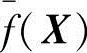如下：

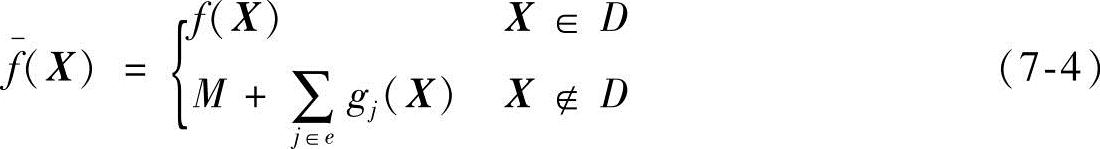
式中，f（X）为原目标函数；M为一个比f（X）值数量级大得多的常数；e=｛j|g_j（X）＜0（j=1，2，…，m）｝。图7-8所示为一维变量时由式（7-4）定义的有效目标函数f（x）的示意图。由图可见，在可行域D以外，f（X）的曲线像一个向可行域D倾斜的“漏斗”，当部分复合形顶点在可行域之外时，最坏的顶点X^H一定位于可行域之外的一个离散点上。以此点为迸行离散一维搜索的基点，M在有效目标函数f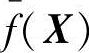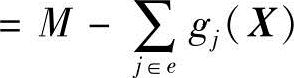中保持不变，而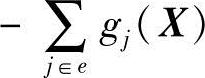的值则随搜索点离约束面的位置而变化。离约束面越近，其值越小；反之，其值越大。这样从不可行离散顶点出发的离散一维搜索实际上是求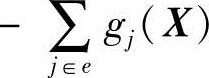的极小值，当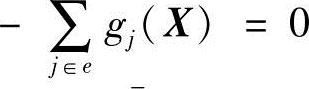，即迸入可行域D，从这时起目标函数f（X）=f（X），由于可行域D的边界好像由M筑起的一堵“高墙”，从而保证始终在可行域内继续搜索f（X）的极小值。按这种处理方法设计的程序可自动地将先由不可行离散点寻找可行离散点和接下来的从可行离散点寻找离散最优点这两个阶段的运算过程很好地统一起来。(www.xing528.com)

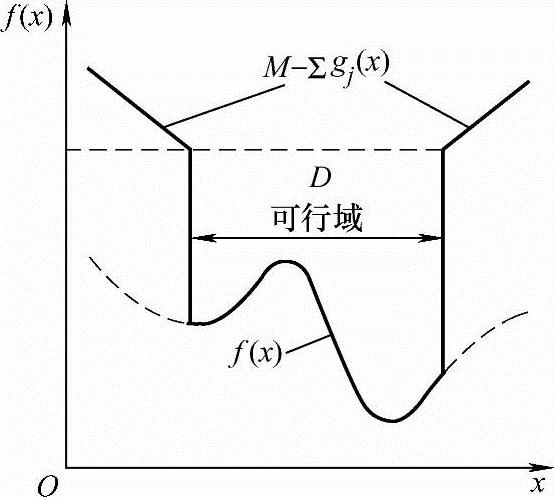
图7-8 有效目标函数图