凑整解法和网格法的比较

该法的特点是先按连续变量方法求得优化解X^*，然后再迸一步找整型量或离散量优化解，这一过程称为整型化或离散化。下面介绍按连续实型量优化得到优化解后如何圆整化、离散化的方法，并讲述其中可能产生的问题。

设有n维优化问题，其实型量最优点为X^*∈rⁿ，它的n个实型分量为x_i^*（i=1，2，…，n），则x_i^*的整数部分（它的偏下一个标准量）［x_i^*]和整数部分加1即［x_i^*]+1（或它的偏上一个标准量）便是最接近x_i^*的两个整型（或离散型）分量。由这些整型分量的不同组合，便构成了最邻近于实型最优点X^*的两个整型分量及相应的一组整型点群［X_i^*]^t（t=1，2，…，2ⁿ，n为变量维数）。该整型点群包含有2ⁿ个设计点，在整型点群中，可能有些点不在可行域内，应将它们剔除。在其余可行域内的若干整型点中选取一个目标函数值最小的点作为最优的整型点给予输出。图7-4所示是二维的例子。在实型量最优点X^*周围的整型点群有A、B、C、D四点，图中B点在域外，A、D、C三点为在域内的整型点群，分别计算其目标函数。由图中等值线可看出，其最优整型点是C点，它即为最优整型设计点［X^*]。但这样做有时不一定行得通，因为连续变量的最优点通常处于约束边界上，在连续变量最优点附近凑整所得的设计点有可能均不在可行域内，如图7-5所示。显然，在这种情况下，采用连续变量优化点附近凑整法就可能得不到一个可行设计方案。另一方面，这种简单的凑整法是基于一种假设，即假设离散变量的最优点是在连续变量最优点附近。然而，这种假设并非总能成立。如图7-6所示，按上述假设，在连续变量最优点X^*附近凑整得到Q点，该点虽是可行点，但并非离散变量的最优点。从图中可见，该问题离散变量最优点应是离X^*较远的P点，而巨目标函数与约束函数的非线性越严重，这种情况越易出现。这些情况表明，凑整法虽然简便，但不一定能得到理想的结果。

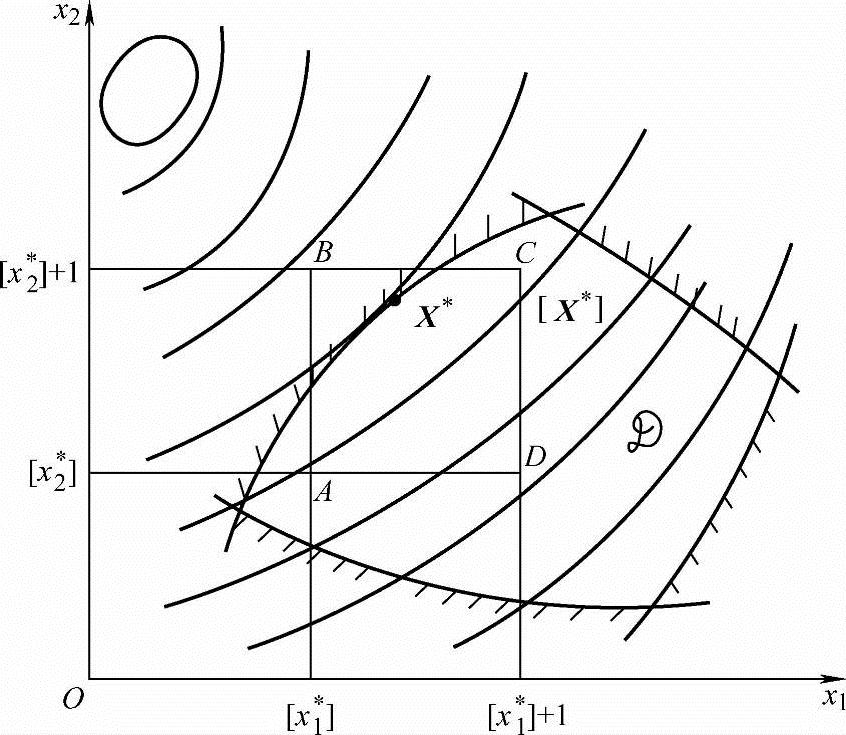
图7-4 X^*周围的整型点群

(www.xing528.com)

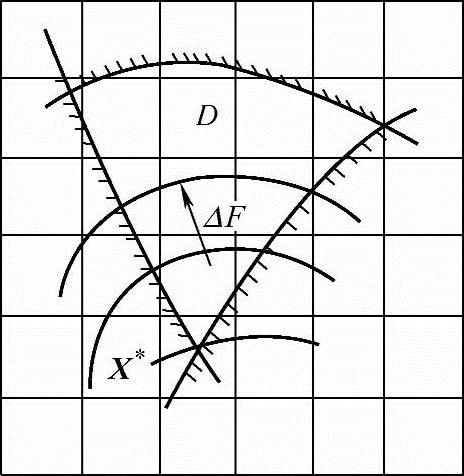
图7-5 X^*周围的整型点群均不在可行域内

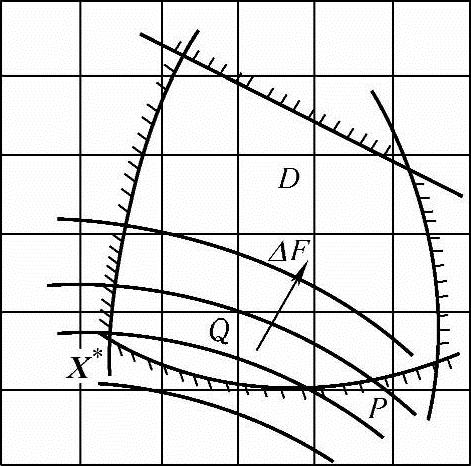
图7-6 离X^*较远处整型点P为优化点的情形

由上述分析可知，离散优化点不一定落在某个约束面上，因此对连续变量约束最优解的K-T条件不再成立。与连续变量优化解一样，离散变量优化解通常也是指局部优化解。我们给出局部离散优化解的定义，是指在此点单位邻域UN（X）内查点未搜索到优于X^*点的离散点，所得的解即为局部离散优化解X^*。当目标函数为凸函数，约束集合为凸集时，此点也是全域的约束离散优化解。